圆弧形底面扁平钢箱梁局部应力分析

饶瑞,黄小峰,林桢楷

(1.广州大学淡江大学工程结构灾害与控制联合研究中心,广东广州510006; 2.华南理工大学土木与交通学院,广东广州510640)

1 工程背景[11]

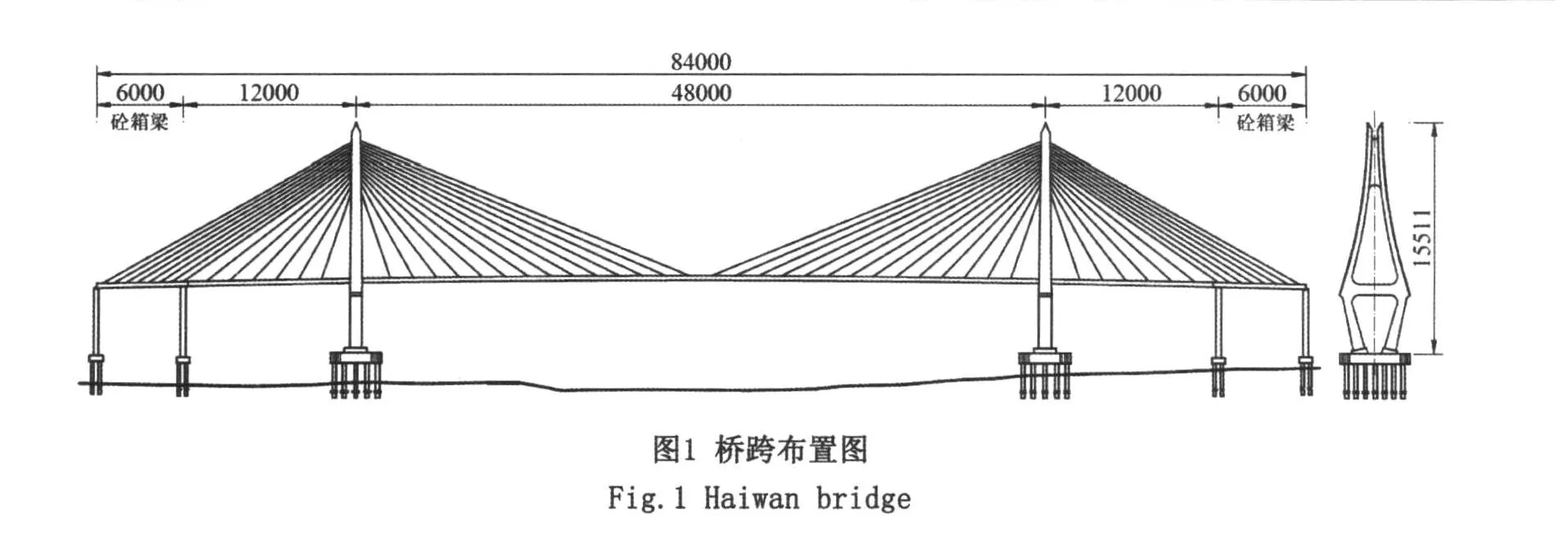
湛江海湾大桥主桥采用双塔空间双索面混合梁斜拉桥,五跨连续半漂浮体系,主跨480m,全长840m,为了改善主塔和主梁的受力性能,边跨设置一个辅助墩,跨径组合为(60+120+480+120+ 60)m,边跨60m为预应力混凝土梁,并伸过辅助墩顶1.8m,主跨及其余边跨为钢箱梁。桥跨布置图如图1所示。

钢主梁为鱼腹式空腹流线型箱梁,底板为圆弧形状,全宽28.5m,中线处梁高3.0m,设两道桁架式纵隔板,除0号段两端和1号段前端设置实体式横隔板外,其余均为桁架式,标准梁段横隔板间距为3.2m。全桥钢箱梁共51块,标准梁段长16m,重约200t,钢梁间采用栓焊连接(内腹板和顶板加劲肋采用高强螺栓连接,其余部分焊接)。典型截面如图2所示。

2 有限元模型

以海湾大桥为工程背景,在ansys平台上建模分析。建模分为整体和局部两个阶段,每个阶段采用不同的尺度进行结构离散。

2.1 整体模型

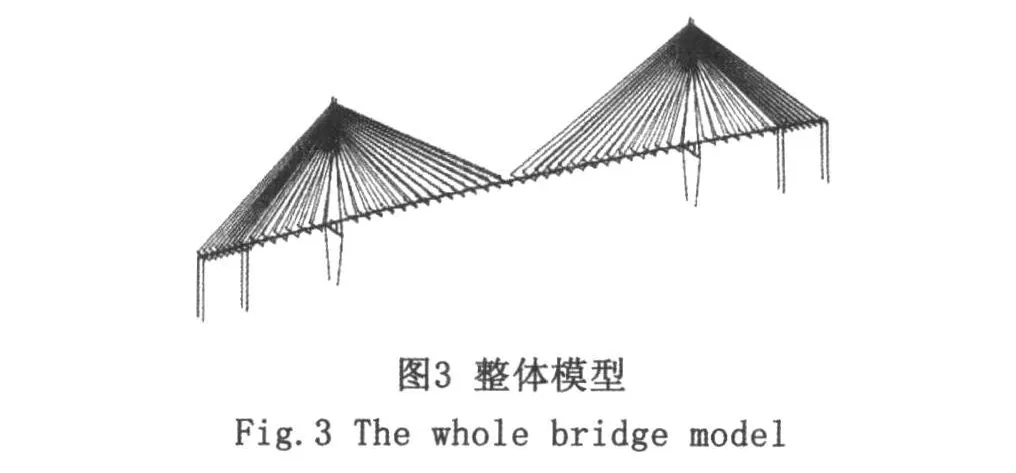
海湾大桥整体模型主要由空间梁单元、桁架单元和只受压的空间杆单元组成。其中,用空间梁单元模拟桥墩、主塔和主梁;用桁架单元模拟斜拉索,斜拉索的垂度效应采用Ernst等效弹性模量进行修正;用只受压空间杆单元模拟施工过程中的支架。另外,考虑到斜拉索锚固点与主梁、主塔形心不重合,在锚固点和主梁、主塔形心之间用刚臂单元连接,以正确反映斜拉索与主梁、主塔的关系。结构共离散为856个单元,1 054个节点。模型示意图如图3。

2.2 局部模型

取三个标准梁端(共长48m)建立局部模型。模型由壳单元和梁单元组成,其中,用壳单元模拟箱梁顶板、底板、外腹板、U肋等板件部分;用空间梁单元模拟由桁架组成的横隔板和纵隔板。为了获得较好的计算结果和收敛速度,在进行单元划分时,严格控制单元形状,尽量采用矩形作为单元的形状,并尽量保证单元节点共面,局部模型离散为112 652个单元,模型示意图如图4。

按照设计图纸,除了墩顶处横隔板采用实体式横隔板外,主梁其他部位的结构形式和尺寸均相同,因此,只要根据实际情况施加合适的边界条件,上述局部模型可用于对除墩顶外的任一主梁梁段进行分析。

根据整体分析结果和静载试验测点的布置情况,本文选取跨中截面(M截面)和墩顶附近截面(D截面,距墩顶3m)进行应力分析。为了叙述方便,将与之对应的模型分别称为M模型和D模型。分析包括恒载及恒载加汽车荷载(最不利荷载位置)两种工况。为了叙述方便,下文称恒载工况为工况一,荷载加汽车荷载工况为工况二。

图5和图6分别给出了工况一作用下M模型和D模型的约束条件和边界内力。至于汽车荷载,则按静载实验的加载情况,用集中力直接加到模型上。汽车荷载具体的加载位置可参阅文献[12]。

[16] Hermina Sutami, “Fungsi dan Kedudukan Bahasa Mandarin di Indonesia”, Paradigma, Vol. 2, No. 2 (2012), pp. 215-216.

2.3 模型的验证

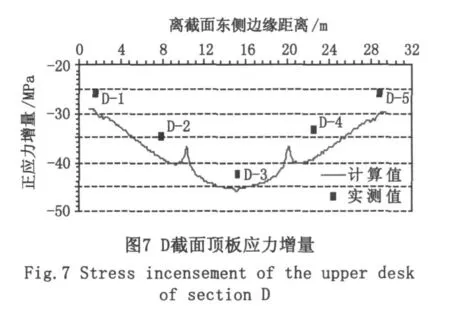
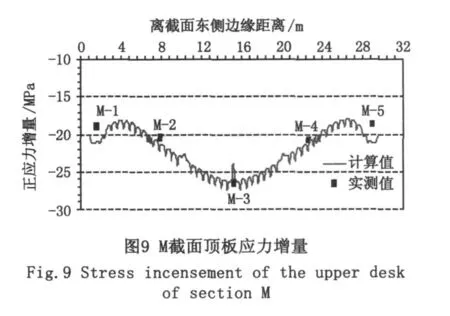
用荷载试验实测值考察模型的可信程度。图7～图10给出了计算值和实测值。从图中可以看出两者吻合良好。可见,所建立的模型能够较好反映桥梁的实际情况,可用于进行桥梁M截面和D截面的顶、底板应力分析。

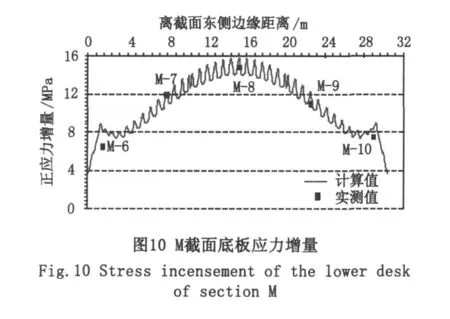
3 顶、底板正应力分析

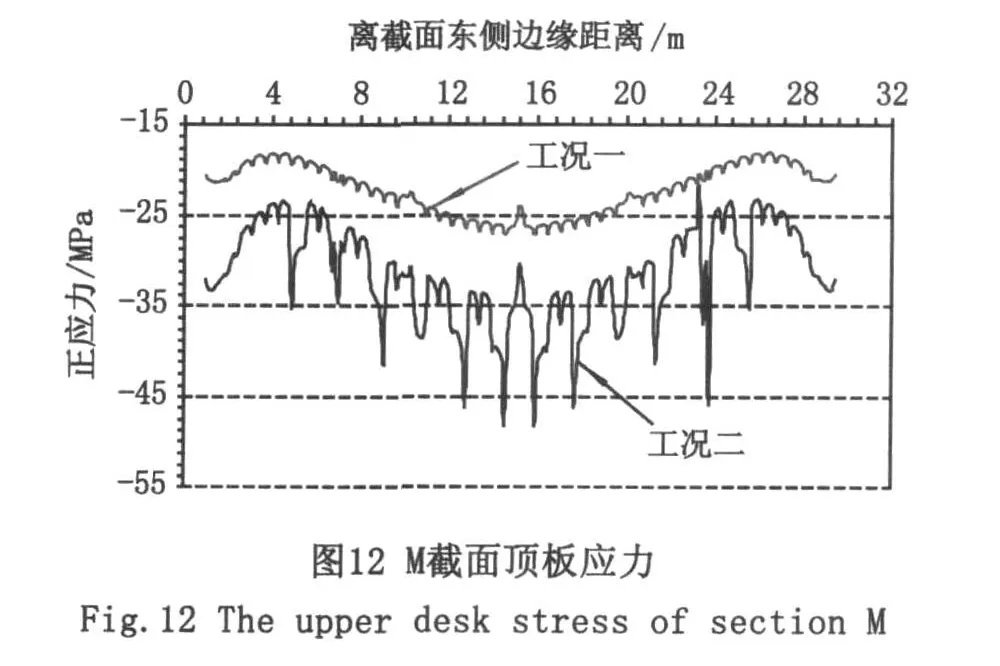
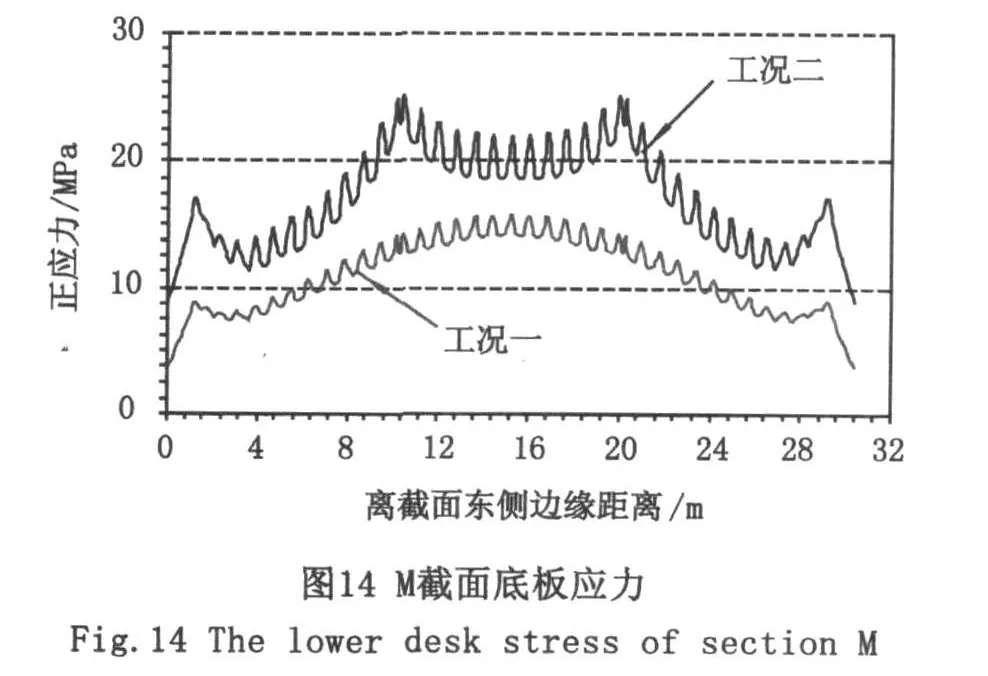
图11～图14给出了M截面和D截面在不同工况作用下顶、底板的正应力分布情况。从图中可以发现：在工况一作用下,各截面顶底板的正应力分布曲线大体呈盆状。截面中部的应力大于截面边缘的应力,其原因主要在于截面横坡的影响。顶、底板中间位置离中性轴的距离比两侧大,因此应力也较大。

同样在工况一作用下,D截面正应力在截面横向三分点附近有明显跳跃,而M截面的正应力沿截面横向波浪式变化。D截面正应力的变化幅度大,而M截面正应力的变化频率高。应力的跳跃变化表明,板件存在明显的剪力滞后。这种剪力滞后,主要是由U肋和桁架式横隔板的产生的。另外,应力曲线表明,不同截面的剪力滞后情况有所不同,其原因可以从截面附近的细部构造和构件的相对刚度两个角度寻找。由于D截面附近有横隔板,受其影响,在桁架节点处产生应力突变,而M截面附近没有横隔板,因此,其应力突变不明显。另一方面,由于支座对板件的约束作用,D截面板件的刚度相对较高,所以U肋对板件应力分布的影响不大,而M截面位于跨中,板件的刚度相对较弱,因此U板件对板件应力分布的影响就凸显出来,使截面的应力沿截面横向波浪式变化。上述分析表明,U肋对跨中截面正应力分布的影响大于对墩顶附近截面应力分布的影响。

在工况二作用下,顶板的正应力曲线有多个明显凸起,应力发生突变的位置基本与车轮荷载施加的位置对应。对于D截面,其顶板正应力最大的变化幅度超过30%,对于M截面,其顶板正应力的增幅超过80%。

在工况二作用下,底板正应力曲线的趋势与工况一的基本一致,但变化幅度增大,尤其是M截面,其应力变化幅度增大更加明显。

4 不同截面形式钢箱梁正应力比较

文献[8]和文献[10]分别以润扬大桥北汊桥和苏通大桥为工程背景,分析了折线形底板扁平钢箱梁的应力分布情况。结果表明,这种类型的钢箱梁应力分布并不均匀。而上述的分析表明圆弧形底面扁平钢箱梁截面的正应力同样存在分布不均匀的特点。可见,应力分布不均匀是两种底板形式扁平钢箱梁正应力分布的共性。底板形式并不能从根本上改变正应力分布的特点。

由于几个箱梁在尺寸上、荷载上均有所不同,因此在应力量值上进行对比并无实际意义。因此,下面将从跨中截面在最不利荷载作用下应力分布的不均匀程度这个角度对两种底板形式钢箱梁应力作进一步比较。考虑到两种形式钢箱梁的主要差别在于其底板形式,在此,仅对其底板正应力进行对比。

参照剪力滞系数的定义,定义应力不均匀性系数为

式中σmax—箱梁节点应力最大值—整个箱梁截面的应力平均值。

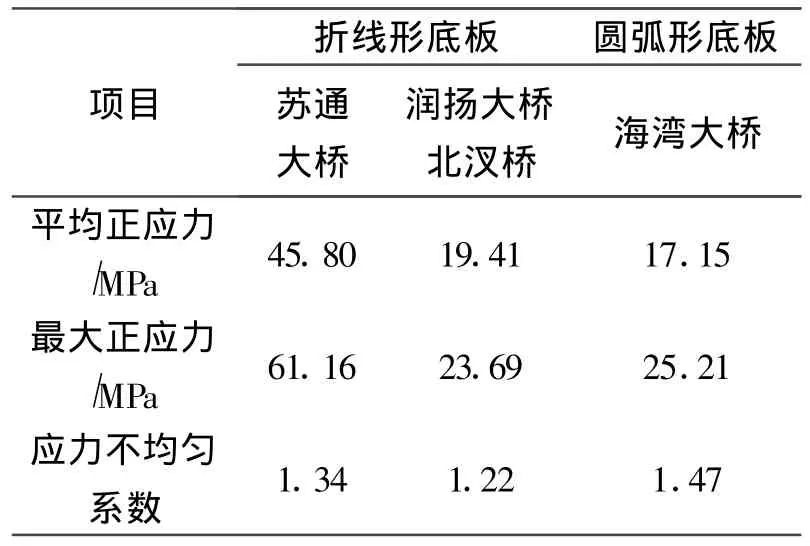
表1 应力不均匀系数Tab.1 Non-uniform coefficient of normal stress

应力不均匀系数可用来量化应力分布的不均匀程度。按照式(1),可计算出润扬大桥北汊桥、苏通大桥和海湾大桥跨中截面底板在最不利荷载作用下的正应力不均匀系数。结果列于表1。

从表中可以发现,圆弧形底板扁平钢箱梁的底板应力不均匀程度略大于折线形扁平钢箱梁。这一点在设计时必须引起注意。

5 结论

1)在荷载作用下,钢箱梁截面的顶、底板都出现剪力滞现象。

2)U肋对跨中截面应力分布的影响大于对墩顶截面的影响。

3)在车辆荷载作用下,顶板的正应力曲线有多个明显凸起,应力发生突变的位置基本与车轮荷载施加的位置对应;底板正应力的分布趋势没有改变,但变化幅度明显增大。

4)采用圆弧形底板和折线形底板的扁平钢箱梁顶底板都存在应力分布不均匀的特点,底板形式并不能从根本上改变应力分布的特点。相比之下,圆弧形底面钢箱梁的底板正应力不均匀程度略大于折线形底面钢箱梁。

[1]FAN Z F.Behavior of steel box girderswith top flange bracing[J].Joumal of Structural Engineerig,1999,125(8)：829 -837.

[2]CHANG P C,FLATAU A,LIU S C.Review paper：health monitoring of civil infrastructure[J].Structural HealthMonitoring,2003,2(3)：257-267.

[3]REN W X,PENG X L.Baseline finite element modeling of a large span cable-stayed bridge through field vibration tests [J].Computers and Structures,2005,83(8/9)：536-550.

[4](日)小西一郎.钢桥(第一分册)[M].北京：人民交通出版社,1980.

[5]钱冬生,陈仁福.大跨悬索桥的设计与施工[M].成都：西南交通大学出版,1999.

[6]徐伟,李智,张肖宁.子模型法在大跨径混凝土斜拉桥桥面结构分析中的应用[J].土木工程学报,2004,37 (6)：30-34.

[7]王浩,李爱群,赵大亮,等.润扬悬索桥钢箱梁受力分析及实验研究[J].哈尔滨工业大学学报,2006,38(7)：1062-1064.

[8]丁幼亮,李爱群,赵大亮.润扬大桥北汊斜拉桥钢箱梁的局部应力测试与分析研究[J].工程力学,2006,23 (12)：123-128.

[9]刘毅,李爱群,丁幼亮,等.润扬悬索桥扁平钢箱梁局部应力的测试与分析[J].东南大学学报(自然科学版),2007,37(3)：275-279.

[10]张鹏飞,张启伟.千米级斜拉桥扁平钢箱梁的局部力学行为[J].天津大学学报,2010,43(7)：592-600.

[11]徐金勇.大跨度混合梁斜桥弹塑性极限承载力及施工控制研究[D].广州：华南理工大学,2007.

[12]广东省交通运输建设工程质量检测中心.湛江海湾大桥动静载报告[R].2007.