基于非线性序转换的层次分析模型

庞彦军,刘立民,马丽涛,刘开第

(河北工程大学理学院,河北邯郸056038)

层次分析法(analytic hierarchy process,AHP)[1]是Saaty教授在二十世纪七十年代末提出的一种无结构化决策方法,被广泛应用于涉及指标重要性权重的众多应用领域[2-5]。AHP采用“两两比较”的方法,在准则下对准则支配的相邻下层各项指标通过构造比例标度判断矩阵,并利用基于“一致性”检验的特征向量法(或幂法,或和法)对下层指标排序,很好地解决了相邻两层指标间的排序问题[6-7]。

然而对于三层及以上层次结构,需要在顶层目标下对底层指标按重要性大小排序,则必须解决以下两个问题：一是在上层每一项指标下对该指标所支配的相邻下层指标排序;二是通过序关系转换在顶层目标下对底层指标排序。AHP实现序转换的方法为线性序转换,这种方法仅适用于简单递阶层次结构,当递阶层次结构为复杂结构时,线性序转换只能作为真实序转换的一种近似。

本文分析递阶层次结构的复杂性,将排序度量映射到高维状态空间上,提出了复杂层次结构序关系转换的非线性方法,给出了递阶层次结构指标排序的一般方法。

1 递阶层次结构的类型

递阶层次结构的复杂性由上、下层指标间的不同联接方式决定,分为简单层次结构及复杂层次结构(图1)。

简单层次结构的特点是,每一项底层指标发生时,影响且只影响相邻上层中一项指标。只通过一项指标传递到目标G的序关系,是且只能是线性关系,对应线性序转换。

复杂层次结构的特点是,当一项底层指标发生时,会同时影响相邻上层至少两项指标,此时,经中间指标B1,B2,B3,传递到G的序关系就不再是线性关系,而是非线性序关系,对应序转换是非线性转换。

2 复杂层次结构的非线性序转换算法

以三层复杂结构为例。

设由AHP法已求得底层n项指标关于中间层指标j(j=1-m)的排序向量

及m项中间层指标关于顶层目标G的排序向量

求在目标G下对底层n项指标排序。

2.1 难点分析

当底层指标i发生时,目标G同时接收到中间层m项指标B1～Bm发送的关于指标i的m种信息μi(j)(j=1～m),但是,无法得知每一个μi (j)究竟对目标G提供了多少关于指标i的“有效信息”,也无法得知这m种信息按着怎样的“规律”融合。所以,通过某种线性运算得出指标i关于目标G的排序度量αi(G)仅是真实度量的一种近似。

本文通过把排序度量 μi(j)映射到能描述 μi(j)“重要性程度”的高维状态空间上,分析 μi(j)在每个子空间上的映射值究竟对目标G提供了多少关于指标i的“有效信息”,并通过“信息融合”探索非线性序转换的算法途径。

2.2 排序度量到高维状态空间的映射

步骤1：将指标i对指标j的影响程度μi(j)划分为s=5个等级,设{F1,F2,…,F5}是状态空间F的一种划分,满足

Fi∩Fj=φ(i≠j)且∪5k=1Fk=F称Fk(k=1～5)是第k种状态,也称为第k类。

步骤2：令a=min{μi(j)},b=max{μi(j)},将区间[a,b]四等分,连同区间端点在内的5个分点是a=a1＜a2＜a3＜a4＜a5=b在[a,b]上,以ak(k=1～5)作为F6-k类的标杆值。构造5个等级的标准隶属函数α1(t)～α5(t),如图2所示。

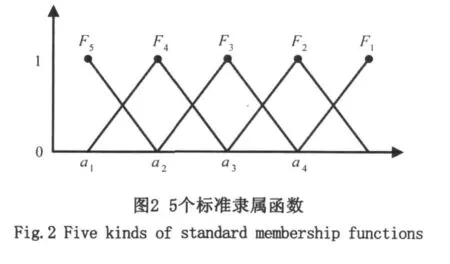
图2中,F1类的隶属函数 α1(t)由折线a1a4F1表示;F2类的隶属函数 α2(t)由折线a1a3F2a5表示;F3类的隶属函数 α3(t)由折线a1a2a3F4a5表示;F4类的隶属函数α4(t)由折线a1F4a3a5表示;F5类的的隶属函数 α5(t)由折线F2a2a5表示。

根据图2的5个隶属函数,任一排序度量 μi(j)可表为一个5维向量：

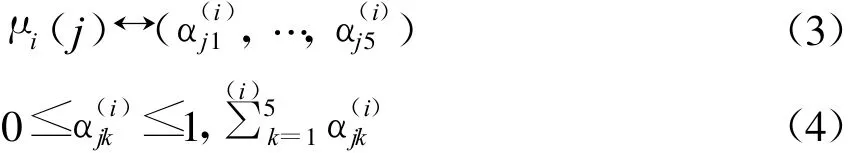
其中,α(i)jk—指标j的k类隶属度,表示指标i发生时对指标j的影响属于Fk类的隶属度。

2.3 隶属度非线性转换的算法步骤[8]

隶属度的非线性转换是在指标隶属度中包含着对目标分类不起作用的冗余值,而清除冗余值的过程是非线性计算过程。

设指标j关于目标G的重要性权重为λj(G),目标G的状态转移矩阵为U(i)(G)=()m×5。求指标i发生时对目标G的影响属于Fk类的隶属度(G)(k=1～5)。

令

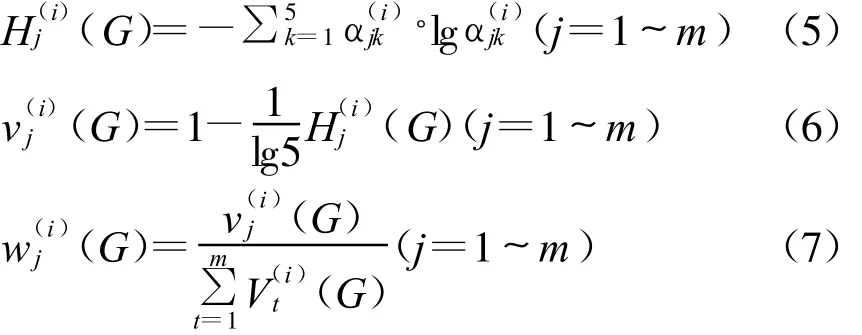
步骤1：计算指标j的k类有效值

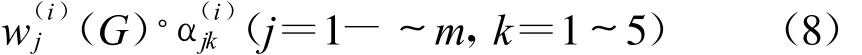
步骤2：计算指标j的k类可比值

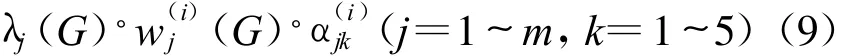
步骤3：计算目标G的k类可比和

步骤4：计算目标G属于Fk类的隶属度

2.4 基于隶属度的排序方法

令F1～F5的量化值依次为9,7,5,3,1,称

指标i对目标G的影响度。可按n(i)(G)的大小,在目标G下对指标i排序。

3 算例分析

某矿10号污水坝设计为一粘土斜墙防渗土石坝,建成蓄水后出现渗漏。根据场区工程地质和水文地质条件,拟采用4种防渗加固方案：P1是粘土铺盖+静压注浆;P2是深层搅拌桩;P3是高压摆喷+静压注浆;P4是深孔注浆。

有6种衡量方案优、劣的指标：I1是治理可靠性,I2是安全性,I3是工程投资,I4是施工工期,I5是施工难易程度,I6是环境影响。这样,方案排序构成一个三层递阶层次结构(图3),G为总目标。

显然图3所示是一个复杂结构,对应非线性序关系转换。

在给定各方案关于6种指标的逻辑评语集后,文献[9]用层次分析法确定了中间层指标I1～I6关于目标目标G的重要性权重向量

及4种方案关于6种指标的排序度量矩阵：其中,U(G)4×6的第j列元素为各方案关于中间指标Ij的排序度量。

方案排序步骤如下：

步骤1：构造排序度量的隶属函数

步骤2：构建标准隶属函数

以P1为例,P1关于6种指标的排序度量,构成目标G关于P1的状态转移矩阵U(1)(G)：

步骤3：计算隶属度向量

根据目标 G关于P1的状态转移矩阵 U(1)(G),得P1对G影响的隶属度向量为：

同理得方案P2,P3,P4对G影响的隶属度向量为

步骤4：计算影响度

取F1～F4的量化值依次为4,3,2,1,各方案的影响度分别为

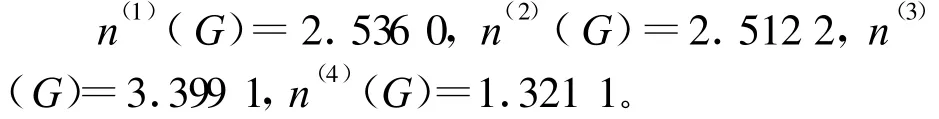
因为n(3)(G)＞n(1)(G)＞n(2)(G)＞n(4)(G),所以,方案P3最优,P1、P2次之,P4最差。

4 结语

递阶层次结构中方案排序问题的本质是实现非线性序转换。通过把“排序度量”映射到高维状态空间上,并利用区分权滤波算法实现了高维空间上隶属度向量间的非线性转换,可以作为解决复杂层次结构中方案排序的一种实用方法。

[1]许树柏.层次分析法原理[M].天津：天津大学出版社,1998.

[2]郑贤斌,陈国明.基于FTA油气长输管道失效的模糊综合评价方法研究[J].系统工程理论与实践,2005, 25(2)：139-144.

[3]易俊,伍建林,史佩,等.二级模糊安全评估方法及其在油库安全中的应用[J].中国安全科学学报,2007, 17(6)：135-139.

[4]SAATTY T L.Decision making with the analytic hierarchy process[J].International Journal of Services Sciences, 2008,1(1)：83-98.

[5]戴佑斌,张尚根,周早生,等.模糊一致矩阵理论在地铁深基坑支护方案优选中的应用[J].岩土工程学报,2005,27(10)：1162-1165

[6]周书敬,朱志,王飞.基于灰色层次分析的房地产投资决策[J].河北工程大学学报(自然科学版),2010, 27(2)：83-86.

[7]李树文,李少雄,刘嘉玮,等.水质模糊综合评价模型的改进[J].河北工程大学学报(自然科学版),2009, 26(3)：102-105.

[8]庞彦军,周少玲,杨 珠,等.水质模糊综合评价模型的改进[J].河北工程大学学报(自然科学版),2007,24 (3)：89-93.

[9]陈永贵,邹银生,张可能.坝基防渗治理的多目标模糊决策方法[J].湖南大学学报,2008,35(3)：15-18.