基于模糊数学和粒子群算法的边坡参数反分析*

孙志彬 杨小礼 黄阜

(中南大学土木工程学院，湖南长沙410075)

边坡是道路与铁路工程中常见的构筑物形式之一，无论是对原有边坡进行处治，还是利用现有材料构建边坡以满足人们生产与生活的需要，都必须进行边坡的稳定性分析.而不管采用何种方法进行边坡稳定性分析，边坡的力学强度参数都非常重要.但由于边坡内部岩土体结构复杂，内部强度随空间变化较大，参数获取较为困难.而模型试验存在取样困难、尺寸效应等问题.实测坡体位移比较简便，因而采用位移反分析方法计算岩土体强度参数已经成为一种理想的岩土参数确定方法.

自Kavanagh等［1］提出反演弹性固体弹性模量的有限元方法以来，国内外学者对参数反演做了大量的研究.从最初的逆解法［2］、图解法［3］逐渐发展为建立目标函数并求出最优解的优化法.优化法发展的初期，常常采用基于梯度的各种算法，如单纯形法［4］、罚函数法［5］.随着智能技术的逐渐发展，众多学者将各种智能算法与优化法结合起来，用来寻找目标函数的最优解.常用的智能算法有小波向量机［6］、模拟退火算法［7］与遗传算法［8］，或者将不同的智能算法结合起来，以弥补它们各自的不足［9］.

由优化法的求解过程可知，影响优化法求解的因素有两种，即目标函数的构造和求解.大多数学者对优化法的研究集中在对目标函数的求解方法上，即如何利用更少的步骤求解出更精确的解，对目标函数的构造则研究较少.文中以浙江某滑坡为例，将模糊数学与粒子群算法结合起来，构造了一种新的参数反演的目标函数，并计算了该函数对边坡土体强度参数的敏感度，从而为确定岩土边坡强度参数开辟了新的思路.

1 目标函数的构造

1.1 传统方法

利用优化法反演土体力学参数，需要构建目标函数，该函数通常为测点处位移实测值与计算值的平方和，即

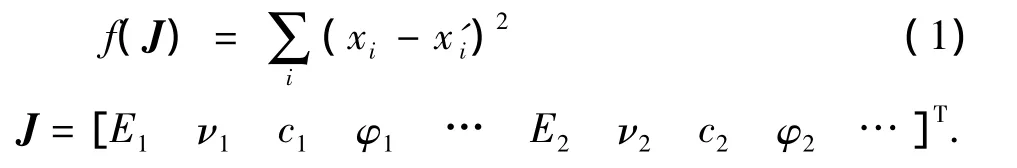
式中:xi为第i个测点的实测位移值;x'i为第i个测点的计算位移值;J为待反算的边坡强度参数矩阵.Ei、νi、ci、φi表示不同部分土体的强度参数，分别为弹性模量、泊松比、黏聚力、内摩擦角.

由公式(1)可知，随着矩阵J中强度参数的变化，函数f也相应地变化.据此不断调整J中的参数，使

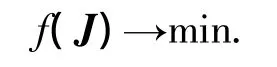
此时矩阵J中的强度参数即为反算的结果.

传统的观测边坡位移方式有两种:一种是利用全站仪观测边坡表面若干测点的位移，如图1(a)所示;另一种是利用测斜仪等仪器监测边坡内部若干测点的位移，如图1(b)所示.

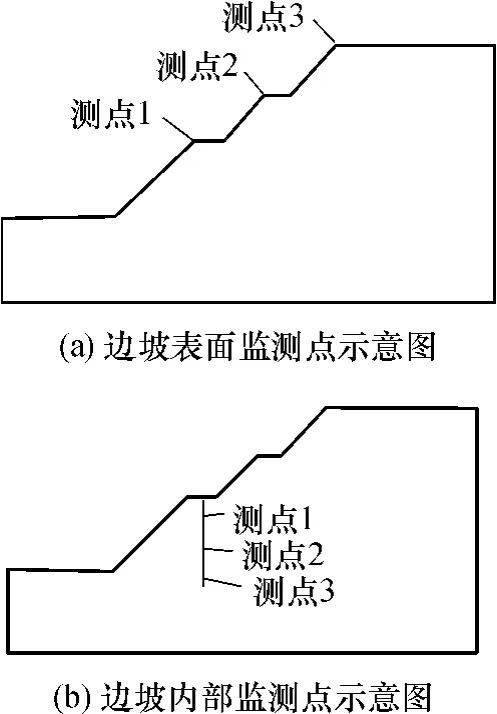
图1 边坡测点位置Fig.1 Locations of the measuring points of slope

边坡表面的位移影响因素较多，例如边坡表面的土体崩落、雨水冲刷等.内部位移监测不仅可以有效减少干扰，还可对发生大规模滑坡前边坡的内部滑动进行观测.

数值分析结果表明，边坡内部滑动面附近土体的剪应变最大.大量的观测资料也表明，在滑坡发生前，滑动面附近的土体已经发生移动.虽然滑面土体范围不大，但随着时间的推移，其上部的土体将沿着滑面土体发生整体滑移，从而发生滑坡.因此滑动面附近土体对整个边坡的稳定性起控制作用.但在发生大规模滑坡之前，该部分土体的位移从宏观上看并不十分显著.在边坡参数反分析的过程中，该土体内部的测点的计算和实测位移差对式(1)中构造的优化函数f(J)的影响较小，甚至在误差范围内，很难对反算出的边坡位移函数造成影响.由此可见，传统方法将边坡各测点位移差的平方和作为目标函数，忽略了在边坡滑移过程中各部分土体性质的不同，无法精确地反演出边坡的强度参数.

1.2 新的目标函数构造思路

由于边坡内部土体变形与滑动性质的不同，将各测点位移以相同的权值进行计算存在不足之处.根据滑动特征，边坡内部土体可分为3类:滑坡床、滑坡面和滑坡体.新的目标函数根据测点所在的位置，将其位移乘以加权系数代入式(1)，得式(2):

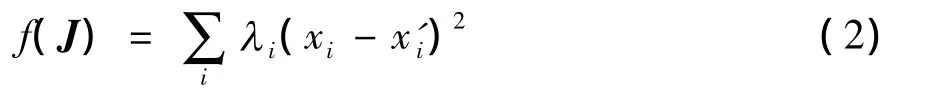
式中，λi为加权系数.为了确定某一测点位移的加权系数，需要确定该测点属于哪部分的土体.但实际上，边坡土体的精确划分存在困难，因为各部分土体之间的界限是模糊的，在发生大规模滑动之前，滑坡体与滑坡面之间、滑坡面与滑坡床之间的转换在空间上是渐变的.尤其对于“交界面”附近的土体，在性质上很难单独划分为某一类别的土体，往往“兼而有之”两种土体的性质.可以利用模糊数学对土体的这种性质进行描述.据文献［10］，可根据边坡的内部位移监测数据寻找潜在滑动面，也可利用地质钻孔资料，根据钻出物的性质判断潜在滑动面的位置.

设某一测孔深度为h1，滑动面深为h2.隶属函数是以测点深度为自变量的线性函数.土体的隶属度函数U由子函数μ1、μ2、μ3组成，分别表示该土体对滑坡床、滑坡面与滑坡体的隶属度，如下所示:

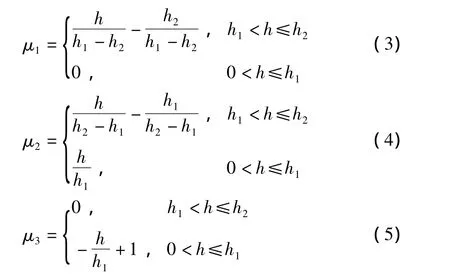
式中:h为该测点的深度.

由函数U可知，当测点分别位于滑坡表面、滑动面和基岩表面时，其对滑坡床、滑坡面和滑坡体3种土体的隶属度为1.离上述3点的距离愈远，其对相对土体的隶属度愈小，隶属度与距离呈线性关系，函数曲线如图2所示.

由式(1)及隶属度函数U可知，边坡力学参数反分析的优化法的目标函数权重可表示为

目标函数为

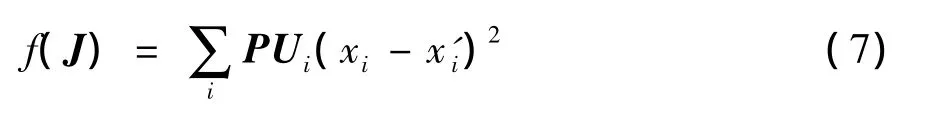
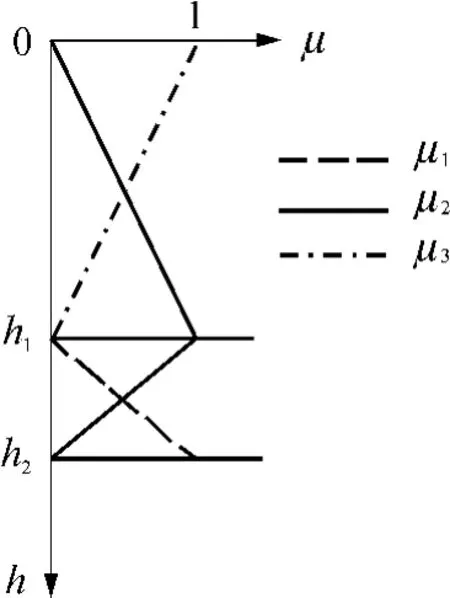
图2 隶属度函数曲线Fig.2 Membership function curve

式中:P为滑坡床、滑坡体与滑坡面的权重系数矩阵，P=［η1η2η3］，η1、η2、η3分别表示3类土体的位移在反分析过程中的权重系数;Ui为某测点的隶属度矩阵，Ui=［μi1μi2μi3］，μi1、μi2、μi3分别表示第i个测点对3类土体的隶属度.

欲构造目标函数，除根据测点位置计算其隶属度外，还需求取不同土体的位移权重系数，即矩阵P.由于滑动面附近的土体发生剪切破坏，对于一些尚未发生明显滑移的边坡，潜在滑动面附近土体的剪切位移可以表征滑坡的状况.同样，在相同尺寸的计算模型中，不同的强度参数取值也将影响该部分土体的剪切位移，所以理想的矩阵P满足以下两个条件:一是体现不同土体在滑坡过程中的作用，一般情况下为滑坡面＞滑坡体＞滑坡床;二是使各测点的位移乘以加权系数后对滑动面的位移有足够大的敏感性.

现以浙江某滑坡为例，利用粒子群算法说明矩阵P的构造思路.该边坡为土石混合体边坡，边坡形状与测点布置如图3所示，每个测斜孔长15.0m，每0.5m取一个测点，各个测点的位移如图4所示.

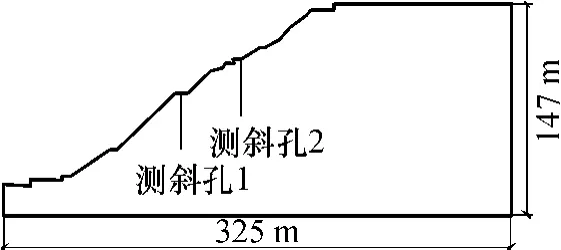
图3 边坡形状及测点位置Fig.3 Slope shape and location of measuring points

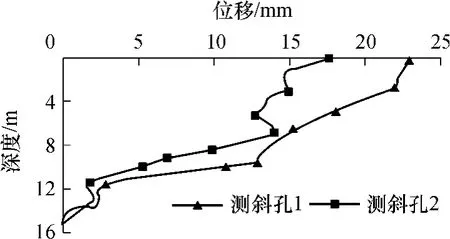
图4 监测点的实际位移Fig.4 Actual displacements of monitoring points

式中，x'j(P)为加权后的测点位移，x'ij为数值计算得出的各测点位移，j为计算次数.为了保证边坡各测点位移对滑动面的剪切位移的敏感性，要求

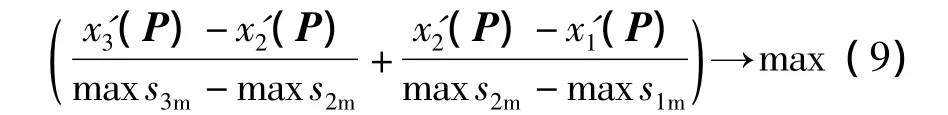
式中，x'1(P)、x'2(P)、x'3(P)分别为强度参数为时的测点位移值，maxs1m、maxs2m、maxs3m为相应强度条件下的边坡最大剪切位移值.

若考虑不同类别土体在滑坡过程中的重要性:

上述问题即为在满足式(10)的条件下求式(9)，可采用粒子群搜索算法.粒子群算法［11-12］是一种基于群体方法的演化计算技术，模仿一群飞鸟在一定区域中搜索食物的方法.鸟群的搜索空间对应于设计变量的变化范围，食物对应于适应度函数的最优解.每个优化问题的潜在解对应于搜索空间中的一个粒子，每个粒子都有自己的位置和速度(决定飞行的方向和距离)，还有一个由被优化函数决定的适应值.各个粒子记忆、追随当前的最优粒子，在解空间中搜索.每次迭代的过程不是完全随机的，如果找到较好的解，将会以此为依据寻找下一个解.

在本问题中，粒子种群规模为10，最大迭代次数为15，其他参数取为惯性权重w=0.9，学习因子e1=e2=2.在计算过程中，若某个粒子的一个以上的分量的取值超过解空间的范围，则不计算其适应度，并且失去同别的粒子竞争最优位置的机会，直至其被重新吸引至解空间的范围内.

经过15次迭代以后，求得矩阵

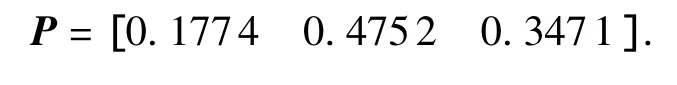
2 目标函数对强度参数的敏感性分析

为了验证新的目标函数对所要反演的边坡强度参数的敏感性，文中特别计算了图3所示的边坡参数改变时的目标函数值(见表1和2)，并做出了目标函数对参数的敏感度曲线.为便于比较，同时计算出按传统的优化方法反分析所构造的目标函数的函数值，并绘出敏感度曲线，结果如图5所示.

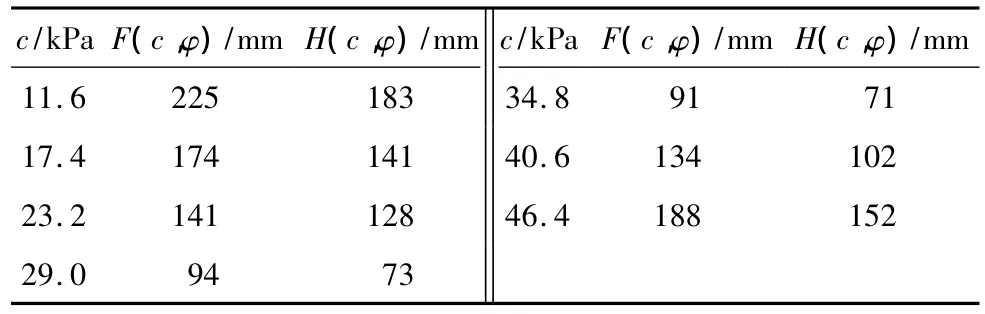
表1 c值改变时目标函数的变化值Table 1 Objective function values varying withc

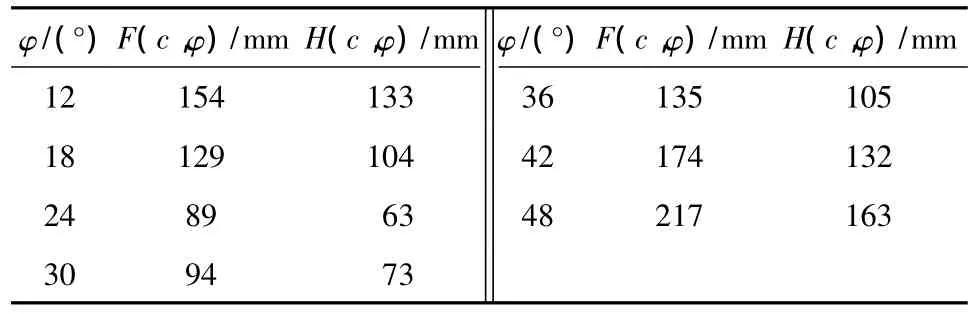
表2 φ值改变时目标函数的变化值Table 2 Objective function values varying withφ

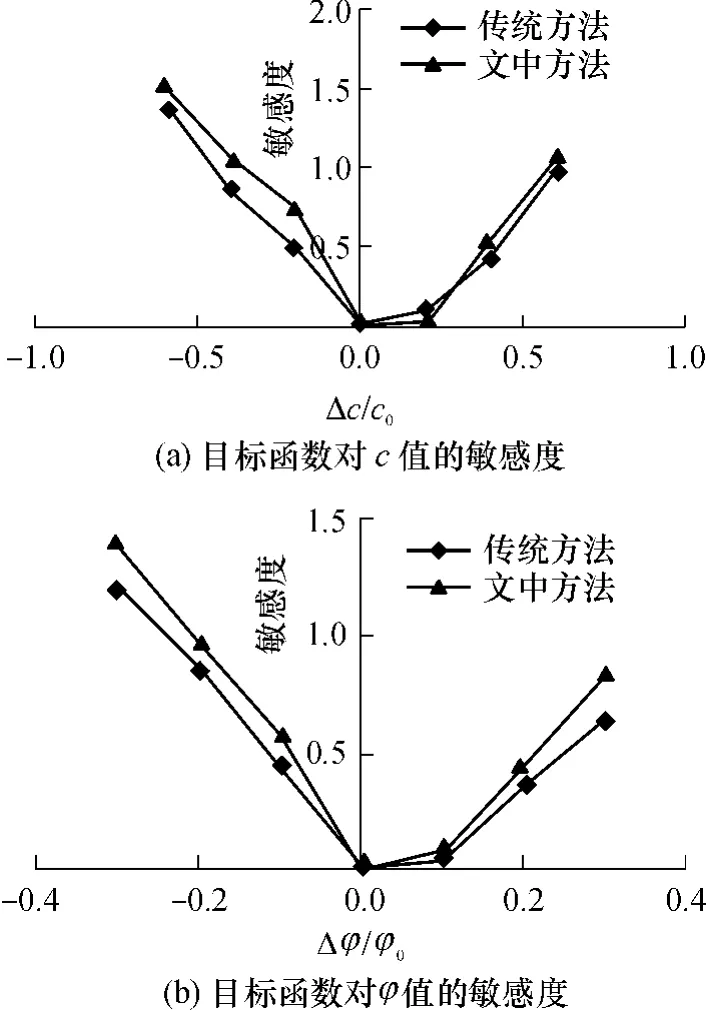
图5 目标函数对c值和φ值的敏感度Fig.5 Sensitivity of objective function to c and φ

表1和2中，边坡强度参数的设计值为c= 29kPa、φ=30°，设F(J)为传统目标函数，H(J)为新的优化法目标函数，为了便于说明，只反演参数矩阵中的黏聚力与内摩擦角值.F(J)与H(J)可写为F(c，φ)和H(c，φ).分别计算目标函数对c与φ敏感度变化.

目标函数对c的敏感度定义为

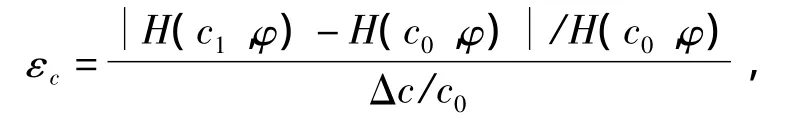
敏感性分析结果表明，边坡位移对c的敏感度要大于对φ的敏感度.就两个目标函数而言，无论是对于c还是φ，文中提出的目标函数的敏感度大多数情况下大于传统方法的敏感度.这说明在利用优化法进行边坡强度参数反分析时，文中的方法具有优势.利用目标函数进行求解，得目标边坡的强度参数为c=30.5kPa，φ=31.3°.

文中提出的算例为单一滑动面的边坡，对于多层土体且仅有单个滑动面的边坡，亦可以使用文中提出的方法.但若边坡有若干次生滑动面，则需要重新考虑各个测点的隶属度计算方法.

3 结语

传统边坡参数反分析的目标函数忽视各测点的位置与位移状态，没有反映边坡的内部位移情况.因此，文中利用边坡内部的监测资料，对边坡位移进行加权后再构造目标函数.研究发现通过新的目标函数可以有效地求解边坡的强度参数.层状土质边坡存在土层厚度不同造成的尺寸效应，利用文中提出的方法存在一定的局限性，在构建目标函数时，可以寻找一个与土层厚度无关的位移量.

［1］ Kavanagh K，Clough R.Finite element applications in the characterization of elastic solids［J］.International Journal of Solids and Structures，1971，7(1):11-23.

［2］ Sakurai S，Takeuchi K.Back analysis of measure displacement of tunnel［J］.Rock Mechanics and Rock Engeering，1983，16(3):173-180.

［3］ 杨林德.岩土工程问题的反演理论与工程实践［M］.北京:科学出版社，1996:120-123.

［4］ Gioda G.Problem in elastic-plasticity identification of cohesion，friction angle and in-situ stress by pressure tunnel tests［J］.International Journal for Numerical Methods in Engineering，1980，15(5):1823-1834.

［5］ 王华宁，吕爱钟.巷道裂隙岩体的损伤参数辨识［J］.岩土工程学报，2001，23(5):593-597.Wang Hua-ning，Lü Ai-zhong.Damage parameter identification of joint rock mass in underground opening［J］.Chinese Journal of Geotechnical Engineering，2001，23 (5):593-597.

［6］ 王复明，李晓龙，苗丽，等.基于小波支持向量机的围岩力学参数辨识［J］.水力发电学报，2010，6(3):184-190.Wang Fu-ming，Li Xiao-long，Miao Li，et al.Mechanical parameters identification of surrounding rock based on wavelet SVM［J］.Journal of Hydroelectric Engineering，2010，6(3):184-190.

［7］ 魏连伟.基于模拟退火算法的水文地质参数识别［J］.天津大学学报，2003，36(5):618-621.Wei Lian-wei.Hydrogeological parameter identification on the simulated annealing genetic algorithm［J］.Journal of Tianjin University，2003，36(5):618-621.

［8］ 高玮，郑颖人.基于遗传算法的岩土本构模型辨识［J］.岩石力学与工程学报，2002，21(1):9-12.Gao Wei，Zheng Ying-ren.Identification of the geomaterial constitutive model based on genetic algorithm［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21(1):9-12.

［9］ 刘鹏程，纪晨.改进模拟退火－单纯形综合反演方法［J］.地球物理学报，1995，38(2):199-205.Liu Peng-cheng，Ji Chen.An improved simulated annealing-downhill simplex hybrid global inverse algorithm［J］.Chinese Journal of Geophysics，1995，38(2):199-205.

［10］ 孙志彬，杨小礼.基于深部位移的边坡滑动特征分析［J］.长沙理工大学学报:自然科学版，2010，7(2):43-47.Sun Zhi-bin，Yang Xiao-li.Sliding characteristics analysis of land slide based on the deep displacement［J］.Journal of Changsha University of Science and Technology:Natural Science，2010，7(2):43-47.

［11］ Kennedy J，Eberhart R C.Proceedings of IEEE international conference on neural network［C］.New York: IEEE Press，1995:1942-1948.

［12］ 高玮.基于粒子群优化的岩土工程反分析研究［J］.岩土力学，2006，27(5):795-798.Gao Wei.Back analysis algorithm in geotechnical engineering based on particle swarm optimization［J］.Rock and Soil Mechanics，2006，27(5):795-798.