低矮房屋标准模型的风洞试验研究*

谢壮宁 刘帅 石碧青

(1.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640;

2.东莞电力设计院，广东东莞523009;3.汕头大学土木系，广东汕头515063)

历次风灾调查结果显示，极端风环境下被破坏的主要对象是低矮房屋［1］.风工程界在最近30年里进行了大量低矮建筑风荷载特性的研究，其中包括几个建筑原型在真实风环境下的场地风压测量试验.最典型和影响最大的是美国德克萨斯理工大学(TTU)的足尺标准模型［2］，它是TTU风工程研究现场实验室(WERFL)在空旷场地上建造的一个永久性金属建筑模型，可根据实际需要进行360°转动，模型表面布置有若干风压测点，旁边设置有气象观测塔用于测定风速和风向［3-4］，该模型事实上已经成为目前国际公认的、较为权威的一种评估建筑风洞模拟技术的标准模型，简称TTU标模.针对低矮房屋的很多基础性风工程研究文献均是以TTU标模作为研究对象，如文献［5］中采用风洞试验方法研究了不同开口方式下TTU的内外压力变化及其频域相干特性.

以往研究表明［6-9］，足尺/缩尺模型试验的对比结果中，平均风压系数基本上是令人满意的，但在极值吸力起主导作用的区域上，足尺/缩尺模型上的脉动风压系数却存在较大的差异，这些极值常常很明显地出现在斜风下有流体分离、再附出现的靠近屋角的屋面区域、屋面迎风边缘区域和屋脊等处.目前，仍然没有完全建立预测建筑结构表面这些关键区域极值吸力的精确风洞模拟技术.

文中针对3种不同缩尺比的TTU试验模型，研究了同一流场内模型尺寸变化对风洞试验结果的影响;同时将1∶30模型在3种流场中的试验结果分别与实测数据以及其它风洞试验数据进行对比，来验证所用风洞对低矮建筑模型试验结果的可靠程度.通过对比确定可用于低矮房屋风洞试验的风场，从而为后续低矮房屋风洞试验研究提供基础技术保障.

1 TTU标模的风洞试验

1.1 风洞试验设备及流场模拟

风洞试验在汕头大学大气边界层风洞(STDX-1)中进行，该风洞是一座全钢结构的闭口回流式矩形截面风洞，主试验段宽3m、高2m、长20m，风速连续可调，最大风速可达45 m/s.测压采用美国Scanivalve公司的DSM3200系统，试验采样频率为312.5Hz，样本长度为20480.试验中采用被动模拟方式在该风洞中调试了3种流场:(1)流场Ⅰ，采用3个曲线形尖塔+粗糙元方法，布置如图1所示;(2)流场Ⅱ，采用格栅+粗糙元方法，其中格栅形式及尺寸见图2，所安放位置距试验模型中心8.0 m，隔栅正下方的每个方格空隙内放置粗糙元一个，其后再放置5排粗糙元(靠试验模型一侧)，横纵向间距均为50cm，前后排之间错开布置;(3)流场Ⅲ，采用尖塔+粗糙元+挡板方法，如图3所示.

图1 流场Ⅰ的尖塔立面图和模拟元件布置示意图(单位:mm)Fig.1 Sketch of spire elevation and configuration of simulating element of flow fieldⅠ(Unit:mm)

图2 流场Ⅱ隔栅示意图(单位:mm)Fig.2 Sketch of the fence of flow fieldⅡ(Unit:mm)

以上3种流场采用的粗糙元尺寸均为8.0cm× 6.5cm×5.0 cm，其迎风面为8.0 cm×5.0 cm.文献［10］中给出了这3种地貌模拟的详细介绍，表1中列出了这3种流场的地貌特征及风场参数，同时列出了TTU实测及其它研究机构进行TTU标模试验的相应参数.由表1可见:流场Ⅱ、Ⅲ的湍流度显著高于流场Ⅰ且较接近于实测情况，但包括本试验在内的所有积分尺度的模拟结果均明显比实测的小(且文中流场Ⅱ的积分尺度最小)，积分尺度和实测结果的差异是影响风洞试验和实测结果差别的因素之一.此外在风场模拟试验中发现［10］:平均风速剖面对格栅的横向竖向间距、位置特别敏感;流场Ⅲ的脉动风速谱、湍流度和积分尺度在总体上均优于其它两种流场，由此可初步判定流场Ⅲ是较为理想的选择.

图3 流场Ⅲ的尖塔立面图和模拟元件布置示意图(单位:mm)Fig.3 Sketch of spire elevation and configuration of simulating element of of flow fieldⅢ(Unit:mm)

表1 由不同研究单位和大学模拟得到的风场参数比较1)Table 1 Comparison of simulated wind field parameters by different research institutes and universities

1.2 TTU试验模型及试验数据处理

试验中分别按几何缩尺比1∶15、1∶30、1∶45制作了3个TTU模型，依据TTU实地模型的测点位置［3］，从中选取了40个测点布置在每个风洞试验模型表面，测点位置及编号(为便于数据分析比较，对所选取的40个测点在原有测点编号基础上，又按1～40的顺序重新定义了编号，并标注在原测点编号之后的括号内)见图4，实地模型尺寸及风向角定义方式见图5.所有测点除1∶45模型表面的测点14、17及20(即对应原型的43807、44207及44407号测点)位置与要求不符外，其它测点位置均准确无误且测压软管管路通畅.

图4 TTU模型测点位置Fig.4 Tap locations of TTU model

图5 TTU建筑实际尺寸、风向角及典型测点位置Fig.5 Dimensions of the full-scale TTU model，azimuth and typical tap locations

试验得到的平均风压系数和脉动风压系数均以各缩尺模型顶部高度处(即原型4m高度)的风压作为无量纲化的参考风压.平均风压系数、峰值风压系数和均方根风压系数可表示如下:

式中，¯p为采样周期T内得到的平均风压，p0为参考静压，ρ为空气质量密度，vH为模型屋面高度H处的平均风速，^p为仿照实测直接从测量得到的风压时程序列挑选极值得到的峰值负压，˜p为脉动风压均方根值.

2 试验结果与分析

2.1 模型缩尺比的影响

首先在流场Ⅰ中分别进行了1∶15、1∶30、1∶45 3种缩尺模型的试验，它们对应的最大堵塞度分别为4.9%、1.2%和0.6%.通过同种流场下不同缩尺比模型间风压系数的对比，分析模型缩尺比对风洞试验结果的影响.

图6、图7分别给出了来流垂直(风向角为90°和180°)吹向模型墙面和倾斜(风向角220°和230°)吹向墙面时，以1∶30模型结果为基准，与其它两个模型的平均、脉动风压均方根系数的对比结果.

图6 不同缩尺比模型平均风压系数比较(流场Ⅰ)Fig.6 Comparison of mean wind pressure coefficients of different scale models in flow fieldⅠ

图7 不同缩尺比模型均方根风压系数比较(流场Ⅰ)Fig.7 Comparison of RMS wind pressure coefficients of different scale models in flow fieldⅠ

由图6、7可见，所有数据基本上落在斜率为1的直线附近，这意味着由不同缩尺比模型得到的数据总体上是一致的.但进一步观察不难发现:1∶30与1∶45模型间试验数据的吻合程度明显高于1∶30与1∶15模型，脉动风压系数的一致性也高于相应的平均风压系数.进一步对以10°为间隔的36个风向角下所有测点数据进行回归分析，结果显示: 1∶30与1∶15模型间平均风压系数平均率的回归线斜率在0.93～1.07之间，而1∶30与1∶45模型间该斜率在0.96～1.04内;对于脉动风压系数，1∶30与1∶15、1∶45模型间风压系数平均率的回归线斜率分别位于0.95～1.05和0.99～1.01之间.这显示1∶30模型和1∶45模型的试验结果更接近，且模型大小对平均风压的影响要比对脉动风压显著.

产生上述现象的原因是多方面的，如模型的风洞堵塞度、雷诺数、模型对应于同一原型高度上的湍流度、湍流积分尺度的变化等，但就风压较高区域上平均风压相差相对较大(尤其是负压)而脉动风压相对接近这一现象，可以认为模型风洞堵塞度是造成平均风压差异的主要因素，这可由试验时毕托管测得的静压，即式(1)中的参考静压p0随风向角的变化进一步说明，结果见图8.

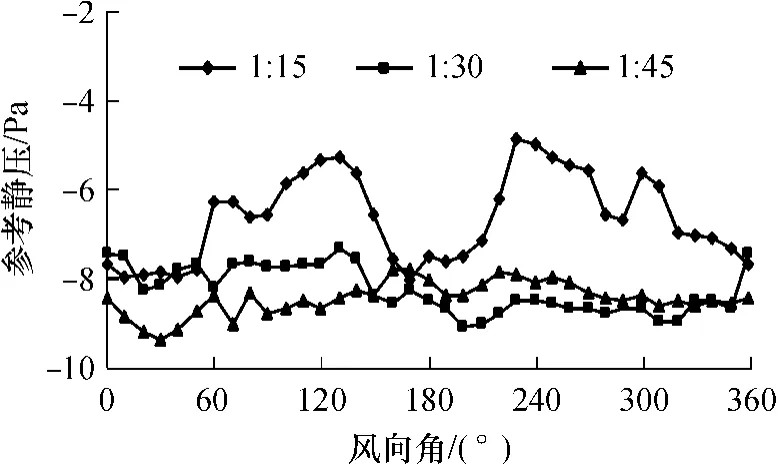
图8 毕托管静压随风向角的变化(流场Ⅰ)Fig.8 Static pressure of the Pitot tube versus azimuth in flow fieldⅠ

由图8可见:风洞试验中由毕托管测得的静压也是随风向角的变化而变化的，小波动情况一般是源于试验的随机误差，但图中显示缩尺比为1∶15的模型的静压随风向角的波动幅度明显大于其它两种缩尺比情况，且其最小静压值通常出现在模型迎风面积较小时(0°和180°)，最大静压则出现在模型迎风面积较大时.迎风面积较大意味着模型的堵塞度较大，而堵塞度较大会影响风压系数测量的准确性，图6(a)所示的偏离程度最大的230°风向角和图8所示的最大堵塞度所在的风向角相吻合.这些特征明显和模型对流场的堵塞影响直接相关.

应该指出的是，1∶15缩尺比模型所对应的堵塞度为4.9%，这在风工程中仍然是可以接受的，但为了减小模型缩尺比变化对风洞试验结果的影响，后续低矮建筑的风洞试验宜采用堵塞度相对较小的模型进行.

2.2 3种流场试验结果的对比

2.2.1 模型中心横断面测点的风压分布

将缩尺比为1∶30的模型在3种不同流场中进行试验，以鉴别不同流场模拟方式的效果，寻求更为合理的流场模拟方法，从而为后续低矮建筑的风洞试验提供更符合实际的流场.

图9－11分别绘出了60°和90°风向角下，模型屋面和墙体横向中轴线(ABCD，参见图5)上11个测点在不同流场中风压系数的对比.图中流场Ⅱ和流场Ⅲ给出的是风压系数的变化范围(多次重复性采样的结果)，均用彩色粗实线表示，为加以区分，特将流场Ⅱ对应的测点风压系数变化范围绘制在稍稍偏离测点的位置上.图中还给出了西安大略大学1∶100模型上5个测点的风压系数值［12］及同济大学TJ-2风洞1∶50模型的试验结果［11］.

对于平均风压系数，图9所显示的流场Ⅰ的结果基本都落在了实测结果的范围之内，且负压时其结果总是略高于其它两种流场;屋面上，流场Ⅱ、Ⅲ的平均风压系数值相差不大，与实测结果和其它风洞的试验结果较为接近;墙面上，流场Ⅱ的试验结果基本落在了实测范围之内，而流场Ⅲ的结果明显高于(正压时)或低于(负压时)实测结果，其与流场Ⅰ试验结果的差别都在20%以上;流场Ⅲ中试验值的变化范围大于流场Ⅱ的结果.

图10的脉动风压系数分布显示:随着流场湍流度的升高，脉动风压系数也在不断增大，湍流度相对较大的流场其脉动风压系数也较大;90°风向角下，流场Ⅲ中的试验结果全部落在实测值范围之内，但在60°风向角下，尽管较流场Ⅰ、Ⅱ其结果更接近实测值，但还是存在较明显的差异;单就脉动风压而言，流场Ⅱ、Ⅲ的结果更接近于实测结果.

峰值风压系数(见图11)是直接从试验样本中挑选的极值，其随机性较强，变化范围也较大，随着流场湍流度的升高，峰值风压系数的变化范围也会相应增大(尤其是在屋面上);60°和90°风向角下，流场Ⅱ、Ⅲ的结果与实测值保持了较高的吻合度，特别是流场Ⅲ中获得的试验结果更为令人满意.

图9 典型风向角下平均风压系数的分布Fig.9 Distribution of mean wind pressure coefficients at typical azimuths

图10 典型风向角下均方根风压系数的分布Fig.10 Distribution of RMS wind pressure coefficients at typical azimuths

从上述结果可以看出:流场Ⅰ的湍流度尽管不高，但在平均风压和实测值方面还是较为吻合的;流场Ⅱ和流场Ⅲ中平均、脉动和峰值风压的模拟结果与实测值的吻合程度依次升高，特别是峰值结果，其变化范围基本都在实测范围以内，脉动风压与其它研究机构的结果较为接近，但与实测值还存在一定差距;模型屋面高度上的湍流度由流场Ⅰ的13%升高到流场Ⅱ、Ⅲ的20%左右，湍流度升高后相应的脉动风压值会增大，且与实测结果的差距有所减小，但从采用了与实测风场一致的湍流度指标来看，湍流度并不是决定风压脉动值高低的唯一因素.

图11 典型风向角峰值下风压系数的分布Fig.11 Distribution of peak wind pressure coefficients at typical azimuths

2.2.2 屋面典型测点的风压分布

以下进一步对比在流场Ⅱ、Ⅲ两个风场下屋面典型测点的风压系数随风向角的变化情况，限于篇幅仅分析平均和峰值负压系数的变化情况.

(1)模型屋角测点50101

低矮房屋的屋角是气流变化最为剧烈的位置，在正对屋角的斜风作用下，受锥形涡的影响其风压值往往是屋面所有区域上最高的，实际建筑屋面的破坏通常都源于此，因此，屋角测点风压的准确模拟是评价风洞试验模拟效果的重点.图12给出了屋面角区50101测点的风压系数随风向角的变化.

由图12中可见，对于平均风压系数，文中结果和原型实测数据以及TJ-2风洞的结果吻合较好;而对于关键的峰值负压系数，文中结果要比TJ-2风洞的试验结果更接近实测数据，但在风压较高的180°～250°范围内与实测结果依旧存在差别，同时注意到流场Ⅲ的结果优于流场Ⅱ的结果.

(2)模型屋面边缘测点50209

测点50209位于模型长边方向上，图13显示了与50101较为相似的风压变化特征.平均风压系数与实测结果基本一致;峰值负压系数的峰值出现在来流正对屋角的225°风向角附近，此时风洞试验结果与实测结果的差别依然存在，在整体上，文中结果要好于TJ-2，且流场Ⅲ的结果优于流场Ⅱ的结果.

图12 屋顶角区50101测点风压系数Fig.12 Wind pressure coefficients of tap 50101 at the corner region

图13 屋面边沿附近50209测点风压系数Fig.13 Wind pressure coefficients of tap 50209 near roof edge

(3)屋面内部测点50909

50909测点位于屋面内部，该点处位置已经脱离流体剧烈变化的区域，风洞试验基本可以反映其真实的风压特性，平均风压系数的试验结果与实测本重叠，峰值负压风压系数也基本处在实测范围之内，但流场Ⅲ的结果优于流场Ⅱ，如图14所示.

图14 屋面内部区域50909测点风压系数Fig.14 Wind pressure coefficients of tap 50909 in the interior region

3 结论

(1)试验时对毕托管的静压变化的监测显示1∶15缩尺比模型的堵塞效应仍较为明显，4.9%堵塞度的影响依然存在，并会影响到结果的准确性.风洞试验中应合理地选择模型缩尺比，建议采用较小尺度的模型进行试验.

(2)和流场Ⅰ相比，流场Ⅱ、Ⅲ的流场湍流度和实测值更接近，因而其模型的试验结果与实测值较为一致.对于位于高湍流区的低矮房屋，建议采用湍流度高的流场进行试验.

(3)格栅方式的横向、竖向间距和位置对风场参数较为敏感，且受限于其结构特征、模拟出的积分尺度也不太理想，综合文中和其它文献的研究结果和结论，建议采用流场Ⅲ作为低矮建筑的风洞试验流场.

［1］ Cao S Y，Ge Y J，Tamura Y.Wind damage in China caused by Typhoon Rananim［C］∥Proceedings of the Sixth Asia-Pacific Conference on Wind Engineering.Seoul:Korea Society for Wind Engineering，2005:200-209.

［2］ Levitan M L，Mehta K C.Field measurements of pressures on Texas Tech Building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1991，38(2/3):227-234.

［3］ Levitan M L，Mehta K C.Texas Tech field experiments for wind loads(Part 1):building and pressure measuring system［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，43(1/2/3):1565-1576

［4］ Levitan M L，Mehta K C.Texas Tech field experiments for wind loads(Part 2):meteorological instrumentation and terrain［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，43(1/2/3):1577-1588.

［5］ Sharma R N，Richards P J.Net pressures on the roof of a low-rise building with wall openings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93(4): 267-291.

［6］ Mehta K C，Levitan M C，Iverson R E，et al.Roof corner pressure measured in the field on a low building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41(1/2/3):181-192.

［7］ Lin J X，Surry D，Tieleman H W.The distribution of pressure near roof corners of flat roof low buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，56(2/3):235-265.

［8］ Hee J，Ham J，Bienkiewcz B.Wind tunnel simulation of TTU flow and building roof pressure［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，77/78: 119-133.

［9］ Tieleman H W.Model/full scale comparison of pressures on the roof of the TTU experimental building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1996，65(1/2/3):133-142.

［10］ 刘帅.TTU标模及平顶罩棚类低矮建筑的风洞试验研究［D］.汕头:汕头大学土木系，2006.

［11］ 罗攀.基于标准模型的风洞试验研究［D］.上海:同济大学桥梁与遂道工程专业，2004.

［12］ Surry D.Pressure measurements of Texas Tech Building: wind tunnel measurements and comparisons with full scale［J］.Journal of Wind Engineering and Industrial Aerodynamics，1991，38(2/3):235-247.