边坡应力重塑作用的模拟分析

阳 栋， 王国体， 许靖华， 吕志学

(1.合肥工业大学土木与水利工程学院，安徽合肥 230009;2.黑龙江省水土保持科学研究所，黑龙江哈尔滨 150400)

土体中一点的应力状态可以用摩尔圆来表示，如果把抗剪强度线τf=c+σtanφ与土体中某单元体的应力状态摩尔圆绘在同一个图上，就可以根据摩尔圆与抗剪强度线的关系，明确地判别土体单元是否处于极限状态。如图1所示，对于摩尔圆O1，剪应力τ=(σ1-σ3)/2＜c+σtanφ，单元体处于稳定状态。如果保持土的强度参数c、φ不变(即图1中强度直线不变)，单独减小最小主应力σ3(最大主应力σ1不变)，将导致摩尔圆半径增大，即最大剪应力τ增大，当τ增大到与直线相切时，边坡达到极限状态(图1中圆O2所示);如果σ1、σ3同时减小，则相当于把摩尔应力圆向左移，此时即便σ1比σ3减小更多，单元体依然很容易达到极限状态，如圆O3所示[1，2]。

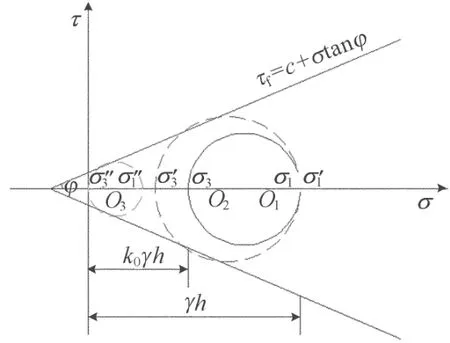
图1 单元体应力状态

边坡开挖将导致坡面土体应力释放。在开挖前，土体内部单元受自重力作用，其最大主应力为竖向重力σ1=γh，最小主应力方向为水平向，如图2a所示，大小为σ2=σ3=k0γh，k0为侧压力系数。在开挖后，原来作用在坡面上的重力及水平侧压力被卸除，边坡土体内部应力发生变化，坡面附近土体最大主应力方向约为平行坡面方向，而最小主应力方向为垂直坡面方向，大小接近0，如图2b所示。

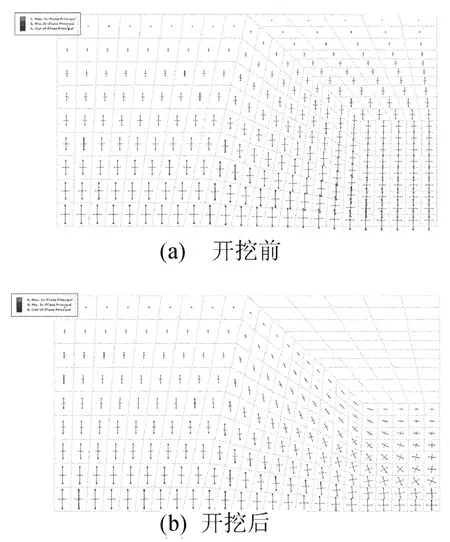
图2 边坡开挖前、后土体中大小主应力的分布

1 应力重塑法的基本内容及实现

1.1 应力重塑法的基本内容

由于具有半空间平面的任何土体，在自重应力的状态下必定是稳定的。设想由于工程的某种需求，需要开挖基坑或渠道的边坡，如果在开挖、卸去或除去土方的质量之后，再设法通过工程措施恢复该土方质量对于坡面处引起的应力，并使该应力等于未开挖之前的、原本稳定的应力状态，坡面就会象未被开挖之前一样，保持原来稳定的应力状态，这就是应力重塑的基本原理。

应力重塑思想认为，滑坡的治理与防治，最重要的是抓住其内因，并结合考虑外因。这个内因就是坡体及临坡面在开挖卸荷后的零应力状态及其相应的土体强度变化，而土体的强度又受土体的历史应力状态所影响，因此，坡面土体的应力状态控制显得极为重要。采用特定的措施及手段，重塑原有土体的应力状态，使得挖坡后和挖坡前的土体应力基本一致，这样，挖坡后的土体就会一直保持原本天然土体的稳定状态，这就是应力重塑方法。同时，采用重塑应力的措施又使其有利于增加坡面土体的抗剪能力[3-5]。

1.2 应力重塑方法的实现

应力重塑方法在工程中已有一些应用，如在基坑支护中采用对支撑，可以有效防治土体变形，维持坑壁稳定。而对于坡面工程，可以考虑设计框架梁结合各种形式的扩体型预应力锚杆，在坡面上施加预应力，使得锚杆产生的预紧力转移到坡面土体表面时，土体的应力状态能够达到或超过开挖前的情形，坡面土体呈现固结压缩状态，随着固结的发展和完成，将进一步提高坡面附近土体的抗剪能力。

2 开挖边坡应力重塑的有限元模拟

2.1 模型简介

一开挖边坡，坡高20 m，坡度45°，坡顶到右端边界的距离为50 m，坡脚到左端边界的距离为30 m，坡脚到底边界取20 m。土的参数γ= 20 kN/m3，黏聚力c=42 kPa，内摩擦角φ=17°，剪胀角ψ=0°，弹性模量E=100 MPa，泊松比ν= 0.3，边坡底面采用水平和竖直位移约束，左右边界水平位移约束，采用理想的弹塑性模型和Mohr-Coulomb屈服准则。

2.2 模拟步骤

(1)地应力平衡步。先施加重力，然后导出在重力场作用下各单元质心的应力值，并将其作为初始应力场施加在模型上，与重力相平衡，从而消除重力对变形的影响。

(2)模拟开挖过程。通过编辑关键字，用语句*MODEL CHANGE，TYPE=ELEMENT，REMOVE Set-1命令实现边坡的开挖。

(3)在坡面上施加重塑应力。在ABAQUS中，开挖形成的表面用内表面方式选取，表面不均匀分布力通过编制子程序或用分析场函数加载。

(4)对土体强度参数进行折减，直至边坡达极限状态[6-10]。

2.3 结果分析

(1)当边坡开挖结束后，如果不进行应力重塑，直接进行强度折减，在t=2.200 8 s处(如图3a所示)，当折减系数为1.221时，351点位移突变，图4a、图5a所示分别为此时的等效塑性应变图和位移图(极限状态以特征点位移突变为标准)。在折减系数为1.230时，等效塑性区贯通。而此边坡在Geoslope中采用M orgensten-Price极限平衡法计算得到的安全系数为1.20，故用2种不同极限状态判别标准的强度折减法计算的安全系数相对于极限平衡法的误差分别为1.7%和2.5%。

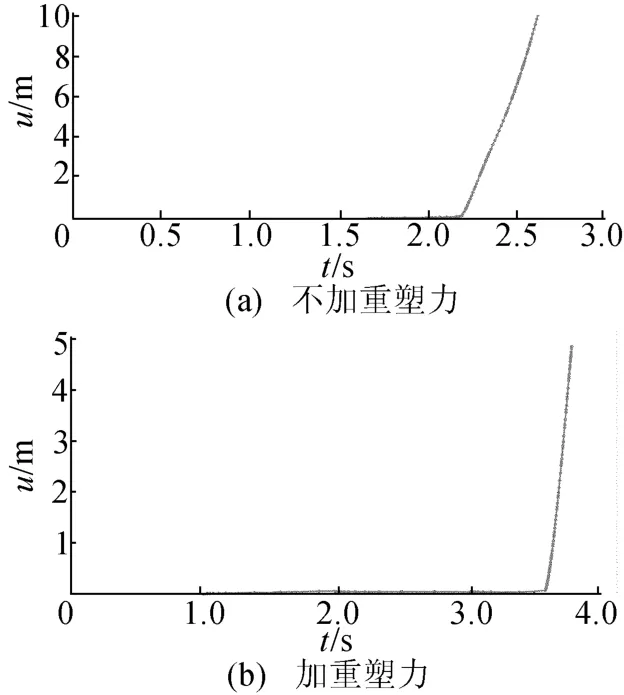
图3 351节点位移随时间变化曲线

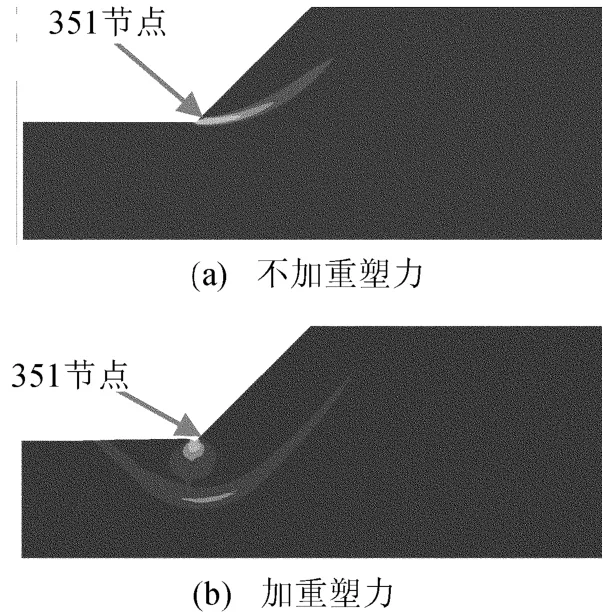
图4 极限状态下的等效塑性应变图

(2)当在坡面上施加垂直于坡面，大小为P=0.7γh的重塑应力时，在t=3.585 9 s处，351点位移发生突变，如图3b所示，此时计算得重塑后的安全系数为2.116，相比应力重塑前提高73.3%。由此可见，采用应力重塑方法加固边坡，提高安全系数的效果显著。对比重塑前、后边坡极限状态时的等效塑性应变图(图4a、4b)和位移图(图5a、5b)可知，在进行强度折减达极限状态时，滑动面发生了变化，滑面加深了，同时滑体的体积增大许多，而且位移和等效塑性应变的最大值由坡面下部转变到坡脚前缘处。

2.4 边坡土体应力分析

为分析重塑前、后坡体内应力变化规律，在坡体内选取初始潜滑面ABC(本文称开挖后直接进行强度折减形成的滑面为潜滑面)和水平路径DE，如图6和图7所示，对比选定路径上土体在应力重塑前后的应力变化情况。

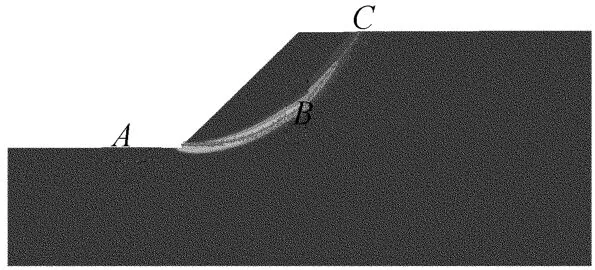
图6 滑面ABC

图7 水平路径DE

图8所示中，曲线1代表初始状态(开挖前)潜在滑面ABC上土体节点的最小主应力;曲线2代表开挖后潜在滑面ABC上土体节点的最小主应力状态;曲线3代表应力重塑后潜在滑面ABC上土体节点的最小主应力状态;曲线1′、2′、3′分别代表相应状态的最大主应力(在ABAQUS中拉应力为正，压应力为负，而在土力学计算及莫尔圆的绘制中，都以压应力为正，拉应力为负)。

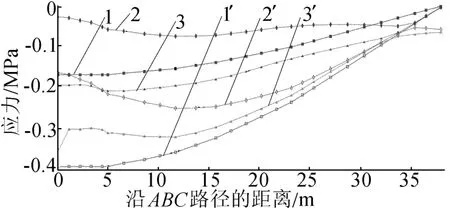
图8 滑面ABC上不同步的大小主应力图

由图8可以看出，边坡开挖后，潜在滑面上节点的大小主应力绝对值都减小，而大小主应力差变化不大，即相当于潜在滑面ABC上每个节点的摩尔应力圆从右往左移，同时摩尔圆半径和强度曲线不变，节点单元从安全状态变到逐渐接近极限状态，当施加垂直坡面大小为0.7γh的力，进行应力重塑后，大小主应力重新增大到接近初始状态的位置，边坡恢复到稳定状态。

图9所示中，曲线4代表水平路径DE上节点的初始状态(开挖前)水平力;曲线5代表开挖后的水平力，曲线6代表应力重塑后的水平力。

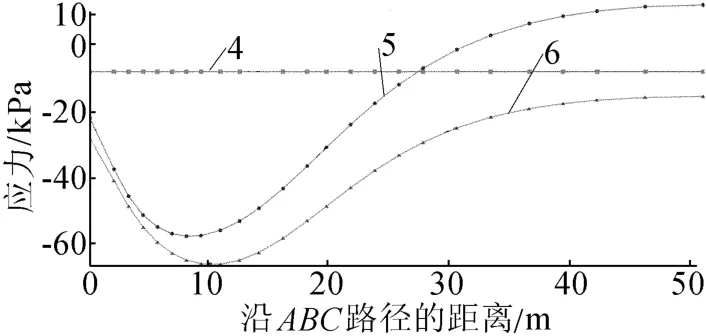
图9 水平路径DE上节点的水平力

由图9可知，在开挖前土体处于自重应力状态下，水平方向力为压力，在ABAQUS中为负值，而开挖后，开挖面附近的水平压应力增大，在离开挖面较远的地方，水平力出现正值，即出现拉应力，而土体基本上是不能承受拉应力的，故开挖后坡后土体表面将出现拉裂缝。由曲线4、6的对比可知，在进行应力重塑后，土体单元的压应力相比初始压力增大许多，拉应力完全消失，故重塑后的土体中不可能出现拉裂缝，有利于边坡的稳定。

3 不同加载方式下应力重塑效果

边坡在不同大小和方向的重塑应力作用下，坡体稳定状况不同，本文将分析重塑力方向和大小变化对边坡应力重塑效果的影响。

3.1 坡面施加不同方向重塑应力的对比分析

当坡面上施加不同方向的重塑应力时，重塑的效果不同。为了找出指定边坡(2.1节)最佳的重塑力加载方向，以5°为间隔，对不同方向重塑应力作用下的边坡进行模拟，计算其安全系数，结果见表1所列(重塑力大小为0.7γh)。

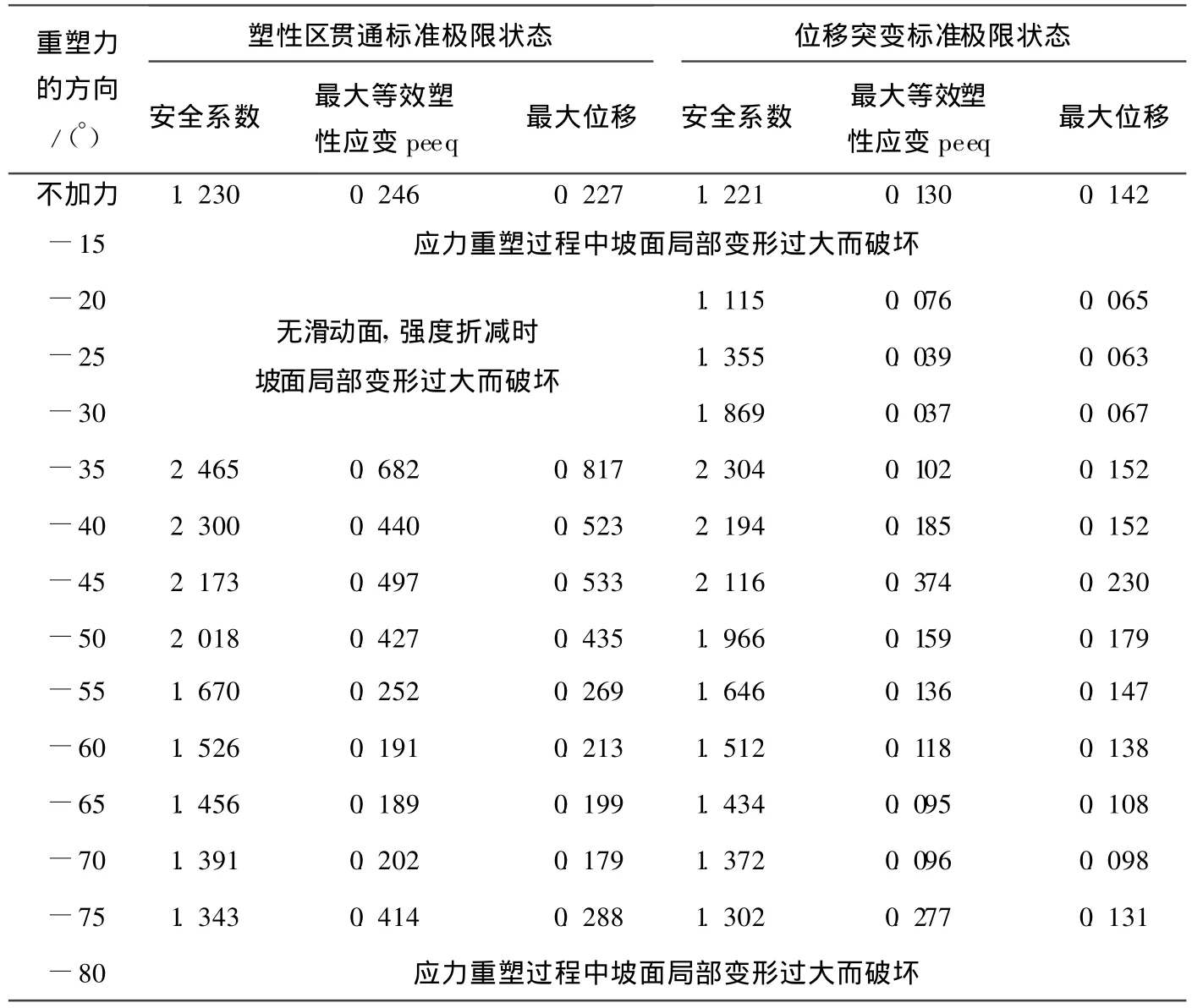
表1 施加不同方向重塑力时安全系数变化情况

由表1可知，对于本文45°坡，当重塑力大小为0.7γh时，无论是以特征点位移突变还是塑性区贯通作为极限状态的判断标准，当重塑力与水平方向呈-35°时，安全系数最大，重塑效果最好，最大等效塑性变形和位移都发生在坡脚附件的水平区域。

而当重塑力的方向与水平夹角小于30°或大于80°时，在强度折减过程中无滑动面的产生，坡面局部变形过大导致不收敛。

3.2 坡面施加不同大小重塑应力的对比分析

同样算例，以0.1γh为间隔，对坡面施加不同大小的重塑力，并进行强度折减，所得结果见表2所列(重塑力方向垂直坡面)。

由表2可知，对于本文45°坡加垂直坡面的重塑力，当重塑力≥0.8γh时，在强度折减过程中不出现滑动面，在坡面滑动之前地基先破坏，边坡的安全系数大于地基稳定系数，此时加过大的重塑应力是不经济的。

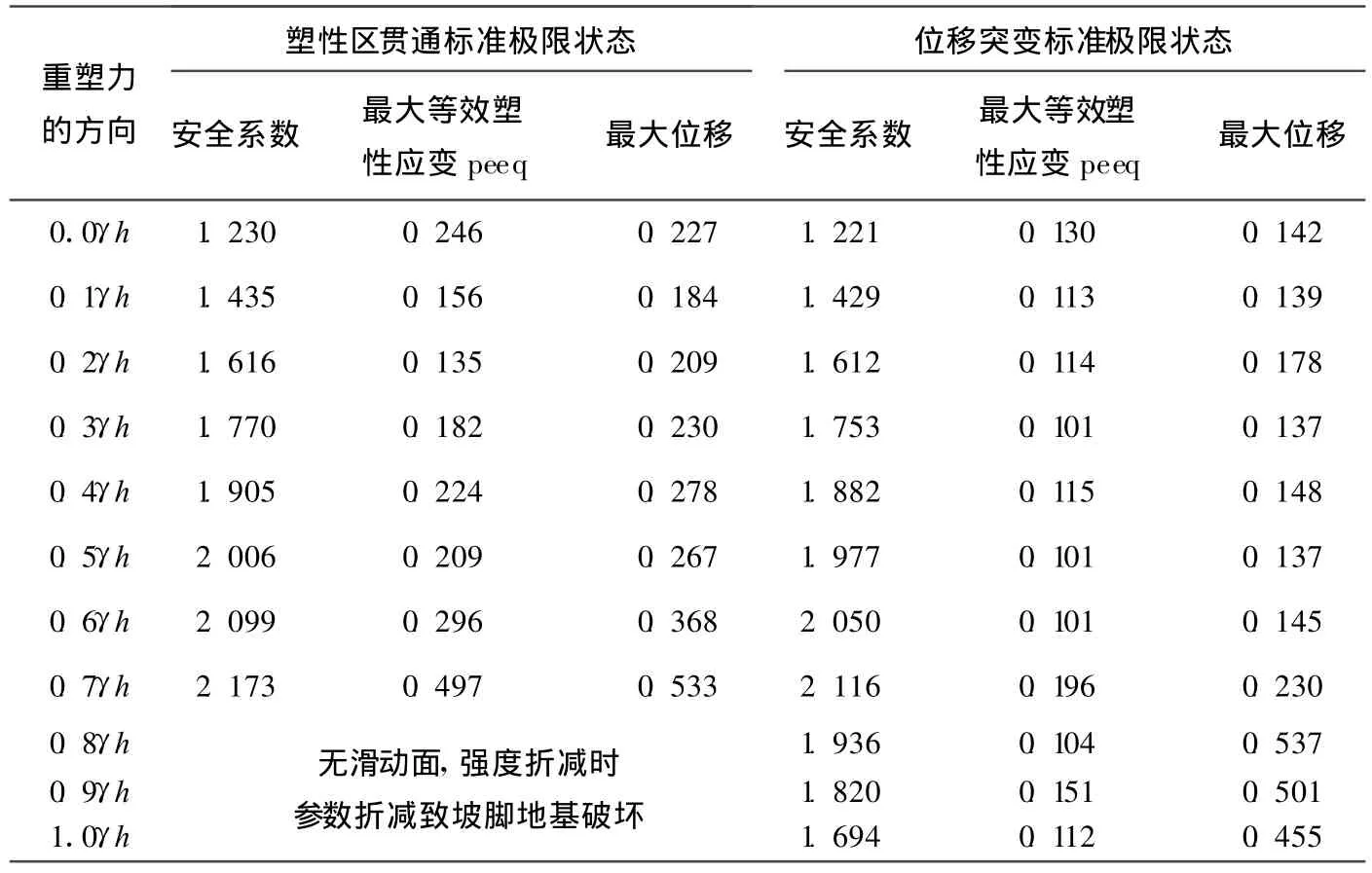
表2 施加不同大小重塑力时安全系数变化情况

4 结 论

(1)采用应力重塑的方法能够使边坡土体恢复到接近开挖前的应力状态，消除拉应力，显著增大边坡的安全系数，增强边坡的稳定性。对于本文算例边坡，当施加与水平方向成-35°，大小等于0.7γh的重塑力时，安全系数最大能从1.221提高到2.304。

(2)当重塑力较大时，在强度折减过程中，与坡面法向夹角较大的加载，将产生坡面局部剪切破坏，而不形成滑动面。基于典型边坡的分析，最佳加载方向并不是在垂直于坡面的方向，而是在垂直方向的基础上向水平方向旋转一定角度，本文单一算例的最佳加载方向为-35°。

(3)用有限元强度折减法计算分析时，对于确定参数的边坡，重塑应力具有最佳值。重塑力过大将导致强度折减过程中坡下地基失稳。本文算例中，加0.7γh重塑力时能获得最大的安全系数。

[1] 陈忠汉，黄书秩，程丽萍.深基坑工程[M].北京:机械工业出版社，2002:14-16.

[2] 卢廷浩.土力学[M].南京:河海大学出版社，2002: 158-161.

[3] 王国体.应力重塑方法及其工程实现[J].岩土工程学报，2003，25(6):750-753.

[4] 王国体，易志宏，胡志专，等.开挖边坡中应力重塑方法的有限元模拟[J].合肥工业大学学报:自然科学版，2004，27 (4):368-371.

[5] 易志宏.应力重塑方法在开挖边坡治理中的应用研究[D].合肥:合肥工业大学土木与水利工程学院，2004.

[6] 曹先锋，徐千军.边坡稳定分析的温控参数折减有限元法[J].岩土工程学报，2006，28(11):2039-2042.

[7] 王金昌，陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社，2006:16-20.

[8] 朱以文，蔡元奇，徐 晗.ABAQUS与岩土工程分析[M].香港:中国图书出版社，2005:150-151.

[9] 滦茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报，2003，23(2): 1-8.

[10] 刘 华，钱德玲，付 聪.基于ABAQUS的软土地基加固有限元分析[J].合肥工业大学学报:自然科学版，2009，32 (8):1229-1232.