基于动态逆的高超声速飞行器鲁棒自适应控制

黄喜元 王 青

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

董朝阳

(北京航空航天大学 航空科学与工程学院，北京 100191)

基于动态逆的高超声速飞行器鲁棒自适应控制

黄喜元 王 青

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

董朝阳

(北京航空航天大学 航空科学与工程学院，北京 100191)

针对高超声速飞行器运动学模型具有高度非线性、多变量耦合及参数不确定等特点，提出了一种基于非线性动态逆的控制系统鲁棒自适应控制器设计方法.该方法将飞行器的运动方程分成速度子系统和高度子系统，利用控制输入的功能分配，并结合虚拟控制指令设计与非线性动态逆技术，实现速度和高度的稳定跟踪.为消除系统中模型不确定性和外界干扰的影响，采用鲁棒自适应滑模控制策略进行补偿.仿真结果表明:所提出的控制器设计方法不仅满足飞行器速度与高度跟踪性能的要求，且对模型不确定性和外干扰具有一定的鲁棒性.

高超声速;非线性动态逆控制;鲁棒自适应控制;滑模控制

高超声速飞行器由于自身复杂动力学特性的影响及其复杂的飞行条件，使得其动力学模型具有高度的非线性、强耦合及不确定性，因此，为高超声速飞行器设计控制系统是一项极富挑战的任务［1－2］.目前，针对具有非线性与参数不确定性的高超声速飞行器模型，国内外文献主要采用滑模控制［3］、鲁棒控制［4］和反演控制［5］的设计方法，基于输入输出线性化设计控制器，因此往往需要系统的精确模型，且得到的线性化模型复杂，不易于系统鲁棒性的分析.此外，这些文献的动力学模型简单，忽略了一些对控制系统设计有影响的耦合因素，如升降舵对升力的耦合，以及由冲压发动机位置而引起的推力与俯仰力矩的耦合等.

利用曲线拟合近似飞行器所受气动力和推力的方法，文献［6］提出了面向控制器设计的高超声速飞行器简化模型，该模型降低了高超声速飞行器非线性模型本身的复杂性，但保留了飞行器非线性模型的主要特性.本文基于此模型，采用非线性动态逆方法分别针对高超声速飞行器的速度子系统和高度子系统设计非线性控制器，并利用鲁棒自适应滑模控制技术消除系统中的模型不确定性和外界干扰的影响，既保证了飞行器速度与高度跟踪的性能，也提高了控制系统的鲁棒性.

1 高超声速飞行器模型描述

根据Lagrange方程，高超声速飞行器的纵向动力学模型可以描述为式中，V，h，γ，α，q 分别为飞行器的速度、高度、航迹倾角、攻角和俯仰角速度;m，Iyy，g分别为飞行器的质量、俯仰转动惯量和重力加速度;T，D，L，M分别为飞行推力、阻力、升力和俯仰转动力矩，且可利用曲线拟合近似描述成如下的形式:

为便于分析，令 x=［V，γ，α，q］T，式(1)写为

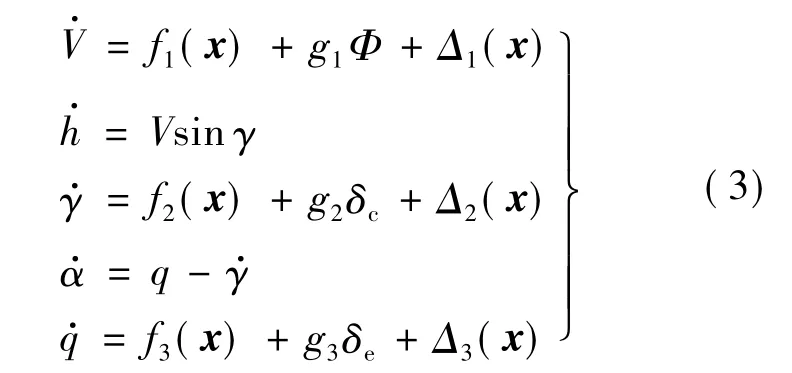
2 非线性控制器设计

高超声速飞行器控制器设计的目标是使得飞行器的速度和高度沿某参考轨迹到达期望的速度和高度，假定飞行器从初始速度和高度到达期望的速度和高度的参考轨迹分别为Vd和hd，因此，控制器设计的目标是调节跟踪误差V－Vd和hhd使其渐近收敛于0.

为实现上面的控制目标，将高超声速飞行器的运动方程分成两个子系统，分别为速度子系统和高度子系统，速度子系统仅采用Φ进行控制，高度子系统则采用δc和δe同时进行控制.在高度子系统控制器的设计过程中，为设计的方便，引入3个虚拟控制指令 γc，αc和 qc:γc用于直接控制飞行器的高度的变化，αc则被设计为高度子系统内回路的输入指令，qc用于实现α的控制，通过设计操纵舵偏δc和δe的控制律实现整个高度子系统的稳定.其控制框图如图1所示.

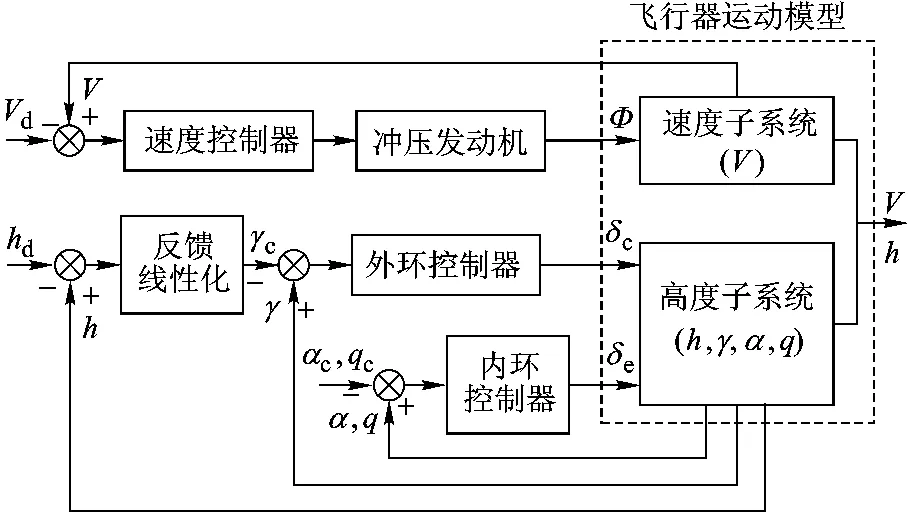
图1 高超声速飞行器的控制

2.1 速度子系统控制器的设计

定义跟踪误差为

为实现速度子系统的鲁棒控制，采用变结构控制策略，在状态空间寻找一个合适的滑动模态超平面，使得V跟踪Vd，定义滑模面为

当速度子系统滑动到该超平面时，从而得到一个渐近稳定的状态V→Vd，实现了控制目标.

对式(5)进行求导可得

设计控制律为

式中，k1＞0为控制增益设计常数.

由于高超声速飞行器飞行环境复杂，不确定项的界难以准确获得.为避免选择的太大而引起系统的振荡，采用自适应的方法对系统模型不确定性和外界干扰进行估计，则式(7)的控制律可修改为

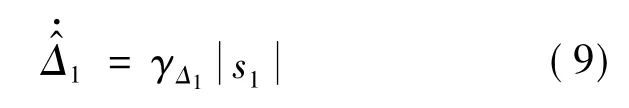
将式(8)代入式(6)得

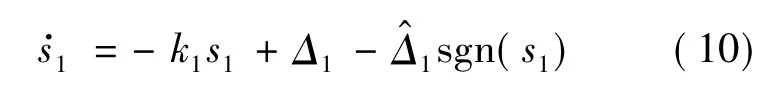
2.2 高度子系统控制器的设计

对于高度子系统，控制器设计的目标是使状态跟踪期望的控制信号，因此，可定义跟踪误差为

由于飞行航迹角可容许的变化范围很小，利用小角度函数的近似关系式sinγ≈γ，有

采用反馈线性化的方法，选择虚拟控制量为

式中，k2＞0为控制增益设计常数.式(12)可写为

考虑γ的控制，设计控制器δc，实现航迹角跟踪误差e3→0.定义滑模面为

对s2进行求导可得

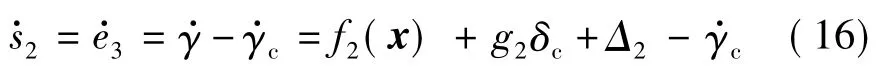
则δc的控制律可设计为

式中，k3＞0为控制增益设计常数.

式(16)的误差方程可以写为

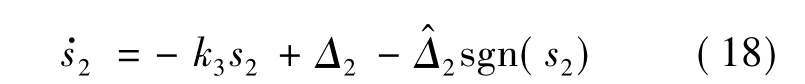
考虑α和q的控制，与h和γ的控制方法相似.首先设计虚拟线性控制器qc，将α的误差方程e4转化为稳定的形式，然后采用动态逆的方法设计δe的控制律，实现q的控制.

为实现上面的目标，取

式中，k4＞0为控制增益设计常数.则有

同样定义滑模面为

对其求导可得

利用动态逆的设计方法并考虑误差方程e4的交联影响，设计升降舵控制律为

式中，k5＞0为俯仰角速率的控制增益.同样将式(24)代入式(23)得

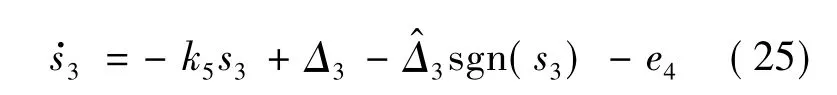
2.3 稳定性分析

选取准Lyapunov函数为

沿着系统式(10)、式(14)、式(18)、式(21)和式(25)的轨迹，对V进行求导可得

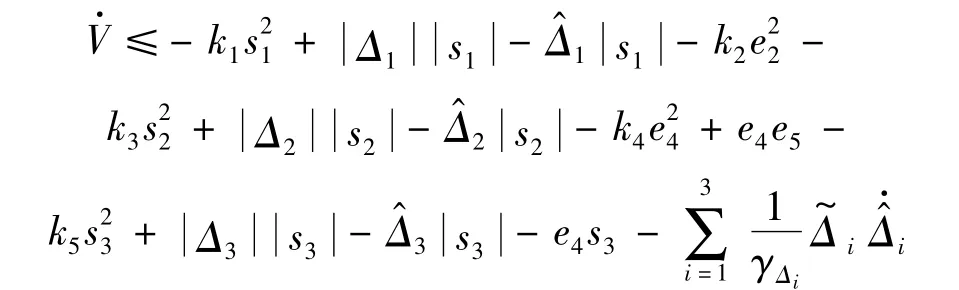
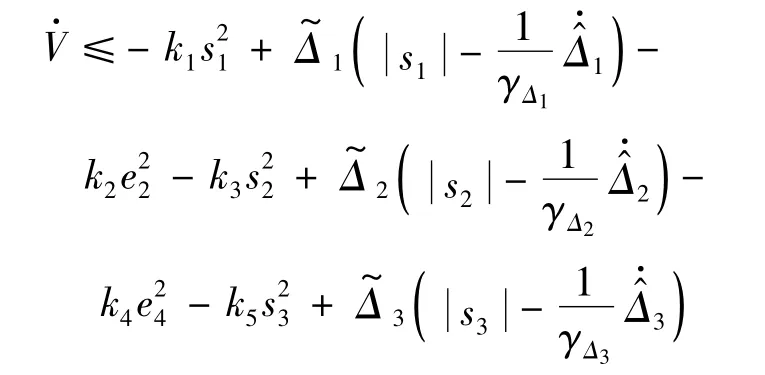
由自适应律式(9)、式(26)和式(27)，则有

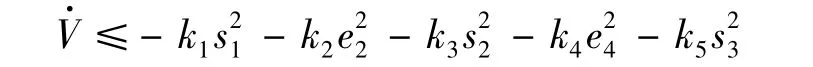
因此，闭环系统渐近稳定，系统内所有的信号在指定范围内有界.

由于在实际的应用中，控制律式(8)、式(17)和式(24)中的符号函数会产生抖振，为避免这一问题，采用饱和函数sat(si/ci)(i=1，2，3)代替符号函数sgn(si)，这里ci为边界层厚度.理论上，滑动变量si在有限的时间内不会精确地等于0，因此根据自适应律的形式，不确定项的估计值Δ^将会一直增大直到si=0，为克服这一问题，同时为避免控制量陷入饱和，采用死区和饱和限制技术修改式(9)、式(26)和式(27)中的自适应律为

式中，εi＞0 为小常数;为事先给定的常数，表示自适应参数的上界，且满足

3 仿真验证

仿真模型采用式(1)的非线性模型，仿真参数见文献［6］.初始值为 V0=2 347.6m/s，h0=25908m，γ0=0°，α0=2.8°，q0=0(°)/s.给定飞行器爬升100m的高度指令和提高30m/s速度指令，hd和Vd利用阶跃指令滤波得到.

仿真初始加入 Δ1=1m/s2，Δ2=10－3rad/s，Δ3=10－2rad/s2的常值干扰.控制器的参数设计如下:k1=5，k2=2，k3=5，k4=10，k5=20，γΔ1=1，γΔ2=0.5，γΔ3=1，仿真结果如图2 ～ 图 4 所示.

图2 高度及速度跟踪

图3 飞行航迹角与攻角

图4 控制输入

从图2～图4可以看出，基于非线性动态逆的鲁棒自适应控制器表现出了良好的控制性能.飞行速度和高度均很好地跟踪了各自的参考曲线，且具有较高的跟踪精度.γ，α也较好地跟踪了所设计的γc，αc，且控制输入均处于飞行器安全飞行的范围内.

4 结论

本文针对高超声速飞行器运动学模型具有高度非线性、多变量耦合及模型参数不确定等特点，提出了一种基于非线性动态逆的鲁棒自适应控制器设计方法.该方法采用非线性动态逆方法设计飞行器速度和高度跟踪的非线性控制器，并采用鲁棒自适应滑模控制策略提高了系统对模型不确定性和外界干扰的鲁棒性.仿真结果表明:所提出的控制器方法具有较好的跟踪性能与鲁棒性.

References)

［1］吴宏鑫，孟斌.高超声速飞行器控制研究综述［J］.力学进展，2009，39(6):756 －765 Wu Hongxin，Meng Bin.Review on the control of hypersonic flight vehicles［J］.Advances In Mechanics，2009，39(6):756 －765(in Chinese)

［2］ Fidan B，MirmiraniM，Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicle:review and new directions［C］//AIAA International Space Planes and Hypersonic Systems and Technologies.Norfolk，Virginia:AIAA，2003-7081

［3］ Xu H，Mirmirani M，Ioannou P.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control，and Dynamics，2004，27(5):829 －838

［4］ Wang Q，Stengel R F.Robust nonlinear control of a hypersonic aircraft［J］.Journal of Guidance，Control，and Dynamics，2000，23(4):577－585

［5］刘燕斌，陆宇平.基于反步法的高超音速飞机纵向逆飞行控制［J］.控制与决策，2007，22(3):313 －317 Liu Yanbin，Lu Yuping.Longitudinal inversion flight control based on backstepping for hypersonic vehicle［J］.Control and Decision，2007，22(3):313 －317(in Chinese)

［6］ Parker JT，Serrani A，Yurkovich S，et al.Control-orientedmodeling of an air-breathing hypersonic vehicle［J］.Journal of Guidance，Control，and Dynamics，2007，30(3):856 －869

(编 辑:刘登敏)

Robust adaptive control for hypersonic vehicle based on dynam ic inversion

Huang Xiyuan Wang Qing

(School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Dong Chaoyang

(School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

For the feature that hypersonic vehicle motion model is highly nonlinear，multivariable coupled and includes uncertain parameters，a robust adaptive control strategy based on nonlinear dynamic inversion for the hypersonic vehicle was proposed.By decomposing the vehicle motion equations into two subsystems，namely，a velocity subsystem and an altitude subsystem，and incorporating the design of virtual control commands and nonlinear dynamic inversion technology，the stable velocity and altitude tracking were achieved.To eliminate the effect of the model uncertainties and external disturbances，the robust adaptive sliding mode control method was adopted.Simulation results show that the proposed method not only satisfies the velocity and altitude tracking performance requirements，but also is robust to model uncertainties and external disturbances.

hypersonic;nonlinear dynamic inversion control;robust adaptive control;sliding mode control

V 271.9

A

1001-5965(2011)05-0560-04

2010-03-01

黄喜元(1983 －)，男，湖北新洲人，博士生，xy.huang999@gmail.com.