基于FDDPB方法的卫星姿态控制系统故障诊断
王新升 马 磊
(北京航空航天大学 宇航学院,北京100191)
梁 斌
(哈尔滨工业大学 空间智能系统研究所,哈尔滨 153001)
基于FDDPB方法的卫星姿态控制系统故障诊断
王新升 马 磊
(北京航空航天大学 宇航学院,北京100191)
梁 斌
(哈尔滨工业大学 空间智能系统研究所,哈尔滨 153001)
针对卫星姿态控制系统故障诊断问题,将执行机构及输出传感器的阶跃型和缓变型输出偏差统归于一种“参数偏差”型故障,介绍了改进的参数偏差型故障的实时检测与诊断 (FDDPB,Fault Detection and Diagnostics of Parameter Bias)算法,说明了此算法在卫星姿态控制系统执行机构和传感器故障诊断中的应用.引入卫星姿态动力学模型和飞轮模型,建立了算法仿真模型,选取执行机构阶跃型和缓变型故障作为故障注入条件,将该算法用于实验验证.仿真结果表明:该算法能够检测出系统发生的故障,且能够准确估计出故障幅值.
故障诊断;参数偏差;传感器;执行机构;故障模型
在轨运行的卫星承担着特定的空间探测、用户数据处理、先进技术验证等复杂的空间飞行任务.为了完成这些任务,要求其姿态控制系统具有高可靠性.但是由于空间环境恶劣,卫星受到内外干扰力矩的作用,卫星长期在轨工作无法避免姿控系统不发生故障.因此,及时有效地对卫星的姿态控制系统进行故障诊断,对保障卫星飞行任务的顺利完成是十分重要的.
文献[1]提出一种双观测器法,利用不同敏感器输出信号之间的解析冗余关系,对红外地球敏感器和陀螺进行了联合故障诊断;文献[2]采用自适应观测器诊断方法,对飞轮故障进行检测;文献[3]借鉴特征结构指定和故障检测滤波器的思想,提出一种滚动和偏航陀螺故障隔离的方法.上述方法都是针对特定的对象提出的,方法的移植性差,故障诊断开销大、效率低.
本文以强跟踪滤波器理论为基础,将执行机构及输出传感器出现的阶跃型或缓变型输出偏差统归于一种“参数偏差”型故障进行研究,并对执行机构发生的突变和缓变故障进行了仿真研究.
1 FDDPB算法及其应用
1.1 FDDPB 算法
考虑如下非线性系统:

式中,整数k≥0为离散时间变量;x∈Rn为状态变量;u∈Rp为输入向量;y∈Rm为输出向量;θ∈Rl为参数向量;非线性函数f(·),h(·)具有关于状态的一阶连续偏导数;Γ∈Rn×q为已知的矩阵;v(k),e(k)分别为q维和m维的0均值高斯白噪声,其协方差分别为Q和 R.假定 x(0)与v(k),e(k)统计独立.
执行机构及传感器阶跃型偏差故障描述为

执行机构及传感器缓变型偏差故障描述为

式中,Du(k),Dy(k)为k时刻的漂移量.
本文的任务是实时检测出式(1)系统是否发生了上述2类故障,若已经发生,则判别是哪类故障,并估计出故障的幅值.
为了完成上述任务,需要用到3种基础算法:非线性系统状态与参数的联合估计方法[4];阶跃型偏差的快速检测算法,其中故障检测采用残差加权平方和(WSSR,Weighted Sum of Squared Residuals)检测方法[5];修正的 Bayes 分类算法(MB,Modified Bayes Algorithm)[6].
参数偏差型故障的实时检测与诊断[7](FDDPB,Fault Detection and Diagnostics of Parameter Bias)的改进算法步骤如下:
1)由EKF(Extended Kalman Filter)及WSSR算法,在k=τ时判定式(1)系统是否发生了突变型参数偏差型故障,若是则转向3);否则继续本步监测,转向2).
2)由状态与参数的联合估计方法(滤波器采用STF(Strong Tracking Filter),渐消因子由近似算法计算)得参数估计值序列i=1,2,…,l;k=0,1,2,….基于 MB 算法判定k=τ时式(1)系统θi是否发生了缓变型偏差故障.若是,对i=1,2,…,l分别进行检验,得到发生此类故障的一组参数 θi,i∈{I1,I2,…,In1},故障幅值约为,转向1);否则转向3).
1.2 执行机构偏差型故障的检测与诊断
现采用如下模型对系统的执行机构偏差型故障进行检测与诊断:

令


则有

此时,基于式(5)可以采用FDDPB改进算法对此类故障进行检测与诊断.本文把u0(k)当成时变参数来处理.
1.3 传感器偏差型故障的检测与诊断
故障模型可取为

令

则式(6)可化成式(5)的形式,同样可采用FDDPB改进算法对此类故障进行检测与诊断.本文把y0(k+1)当成时变参数来处理.
2 卫星姿控系统模型建立
2.1 卫星姿态动力学模型
考虑由3个正交安装的反作用轮组与星体构成的动量系统,其姿态动力学方程为[8]

式中,I为卫星在本体坐标系中的转动惯量阵;ω =[ωx,ωy,ωz]T为卫星惯性角速度在本体坐标系中的分量;h为飞轮角动量;Td为干扰力矩,且

2.2 反作用飞轮数学模型
正常情况下,飞轮的数学模型[9]如下:

其中输入力矩为

式中,i=x,y,z;Tc=[Tcx,Tcy,Tcz]T为飞轮的输出控制力矩;Tf=[Tfx,Tfy,Tfz]T为飞轮摩擦力矩;h=[hx,hy,hz]T为飞轮角动量;J 为飞轮惯量阵;Ω =[Ωx,Ωy,Ωz]T为飞轮转速;hmax为动量轮最大角动量;Uh=[Uhx,Uhy,Uhz]T为输入控制指令,即控制器输出;Tmax为最大电磁输出力矩.

考虑飞轮摩擦力矩为

2.3 算法仿真模型
以上述卫星动力学模型和飞轮数学模型为基础,选取卫星惯性角速度和飞轮转速作为状态变量,可以构造出如下所示的非线性控制系统:

式中,u为执行器正常情况下的输出力矩Tc;d为干扰力矩
将式(11)系统进行Euler离散化,可以得到

3 计算机仿真分析
考虑执行机构偏差型故障,包括阶跃型偏差故障和缓变型偏差故障.根据第1节所述结论,故障模型为


则式(13)等价为

基于此系统,本文可以采用FDDPB改进算法进行故障的检测与诊断.

式中,H0,H1为系统无故障和有故障;TD为系统故障检测阈值,其值根据执行机构特性而定.
1)执行机构无偏差故障,即系统无故障.仿真结果如图1所示.
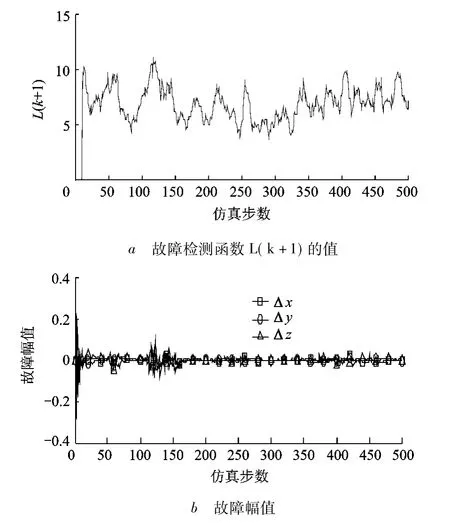
图1 执行机构无偏差故障的仿真图
由图1可以看出,在执行机构无偏差故障发生时,故障检测函数L(k+1)的值始终较小,故障幅值均趋于0.
2)执行机构阶跃型偏差故障.在仿真步数为200和400的时候分别注入阶跃型偏差故障u0x(k)=0.1,u0z(k)= -0.2.仿真曲线见图2.

图2 执行机构阶跃型偏差故障的仿真图
由图2可以看出,在仿真步数为200和400的时候,L(k+1)有较大幅度的上升,说明系统发生了阶跃型故障.由图2b可知在仿真步数为200的时候,Δx趋于0.1.在仿真步数400的时候,Δz趋于-0.2.由仿真曲线可知,故障幅值与注入的阶跃型故障大小保持一致.
3)执行机构缓变型偏差故障.在仿真步数在200~500的时候注入缓变型偏差故障u0y(k)=-0.002(k-200),在仿真步数在400~600的时候注入缓变型偏差故障 u0z(k)=0.001(k-400).仿真曲线如图3所示.
由图3可以看出,在注入缓变型故障之后,L(k+1)有了较平缓的上升,系统发生了缓变型参数偏差故障.由图3b可知故障幅值Δy,Δz与注入的缓变型偏差故障保持一致,跟踪效果良好.

图3 执行机构缓变型偏差故障的仿真图
4 结论
本文将卫星姿控系统易发生的几类突变和缓变故障统归为“参数偏差”型故障,介绍了“参数偏差”型故障检测与诊断改进算法.说明了该方法在姿控系统执行机构和传感器故障诊断中的应用,结合卫星姿态动力学模型和反作用飞轮数学模型,建立了算法仿真模型,并以执行机构突变和缓变故障为研究对象,将该算法用于计算机仿真实验中.实验结果表明,该算法能够准确检测出系统发生的故障,并且能够较快的准确估计出故障的幅值.
References)
[1]邢琰,吴洪鑫.一种红外地球敏感器和陀螺的故障隔离方法[J].计算机技术与自动化,2003,22(2):74 -76 Xing Yan,Wu Hongxin.A fault isolation method for infrared earth sensors and gyroscopes[J].Computing Technology and Automation,2003,22(2):74 -76(in Chinese)
[2]王小丽,倪茂林.基于自适应观测器的非线性系统故障诊断[J].空间控制技术与应用,2008,34(4):33 -37 Wang Xiaoli,Ni Maolin.An adaptive observer based fault diagnosis for nonlinear systems[J].Aerospace Control and Application,2008,34(4):33 -37(in Chinese)
[3]江耿丰,邢琰,王南华.利用特征结构指定隔离卫星滚动偏航陀螺故障的新方法[J].宇航学报,2007,28(3):557 -561 Jiang Gengfeng,Xing Yan,Wang Nanhua.A new fault isolation approach for the roll and yaw gyroscopes[J].Journal of Astronautics,2007,28(3):557 - 561(in Chinese)
[4]周东华,叶银钟.现代故障诊断与容错控制[M].北京:清华大学出版社,2000 Zhou Donghua,Ye Yinzhong.Modern fault diagnosis and fault tolerant control[M].Beijing:Tsinghua University Press,2000(in Chinese)
[5]周东华,席裕庚,张钟俊.一类非线性动态系统的故障检测策略与应用[C]//中国第四届空间及运动体控制技术学术会议.北京:[s.n.],1989:366 -374 Zhou Donghua,Xi Yugeng,Zhang Zhongjun.Fault detection approach and application for dynamic nonlinear systems[C]//The 4thChina Space Technology Conference.Beijing:[s.n.],1989:366-374(in Chinese)
[6]Zhou D H,Frank PM.Fault diagnostics and fault tolerant control[J].IEEE Trans on Aerospace and Electronics Systems,1998,34(2):420-427
[7]周东华,孙优贤,席裕庚,等.一类非线性系统参数偏差型故障的实时检测与诊断[J].自动化学报,1993,19(2):184-189 Zhou Donghua,Sun Youxian,Xi Yugeng,et al.Real-time fault detection and diagnostics based on nonlinear systems parameter bias model[J].Journal of Automation,1993,19(2):184 - 189(in Chinese)
[8]屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2001 Tu Shancheng.Satellite attitude dynamics and control[M].Beijing:Space Technology Press,2001(in Chinese)
[9]邢琰.卫星闭环姿态控制系统的故障检测与隔离[D].北京:中国空间技术研究院,2003 Xing Yan.Fault detection and isolation of satellite closed-loop attitude control system[D].Beijing:The Chinese Academy of Space Technology,2003(in Chinese)
(编 辑:文丽芳)
Fault diagnosis for satellite attitude control system based on FDDPB
Wang Xinsheng Ma Lei
(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Liang Bin
(Space Intelligence System Institute,Harbin Institute of Technology,Harbin 153001,China)
For satellite attitude control system fault diagnosis,step type and slow drift type output bias of actor and sensor were considered as parameter bias fault.Fault detection and diagnostics of parameter bias(FDDPB)algorithm and its application on actor and sensor of satellite attitude control system were introduced.The simulation models were proposed after describing satellite attitude dynamics model and wheel model.Simulations were finished on the assumption that step type fault and slow drift type fault occurred.Simulation results show that FDDPB algorithm could detect system fault and was able to estimate fault amplitude accurately.
fault diagnosis;parameter bias;sensor;actor;faultmodel
V 448.25
A
1001-5965(2011)05-0510-05
2010-03-08
国家863计划资助项目(2007AA704340;2007AA704115)
王新升(1973 -),男,黑龙江伊春人,讲师,xswang@buaa.edu.cn.

