三种虚拟阵元内插超分辨测向算法的性能对比
陈文晟 许小剑
(北京航空航天大学 电子信息工程学院,北京 100191)
三种虚拟阵元内插超分辨测向算法的性能对比
陈文晟 许小剑
(北京航空航天大学 电子信息工程学院,北京 100191)
对比研究了基于虚拟阵元内插的三种超分辨测向算法.在对多个小孔径雷达阵列的观测数据进行相干处理的基础上,分别应用非线性最小二乘迭代(NLS,Nonlinear Least Squares)、基于最小熵的反卷积迭代(IDMEC,Iterative Deconvolution algorithm based on Minimum Entropy Criterion)和最小加权范数(MWN,Minimum Weighted Norm)等算法构造雷达阵列间的各个虚拟阵元,合成大的孔径阵列以提高测向分辨率.通过仿真,验证了三种虚拟阵元内插算法的有效性,分析和比较了它们的超分辨性能和运算量.结果表明MWN法不仅具有最小的虚拟阵元构造误差和运算量,且有最好的测向性能.因此,总体上MWN法优于NLS法和IDMEC法.
虚拟阵元;超分辨;测向;内插
基于雷达阵列测向的常规波束形成算法,其角分辨力受到阵列物理孔径的限制(瑞利限)[1].所以,增大阵列孔径是提高测角分辨率的有效方法.但实用中增大天线物理孔径受到诸多因素制约,为克服常规波束形成法的局限性,虚拟阵元法等超分辨技术日益得到应用.
文献[2]采用单步离散外推法增大阵列的孔径尺寸,有效减小了波束的宽度.文献[3]基于线性预测模型进行孔径的外推和内插,使有效孔径可达实际孔径的2~3倍.文献[4]研究了基于空域四阶累计量的虚拟阵列孔径扩展法,可将阵列孔径扩大1倍.文献[5]采用阵列变换将原始阵列转化为新阵列,新阵列相对原始阵列阵元个数不变,阵元间距得到扩展,从而增大了阵列的有效孔径,但此法需要预估目标的大致方向.文献[6]从内插阵列变换思想出发,将空间进行区域划分,在每个空间区域内得到了具有更大孔径和阵元数的虚拟阵列,从而提高了测角分辨率.文献[7]提出相移虚拟阵元法,利用各阵元接收信号的相位关系,将N个阵元成功扩展到了2N-1个.文献[8]将原始阵列的多个时域输出在空域上扩展为虚拟阵列,理论上可将实际物理孔径扩展数倍.文献[9]分别运用线性最小二乘理论和阵元延迟求和法构造虚拟阵元的接收数据,并通过仿真验证了两者均能一定程度地扩大阵列的有效孔径.文献[10]从理论上分析了将文献[6,9]中的虚拟阵元构造法用于解测向模糊的可行性,并通过仿真试验予以了证明.文献[11]给出了基于遗传算法的虚拟阵元波束形成方法,实现了高指向性的窄波束.近年来提出的新体制雷达MIMO(Multiple-Input Multiple-Onput)雷达,发射端由M个阵元发射不同的正交编码信号,接收端由N个阵元通过匹配滤波将来自不同发射天线的信号进行分离,理论上可产生MN个虚拟阵元[12].
本文研究部署位置不同的多雷达阵列联合超分辨测向问题.在对多个阵列的幅相信号相干处理的基础上,分别采用非线性最小二乘迭代法(NLS,Nonlinear Least Squares)[13]、基于最小熵的反卷积迭代法(IDMEC,Iterative Deconvolution algorithm based on Minimum Entropy Criterion)[14]和最小加权范数法(MWN,Minimum Weighted Norm)[15]构造雷达阵列间的各个虚拟阵元进行超分辨测角处理,对三种虚拟阵元内插算法的性能进行了比较.
多雷达阵列信号的相干处理
1.1 阵列信号的AR模型
如图1所示,设空间有P个相干目标,其方位角分别为 θk,k=1,2,…,P.接收阵列为 N 个阵元组成的均匀线阵,阵元编号为1~N,间距为d.不失一般性,以阵元1为参考,其接收信号表示为

图1 阵列接收信号示意图

式中,uk(t)和φk(t)分别表示第k个信号的包络和初相,则其他各阵元的接收信号可写成

式中,τkn为第k个信号到达第n个阵元时相对参考阵元的时间延迟,表示为
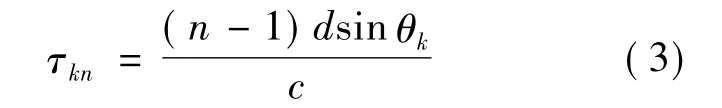
式中c表示光速.
本文假设所有信号均为窄带信号,因此有
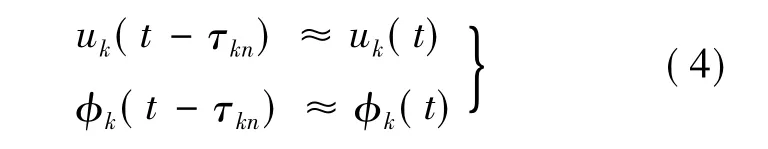
于是有

式中
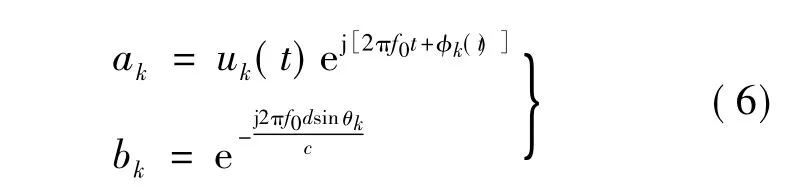
由此可见,阵列的每次快拍接收数据符合AR(autoregressive)全极点模型.
1.2 模型参数估计
式(5)表示的模型由3类参数描述,分别为阶数P,极点bk和复幅度ak.假设模型阶数P已知或已由相关算法估计得到[16],下面讨论极点bk和复幅度ak的估计方法.
对均匀阵列,将每个阵元的接收信号表示为sn(l),n=1,2,…,N,l=1,2,…,L,其中 N 表示阵元数;L表示快拍数.得接收矩阵如下:

式中M表示相关窗长度.
定义矩阵

式中符号H表示共轭转置.
对各Gm进行平滑得相关矩阵

对相关矩阵R应用谱估计算法TLS-ESPRIT[17]可得极点的估计值.
由极点估计值,列极点矩阵

令第l次快拍阵列的接收信号表示为X=[s1(l),s2(l),…,sN(l)]T,其中,符号 T 表示转置.利用线性最小二乘可得复幅度的估计值为

1.3 多雷达阵列信号幅度与相位的相干处理
单部雷达可对目标进行相参测量,独立工作的多部雷达由于自身工作条件不同其测量数据不相干.因此,需对各雷达的测量数据进行幅度校正和相位补偿,使各雷达阵列的接收信号相干[13].
以两个雷达阵列为例.由上文所述方法对阵列1和2分别建立全极点模型,记为M1(dn)和M2(dn),dn表示第n个阵元的位置.以阵列2的接收数据为参照,建立代价函数

式中,A为幅度校正参数,用来补偿幅度差;Δφ为固定相位相干参数,用来补偿固定相位差;Δα为线性相位相干参数,用来补偿线性相位差.
令代价函数C最小可得相干参数的估计值,进而对阵列1的接收数据进行相干补偿,可使两雷达阵列的接收数据相干.
2 虚拟阵元内插算法
本节以图2所示的两个雷达阵列为例,分别讨论NLS,IDMEC和MWN三种虚拟阵元内插算法,多雷达阵列场景可进行类推.假设每个阵列均是阵元数为N、阵元间距为d的均匀线阵,两阵列的中心间距为N'd,并假设阵列的接收数据已得到相干处理.
2.1 NLS 法
设sn为某次快拍下两雷达阵列的接收数据,定义代价函数


图2 两雷达阵列空间分布示意图
式中,n的取值范围覆盖两雷达阵列所有阵元的测量值;qn是加权系数;M(dn)是两阵列的全局全极点模型.
最小化JNLS可得M(dn)的参数估计值,此求解过程实质为一较复杂的非线性最小二乘问题.本文采用信赖域反射算法迭代求解,收敛结果取决于迭代初值的选取.如果初值选取接近全局最优点,算法将会迅速收敛得到满意结果;如果初值选取不合适,将有可能收敛到局部最优点.下面给出迭代初值的一种选取方法.
由上文所述方法分别建立两阵列的相关矩阵R1和R2,构造新相关矩阵

并将由此得到的极点和复幅度的估计值作为迭代初值.
迭代收敛后,得到了两阵列的全局全极点模型M(dn).将各个虚拟阵元的阵元位置代入此模型,即可得每个虚拟阵元上的回波信号值.
2.2 IDMEC 法
对某次快拍的接收数据应用IDMEC法构造阵列间的虚拟阵元,其具体步骤如下:
1)分别建立阵列1和2的全极点模型M1(dn)和M2(dn),并由此估计合成阵列各阵元的初始接收回波数据

2)用测量数据代替估计数据,即

4)利用最陡下降法和最小熵算法优化波束扫描图


式中pr表示概率.
值得注意的是,在整个迭代过程中,步长γ决定了能否收敛及收敛速度.为通过较少的迭代步数较快地达到收敛,可设定γ和初始波束扫描图的平均幅度成比例.
2.3 MWN 法
对某次快拍,分别建立阵列1和2的全极点模型M1(dn)和M2(dn),利用式(15)和式(16)得到合成阵列各阵元的初始回波数据sn,n=1,2,…,N+N',采用周期图谱估计算法得到合成全孔径的波束扫描谱

进行虚拟阵元内插后的全孔径波束扫描谱应相似于式(19)给出的波束扫描谱.为此,采用N维复线性空间加权范数最小化方法,其表达式为
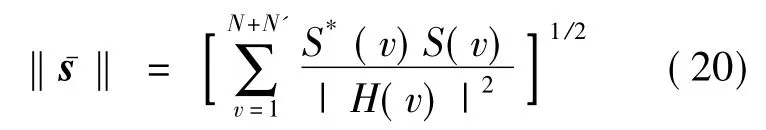
式中,符号﹡表示共轭;s-为全孔径数据估计;S(v)是s-的FFT变换;|H(v)|2等价为角谱域非负权函数.
令|H(v)|2的IFFT表示为ah(n),用ah(n)形成如下循环矩阵:

设Q的Moore-Penrose伪逆为Q+,由Parseval定理与循环矩阵性质可将式(21)等价为
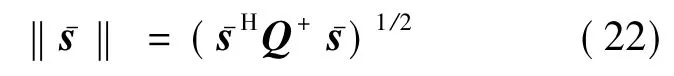
构造虚拟阵元的同时还要保证实际物理阵元的接收信号保持不变,可用线性变换将此过程描述为

式中,W为采样矩阵,其每一行元素在对应的实际物理阵元处为1,其余为0.
因此,应用最小加权范数法进行虚拟阵元内插可描述为在式(23)的约束条件下,求式(22)的最小加权范数解.该解析解的表达式[15]为

实用中考虑到矩阵不可逆的情况,通常采用式(24)的正则解形式,即

式中,ρ为一能使矩阵可逆的小数;I为单位阵.
注意到同前两种虚拟阵元内插算法相比,此法的求解过程不需要迭代.
3 仿真结果及分析
参见图2,假定独立工作的两雷达阵列部署在空间的不同位置,每个阵列的参数设置如下:阵列阵元间距0.5m;阵列阵元数16;雷达工作波长1m.空间存在两个相干目标.假设两雷达阵列的接收信号已经过相干处理.
若两个相干目标的方位角分别为52.5°和55°,其信噪比均为20 dB.阵列间距为200m,快拍数为50.图3给出了应用虚拟阵元内插算法前后基于常规波束扫描得到的角度分辨图,其中图3a~图3d分别表示原始单雷达阵列及分别应用NLS,IDMEC和MWN法进行虚拟阵元内插后的结果图.从图中可以看出,三种虚拟阵元内插算法均能有效地扩展阵列的孔径尺寸,使两目标得到较好分辨.
为研究三种虚拟阵元内插算法的虚拟阵元构造性能,定义构造误差为

图4示出了三种虚拟阵元内插算法的性能对比,图中所示均为100次独立重复试验的平均结果图.其中,图4a~图4d分别表示构造误差与阵列间距、目标间夹角、快拍数和信噪比的关系.考虑到目标相干可能使得两雷达阵列的接收信噪比不一致,图4的每次试验结果均为两相干信号的相位差在0~360°范围均匀变化的平均误差值.

图3 原始阵列和合成阵列的常规波束扫描图
从图4可见:①当两阵列间距变大或两个目标之间的夹角变小时,三种算法的虚拟阵元构造误差均随之变大;②当快拍次数增加或信噪比增大时,三种算法的虚拟阵元构造误差均随之变小;③NLS法的构造误差在目标间夹角较大时小于IDMEC法,在目标间夹角较小时则大于后者;总体上,MWN法的构造误差小于上述两种迭代算法.
为定量研究三种算法的超分辨测角能力,定义测角均方根误差为

式中,θ1和θ2分别表示两目标的真实方位角;和分别表示第i次试验中两目标方位角的估计值;T表示试验次数.

图4 三种虚拟阵元内插算法的构造误差
表1给出了应用不同算法时两目标几个典型方位角下的测角均方根误差值.每个阵列的参数设置同上,两目标的信噪比均为20 dB,快拍数为50,独立试验次数为100.

表1 三种算法的测角均方根误差值 (°)

表2 三种算法的分辨概率
从表1、表2可见:①三种算法中,IDMEC法和MWN法的测向性能基本一致,NLS法的测向性能较差;②由于每个阵元的接收信号的相位影响波束指向,幅度影响旁瓣电平,可推测IDMEC法与MWN法相比NLS法对相位的构造误差较小,而NLS法的虚拟阵元构造误差在目标夹角较大时小于IDMEC法的原因在于对幅度的构造误差较小.
为比较三种算法的运算量,表3列出了它们在Dell Optiplex 755 PC机上运行所需的时间长度.仿真条件同表1、表2.

表3 三种算法的计算时间
从表3可见,MWN法计算时间最短,NLS法和IDMEC法计算时间较长.不难理解,三种算法首先都需求解协方差矩阵并进行特征分解,此步所需的乘法和加法次数相同.但是,MWN法后续无需迭代,因此运算量最小;而NLS法和IDMEC法后续均要反复迭代进行优化,因而运算量较大,且两者的运算量取决于收敛速度,不同条件下它们的运算量大小关系会发生变化.
4 结论
本文对比研究了基于虚拟阵元内插的三种超分辨测向算法,分别采用 NLS法、IDMEC法和MWN法构造雷达阵列间的虚拟阵元以扩大阵列孔径.研究结论如下:
1)三种算法均能有效地增大阵列的孔径尺寸,从而提高测角分辨率;它们的虚拟阵元构造误差均随阵列间距的增大和目标间夹角的减小而增大,随快拍次数的增加和信噪比的增大而减小.
2)在虚拟阵元构造上,MWN法的误差小于NLS法和IDMEC法;在测向性能上,MWN和IDMEC法基本一致,NLS法较差;在运算量上,MWN法较小,NLS法和IDMEC法较大.因此,总体上MWN法优于NLS法和IDMEC法.
此外,应注意到本文的研究对象均为理想点目标,阵列为均匀线阵且阵列流型精确已知.在实际测角中的复杂目标起伏、任意阵列结构和阵列误差等条件下的虚拟阵元构造问题有待进一步探索.
References)
[1] Krim H,Viberg M.Two decades of array signal processing research[J].IEEE Signal Processing Magazine,1996,13(4):67-94
[2] Fan H,El-Masry E I,Jenkins W K.Resolution enhancement of digital beam formers[J].IEEE Trans on Acoustics,Speech,and Signal Processing,1984,32(5):1041 -1052
[3] Swingler D N,Walker R S.Line-array beam forming using linear prediction for aperture interpolation and extrapolation[J].IEEE Trans on Acoustics,Speech,and Signal Processing,1989,37(1):16-30
[4] Dogan M C,Mendel JM.Application of cumulants to array processing-partⅠ:aperture extension and array calibration[J].IEEE Trans on Signal Processing,1995,43(5):1200 -1216
[5] Kim Y-Soo,Kim Y-Su.Improved resolution capability via virtual expansion of array [J].Electronics Letters,1999,35(19):1596-1597
[6] Wang Y,Chen H,Wan S.An effective DOA method via virtual array transformation [J].Science in China,2001,44(1):75-82
[7] Lan Y,Yang S.Virtual array method of beam forming[C]//Xu X.The 2nd International Workshop on Acoustical Engineering and Technology.Harbin:Harbin Engineering University Press,1999:29-30
[8]吴湘霖,俞卞章,李会方,等.基于虚拟阵列的波达方向、载频和极化参数联合估计[J].电子与信息学报,2005,27(12):1887-1891 Wu Xianglin,Yu Bianzhang,Li Huifang,et al.A novel method for joint DOA-carrier-polarization estimation based on virtual array[J].Journal of Electronics & Information Technology,2005,27(12):1887-1891(in Chinese)
[9]胡鹏.虚拟阵元波束形成方法研究[D].西安:西北工业大学航海学院,2006 Hu Peng.Study on beamforming algorithm of array with virtual elements[D].Xi’an:School of Marine Engineering,Northwestern Polytechnical University,2006(in Chinese)
[10]董国英,陶海虹,廖桂生.虚拟阵元解模糊的可行性分析[J].电子与信息学报,2010,32(6):1493 -1496 Dong Guoying,Tao Haihong,Liao Guisheng.The feasibility analysis of ambiguity solving with virtual arrays[J].Journal of Electronics& Information Technology,2010,32(6):1493 -1496(in Chinese)
[11]陈欢,杨德森,张揽月,等.基于遗传算法的声矢量阵虚拟阵元波束形成[J].信号处理,2009,25(10):1498 -1501 Chen Huan,Yang Desen,Zhang Lanyue,et al.Virtual array beam forming algorithm based on genetic algorithm of vector hydrophones[J].Signal Processing,2009,25(10):1498 -1501(in Chinese)
[12] Donnet B J,Long staff ID.MIMO radar,techniques and opportunities[C]//Proc of the3rd European Radar Conference.London:Horizon House Publications,2006:112 -115
[13] Cuomo K M,Piou J E,Mayhan J T.Ultrawide-band coherent processing[J].IEEE Trans on Antenna and Propagation,1999,47(6):1094 -1107
[14] Xu X,Huang P,Feng X.An iterative algorithm for ultra wideband radar imaging from randomly fragmented spectral data[C] //Proc of the 2004 International Radar Conference.Paris:See,2004
[15] Cabrera SD,Parks TW.Extrapolation and spectral estimation with iterative weighted norm modification [J].IEEE Trans on Signal Processing,1991,39(4):842 -851
[16] Akaike H.Modeling by shortest data description[J].Automatica,1978,14(5):465 -471
[17] Roy R,Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Trans on Acoustics,Speech,and Signal Processing,1989,37(7):984 -995
(编 辑:娄 嘉)
Performance comparison among three super resolution direction finding algorithm s based on virtual element interpolation
Chen Wensheng Xu Xiaojian
(School of Electronics and Information Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Three super resolution direction finding algorithms based on virtual element interpolation were studied.On the basis of mutually cohering the signals from multiple smaller arrays of different radars,three super resolution algorithms,namely,the nonlinear least squares(NLS)algorithm,the iterative deconvolution algorithm based on minimum entropy criterion(IDMEC),and the minimum weighted norm(MWN)algorithm were applied to interpolate the virtual elements between the physical radar arrays.As a result,the effective aperture size was increased,thus super resolution direction finding was achieved.Simulations were made to validate the techniques as well as compare the super resolution performance and calculation burden among the three algorithms.Results demonstrate that the MWN algorithm has notonly the lowest virtual element construction error level and calculation complexity,but also the best direction finding performance.Therefore,the MWN algorithm generally outperforms the NLS and IDMEC algorithms.
virtual element;super resolution;direction finding;interpolation
TN 953+.5
A
1001-5965(2011)05-0545-06
2010-01-28
陈文晟(1984 -),男,山西太原人,博士生,chenwensheng@ee.buaa.edu.cn.

