基于退化量分布时序分析的产品寿命预测

王 立 李晓阳 姜同敏

(北京航空航天大学 可靠性与系统工程学院,北京 100191)

基于退化量分布时序分析的产品寿命预测

王 立 李晓阳 姜同敏

(北京航空航天大学 可靠性与系统工程学院,北京 100191)

针对现有性能退化预测方法采用单调回归函数对产品退化随机过程描述不够合理的问题,从产品在各时刻退化量分布角度出发,分析退化量分布参数估计的非平稳时序类型,并对各参数估计分别采用相应类型的非平稳时序分析方法建模,进而给出一种与实际退化随机过程更为相符的基于退化量分布的产品寿命及可靠度预测方法.通过对某电子产品的退化试验,采用所提出的寿命预测方法进行了该电子产品寿命及可靠度预测.结果表明该方法相比传统方法更符合实际.

性能退化;寿命预测;退化量分布;非平稳时序分析

越来越多长寿命高可靠性产品出现,使产品寿命与可靠性评估更加困难.基于产品性能退化信息预测产品寿命及可靠度成为一种有效途径.

目前性能退化预测主要有两种思路:①将性能退化量随时间变化的随机过程各样本函数称为退化轨迹,基于退化轨迹预测.②将性能退化量在不同时刻所服从分布的参数看作随机变量,基于退化量分布进行预测.

现有性能退化预测研究中,文献[1]假设退化量为正态分布进行可靠性预计;文献[2]给出性能退化量分布参数的极大似然估计方法;文献[3]采用退化轨迹函数预测产品性能退化;文献[4]采用线性模型来描述退化量分布参数和退化轨迹.这些文献均将产品退化轨迹或退化量分布参数假设为单调回归函数,进行性能退化预测.然而,实际工程中由于受到环境等因素影响,性能退化量存在随机性及周期性变化,且在这种变化下退化量分布参数往往具有非平稳随机性.现有方法对产品退化随机过程描述不够合理.

非平稳时序包括方差平稳时序和相关系数平稳时序等.非平稳时序分析利用现代统计学和信息处理技术,能充分挖掘非平稳随机时序的自相关性,刻画时序随机性波动规律,是一种适于描述退化随机过程的方法.文献[5]给出基于退化轨迹时序分析的性能退化产品寿命预测方法;文献[6]给出基于退化量分布的性能退化预测时序分析法,但将退化量分布参数时序笼统视为方差平稳随机时序.由于退化量分布不同参数属于不同非平稳时序类型,将所有参数时序笼统视为方差平稳随机时序的假设过于简单,与实际情况不完全相符.因此本文从退化量分布角度出发,对各退化量分布参数,分别采用相应非平稳时序分析方法,进行性能退化产品寿命预测方法研究.

1 退化量分布数字特征分析

产品退化量分布反映了退化随机过程一维分布,其基本数字特征为均值和方差.若各样本退化轨迹为单调回归函数,退化随机过程如图 1.

可知,退化量分布均值和方差为单调回归函数.

然而工程中,由于产品受到各种环境因素影响,实际的退化随机过程如图 2.

图 2 实际退化随机过程

可知,当各样本退化轨迹为随机时序时,退化量分布均值和方差也可能为随机时序.当随机时序具有自相关性时,则时序取值不仅与当前时刻有关,且与其历史时刻取值有关.若仍采用单调回归函数描述退化量分布均值和方差时序,则反映不出退化过程随机波动的自相关性,从而影响退化预测结果.因此,应对退化量分布均值和方差分别采用时序分析方法描述.

2 退化量分布参数估计

本文提出所研究的性能退化过程假设:

假设 1 产品的性能退化过程总体趋势具有单调性,即性能退化总体趋势不可逆.

假设 2 退化过程中,所有产品采样时刻相等.

假设 3 随着时间的变化,退化量分布的类型不变,仅参数变化.

设共有 n个产品样本,以 yt表示产品在 t时刻的性能退化量(或性能退化量的某种非线性变换),以 yti表示 yt的第 i个产品样本.当 yt服从某位置-尺度分布时,任意时刻的位置参数与尺度参数即 yt的数字特征,分别记为 μt和,它们可确定 yt在 t时刻分布情况.例如:

1)当性能退化量服从正态分布时,yt表示性能退化量,其分布参数为 μt和

2)当性能退化量服从对数正态分布时,yt表示性能退化量的对数,yt服从正态分布,其分布参数为 μt和

3)当性能退化量服从形状参数为 θt、尺度参数为 ηt的威布尔分布时,yt表示性能退化量的对数,yt服从极值分布,其分布参数为 μt=lnηt和μt和的估计值可由 yt的样本均值和样本方差得到.由于和是按时间顺序变化的随机变量,因此是时间序列,并且是具有一定退化趋势的非平稳时间序列.

3 退化量分布参数估计平稳性分析

不同类型的非平稳时序建模方法迥异,因此在对退化量分布参数估计采用时序分析方法建模前,必须先进行平稳性分析,以确定退化量分布参数估计的非平稳时序类型.

1)产品样本退化轨迹时序非平稳性分析.

实际工程中,通常认为产品各样本在 m时间段内退化轨迹 yti(t=1,2,…,m)为相互独立的方差平稳时序.由时序分解原理,yti可分为确定性时序 dti和平稳随机时序 rti的叠加.

2)样本均值时序非平稳性分析.

3)样本方差时序非平稳性分析.s2

t时序表达式为

式(3)中第一项为确定性时序.

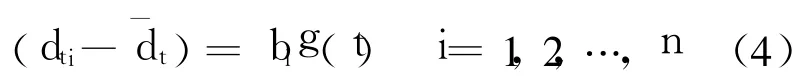
其中,g(t)为关于 t的非零函数;bi为常数.式(3)第二项可表示为

根据文献[7]对相关系数平稳随机过程定义:

定义 1 设{xt,t∈ T}是随机过程,如果

1){xt,t∈T}是二阶矩过程;

2)对任意的 t,t+τ∈T,有

则{xt,t∈T}是相关系数平稳随机过程.

另外再根据文献[8]中的定理:

定理 1 设 xt为相关系数平稳随机过程,则)为平稳随机过程,其中D(xt)=σ2I2(t),σ为常数.

由此,本文给出推论如下:

推论 1 任一非零确定性时序与平稳时序之积为相关系数平稳时序.

证明 设 zt为任一平稳时序,I(t)为任一关于 t的非零函数,即非零确定性时序,则

由此可知 I(t)zt为相关系数平稳时序. 证毕

因此,当 (dti-d-t)满足式 (4)时 ,式 (3)第二项为相关系数平稳时序.

式(3)第三项中,当 rti为正态过程时,(rtir-t)为平稳时序且为正态过程.为常数,并有

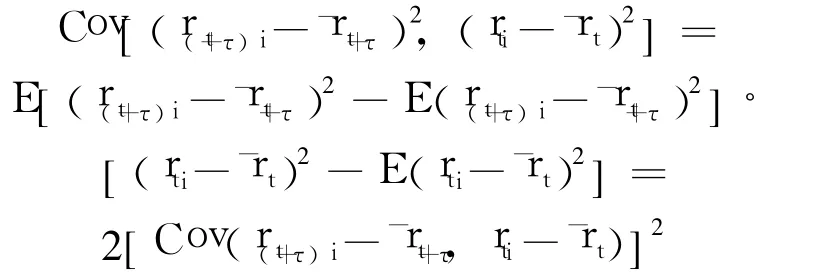
因此,本文仅考虑式(3)前两项,将 s2t时序视为确定性时序与相关系数平稳时序之和.

4 退化量分布参数估计时序建模

产品退化量分布参数估计时序模型是根据产品样本的退化轨迹时序模型推导而得,因此本文首先给出退化轨迹时序的建模方法.

1)产品样本退化轨迹时序建模.

在产品性能退化过程中,产品除自身退化特性外,往往还受到环境及设备因素影响,包括周期性和随机性影响,因此每个样本退化量时序 yti的确定性部分 dti还可进一步分解为单调趋势项 fti和周期项 cti的叠加

fti可采用线性回归函数或可转化为线性的单调非线性回归函数描述为

其中,bi为待定系数;f0i为 fti初值;g(t)为单调非线性函数,当 g(t)=t时,式(7)为线性回归函数.

cti可采用适用于挖掘数据潜在周期性规律的潜周期模型描述,由于同一批受试产品样本所受到的环境及设备影响相同,因此不同样本的周期项 cti理论上也相同,则有

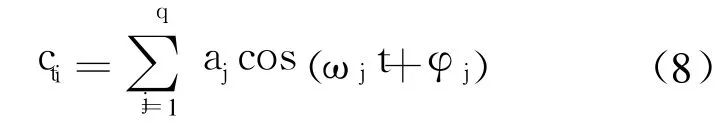
其中,q为角频率个数;λj为角频率;aj为幅值.

rti可采用传统平稳时序分析方法中工程应用广泛、建模简单且适于预测的自回归模型描述为

其中,pi为自回归模型阶数;ηji为自回归系数;εti为白噪声.

2)样本均值时序模型.

y-t具有与样本退化轨迹时序相同表达形式:

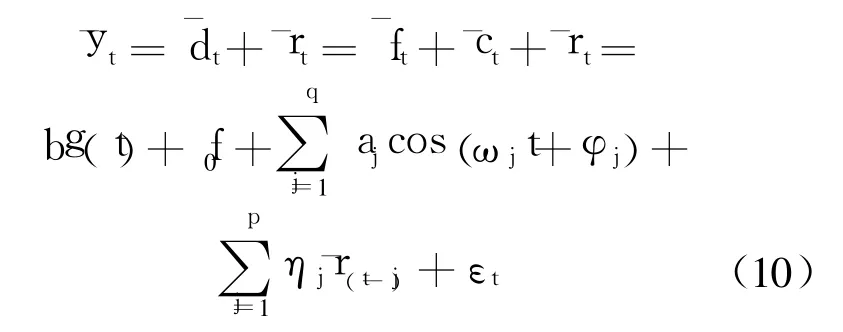
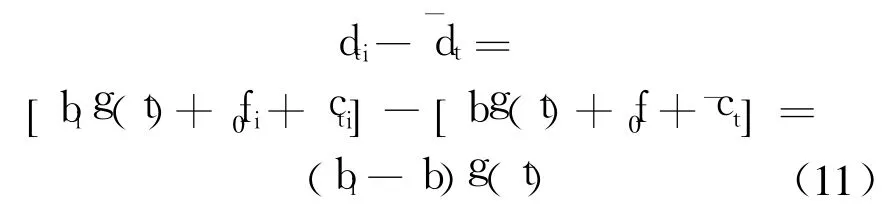
即式(4)满足,式(3)第二项为相关系数平稳时序.

由式(11)可知,式(3)第一项为单调趋势项,以 fst表示趋势项,xt表示相关系数平稳项,有

由式(3)和式(11),fst模型为

其中,bs为待定系数.

相关系数平稳项 xt的模型为

其中,fxt表示相关系数平稳项 xt的确定性部分,称为相关系数平稳趋势项,是关于 t的非零函数;rxt表示相关系数平稳项 xt的随机性部分,称为相关系数平稳随机项,是平稳时序;σr为 rxt的标准差;σxt为 xt的标准差.

由文献[8]可知,σxt可由 xt的绝对值序列|xt|的均值模型得到,即

可知 E|xt|即 fxt,由式(3)和式(11),fxt可采用单调回归函数模型描述为

其中,bx为待定系数.rxt采用自回归模型描述为

其中,px,ηxj,εxt为 rxt的自回归 模型阶数 、自回归系数、白噪声.

5 基于退化量分布的寿命预测

1)退化量分布参数估计时序预测.

根据时序模型最佳(最小均方误差)预测原理,由式(10),y-t的向前 l步最佳预测值为

2)寿命预测.

通过给定某失效阈值 D,可得到 yt在任意时刻到达 D的概率,即产品可靠度 Rt.由第 2节有:

①当性能退化量服从正态分布或对数正态分布时,yt服从正态分布,若 yt随 t单调上升,产品可靠度为

若 yt随 t单调下降,产品可靠度为

②当性能退化量服从威布尔分布时,yt服从极值分布,若 yt随 t单调上升,产品可靠度为

若 yt随 t单调下降,产品可靠度为

此时,产品寿命定义为产品性能穿越失效阈值的概率为 Rt时,所对应的时间 t,而并非产品性能第一次穿越失效阈值的时间.

6 实 例

对同一批次 13个某电子产品进行退化试验,如图 3.对产品施加额定电压,以串联电阻两端电压值作为观测数据.采样间距为 1min.试验共进行了17000min.

图 3 试验设备示意图

由于噪声干扰对非平稳时序分析影响很大,在对试验观测数据进行处理前,应先对其进行滤波处理,以去掉噪声干扰的影响.

经过滤波后的试验观测数据再经初值化预处理后如图 4.

图 4 初值化后的试验观测数据

采用皮尔逊 χ2拟合优度检验方法对各时刻对应的预处理后数据分别进行退化量分布假设检验.根据产品个数,本文取 6个数据量值宽度相等的区间,以保证每个区间包含 2个以上产品样本,则 χ2理论值为 7.815.若 χ2检验值小于理论值,则接受数据分布假设.对该数据所有时刻退化量分布类型的 χ2检验平均值如表 1.

可知,威布尔分布检验不通过,取 χ2检验平均值最小的对数正态分布为退化量分布.

取经过预处理后数据的对数作为退化数据进行本方法的分析,如图 5,黑色平滑曲线为采用幂函数对各产品样本退化轨迹拟合的趋势项.

表 1 退化量分布 χ2检验平均值

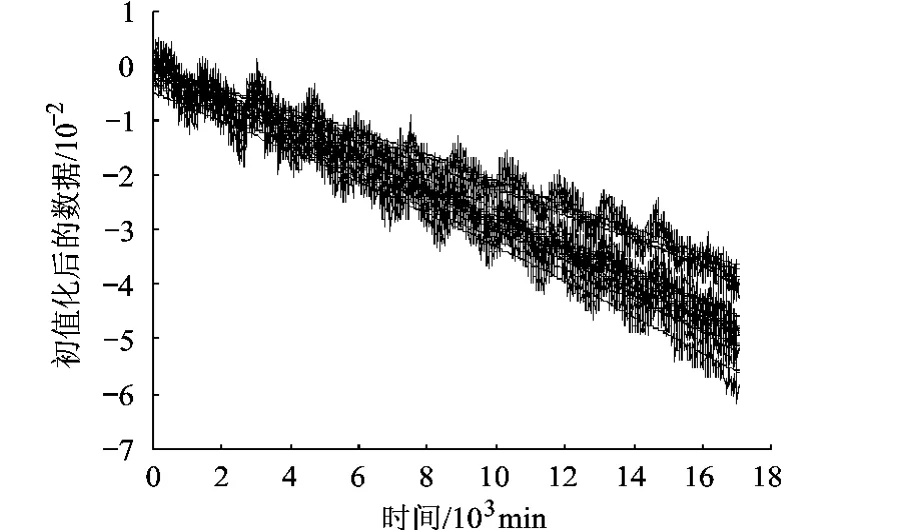
图 5 退化轨迹时序及其趋势项

对退化轨迹时序进行趋势项和周期项建模,减去这两项,得到退化轨迹时序随机项如图 6.

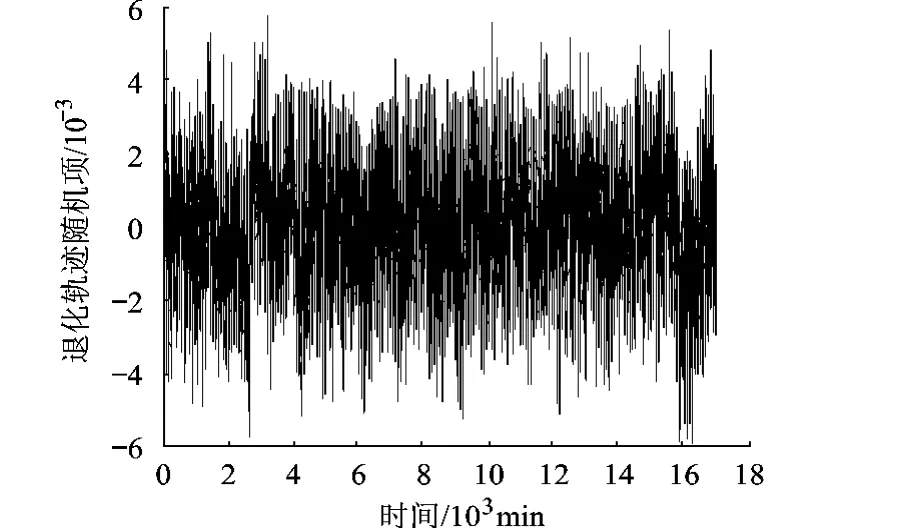
图 6 退化轨迹时序随机项

对退化轨迹时序随机项采用轮次检验法进行平稳性检验.本文将随机项按时间分为 20等份,对各份的均方值进行轮次计算,在 0.05显著性水平下,若轮次数在 64至 125间时,则该数据平稳,各产品结果如表 2.

表 2 退化轨迹时序随机项平稳性检验

可知全部产品退化轨迹时序随机项平稳.则该批产品退化轨迹为方差平稳时序.对随机项采用皮尔逊 χ2拟合优度正态分布检验结果如表 3.

表 3 退化轨迹时序随机项正态分布检验

可知全部产品退化轨迹时序随机项符合正态分布,则式(3)第三项为平稳时序.

分别对退化数据的样本均值时序和样本方差时序进行建模.样本均值时序的趋势项模型为

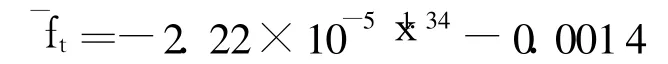
样本方差时序的趋势项模型为

对减去趋势项后的样本方差残差数据进行平稳性检验结果为 57,检验未通过,说明样本方差时序并非方差平稳时序.如图 7.

如图 8,样本方差残差数据绝对值的均值模型为

图 7 样本方差时序残差数据

图 8 样本方差残差数据绝对值及其均值

该残差数据除以其绝对值均值后,再进行平稳性检验结果为 105,检验通过,说明样本方差可视为相关系数平稳时序与确定性时序之和.如图9.

采用第 5节方法,将退化量分布样本均值及样本方差时序预测至 30000min,如图 10、图 11.

根据该电子产品的实际失效情况的经验,取产品失效阈值为初始值的 93%,得到可靠度与寿命关系预测结果.如图 12.

图 9 样本方差相关系数平稳随机项

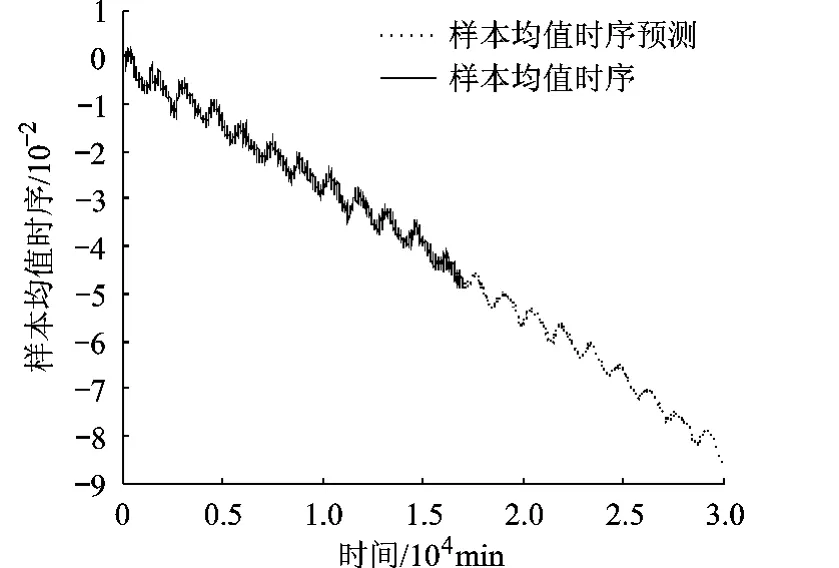
图 10 样本均值时序及其预测

图 11 样本方差时序及其预测

图 12 可靠度与寿命关系预测

可见,采用本文基于退化量分布非平稳时序分析得到的可靠度与寿命关系曲线相比单调回归函数分析方法能反映出退化随机过程的波动性规律.该批电子产品中位寿命预测为 24580min.

7 结 论

本文的研究分析和实例应用表明,对于实际工程中大多数产品,其各样本退化轨迹为非平稳随机时序,则其退化量分布的数字特征往往也为非平稳随机时序.因而本文从退化量分布角度出发,提出样本均值和样本方差时序的非平稳时序分析方法,从而得到反映产品退化随机过程波动性规律的产品可靠度与寿命关系预测.

实际上,这种可靠度随寿命时间的波动性是由于产品可靠度被定义为产品在各时刻退化量穿越失效阈值的概率,在退化量分布数字特征随时间并非单调性变化的实际情况下,产品可靠度也因此不随时间单调下降,而是在单调下降的总体趋势下,还具有一定波动性.这种波动性既包含与当前时刻相关的周期性波动,也包含与历史时刻相关的随机性波动.

由于考虑了产品退化过程中由环境因素引起的周期性和随机性波动,与现有仅考虑产品各样本退化轨迹单调性退化趋势的方法相比,本文方法描述的产品退化随机过程与实际情况更相符.

需指出,本文假设产品的失效阈值为一固定值,然而实际工程中,产品不同样本的失效阈值往往是随机性的.由于产品的失效阈值对产品寿命预测结果影响很大,考虑随机失效阈值的基于退化量分布产品寿命预测方法值得进一步研究.

此外,对于某些产品由于制造费用昂贵,只能得到小样本退化数据的情况,应采用本文第 4节中产品样本退化轨迹时序建模方法,即基于至少一个产品样本的退化轨迹进行产品退化过程描述和寿命预测.对于某些产品由于退化过程过缓,只能在一定时间内能到短时退化数据的情况,可采用加速退化试验的方法,通过提高产品所受的应力水平,加快产品的退化失效过程,从而在较短时间内即可得到更多退化信息.

References)

[1]Jayaram JSR,Girish T.Reliability prediction through degradation data modeling using a quasi-likelihood approach[C]//Proceedings Annual Reliability＆Maintainability Symposium.New York:IEEE,2005:193-199

[2]Huang W,Duane L.An alternative degradation reliability modeling approach maximum likelihood estimation[J].IEEE Transactions on Reliability,2005,54(2):310-317

[3]Wilson SP,Taylor D.Reliability assessment from fatigue micro crack data[J].IEEE Transactions on Reliability,1997,46(2):165-171

[4]邓爱民,陈循,张春华,等.基于性能退化数据的可靠性评估[J].宇航学报,2006,27(3):546-552 Deng Aimin,Chen Xun,Zhang Chunhua,Reliability assessment based on performance degradation data[J].Journal of Astronautics,2006,27(3):546-552(in Chinese)

[5]Wang Li,Li Xiaoyang,Jiang Tongm in,et al.SLD constant-stress ADT data analysis based on time series method[C]//Proceedings 8th International Conference on Reliability Maintainability and Safety.Chengdu,China:IEEE Computer Society,2009:1313-1317

[6]尤琦,赵宇,马小兵.产品性能可靠性评估的时序分析方法[J].北京航空航天大学学报,2009,35(5):644-648 You Qi,Zhao Yu,Ma Xiaobing.Performance reliability assessment for products based on time series analysis[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(5):644-648(in Chinese)

[7]傅惠民.相关系数平稳过程方法[J].机械强度,2002,24(3):400-404 Fu Huim in.Method for correlation coefficient stationary process[J].Journal of Mechanical Strength,2002,24(3):400-404(in Chinese)

[8]傅惠民,刘成瑞,马小兵.时间序列均值和方差函数的确定方法[J].机械强度,2004,26(2):164-169 Fu Huimin,Liu Chengrui,Ma Xiaobing.Method for determining functions of time seriesmean and variance[J].Journal of Mechanical Strength,2004,26(2):164-169(in Chinese)

(编 辑 :娄 嘉)

Life prediction of product based on degradation amount distribution time series analysis

Wang Li Li Xiaoyang Jiang Tongmin

(School of Reliability and Systems Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

For the problem that traditional life prediction methods described product degradation stochastic process inadequately using monotonous regression function,the non-stationary time series types of different degradation amount distribution parameters estimation was analyzed based on product degradation amount distribution at each time.Different parameters estimation was modeled respectively usingnon-stationary time series analysis method.Hence,a realistic product life and reliability prediction method based on degradation amount distribution time series analysis was proposed.A degradation test of a certain electronic product was conducted,and product life and reliability were obtained by the suggested method.The results show that the suggested life prediction method is more reasonable than traditional life prediction method.

performance degradation;life prediction;degradation amount distribution;non-stationary time series analysis

TB 114.3

A

1001-5965(2011)04-0492-07

2010-08-10

国家安全重大基础研究项目(61312803)

王 立(1983-),女,北京人,博士生,xiaolizi1983@hotmail.com.