基于二次加权Mean-Shift的目标实时跟踪
张京爱,李群,李鹏飞,王江涛
(淮北师范大学物理与电子信息学院,安徽淮北235000)
在视频序列中对运动目标进行持续跟踪是计算机视觉的一个重要任务,其被广泛应用在人机交互、智能监控、医学图像处理等领域。目标跟踪的本质是在图像序列中识别出目标的同时对其进行精确定位,为了克服噪声、遮挡、背景的改变等对目标识别带来的困难,出现了很多的跟踪算法。基于区域的跟踪算法通过使一个损耗函数最小化来对连续图像序列间的目标区域进行跟踪,而基于特征的跟踪算法则通过特征抽取(比如亮度、颜色、边缘、轮廓等)来建立模型图像与目标图像间的对应关系,进而确定目标的位置。多数算法采用了统计手段对图像中的被跟踪的区域或像素进行表达,在有参的情况下,目标物体通常假定为一高斯混合模型,通过非线性估计即可获得目标模型的各项参数。然而在实际应用中,高斯混合模型并不适用于实际中多峰、复杂的概率密度情形;与之相比,非参数密度估计手段则能克服高斯混合模型的缺点,对复杂的概率密度进行精确的估计。在非参数密度估计手段中,直方图对于跟踪可变化的非刚性物体具有较好的柔性和鲁棒性,然而由于受到维数的限制(维数随着颜色数目指数增加),其只适合于低维空间,而基于核的密度估计,只要给定足够的样本,就可以适用于低维和高维空间,与前者相比具有更大的应用空间。
Mean-Shift(均值偏移)算法最先由Fukunaga和Hostetler提出[1],其后Comaniciu成功地将其应用于计算机视觉领域中[2-3],近年来,Mean-shift算法以其无需参数、快速模式匹配的特性[4]被广泛应用到目标跟踪领域,其作为一个基于梯度分析的优化算法被有效地用来对目标定位。目前在Mean-Shift框架下的研究主要集中于核窗宽的自适应选择[5-6],以及采用新的目标表达模型和相似函数等领域[7-8];然而对于如何减少算法的迭代次数,增强算法对实时性的适应能力的研究却不多见。本文在介绍和分析基于核密度估计的Mean-Shift跟踪基础上,提出了一种新的偏移向量求解方法,对偏移加权系数进行二次加权,以提高跟踪算法的实时性能。
1 基于核密度估计的模型表达
由于非参数估计方法不需要指明样本所服从的概率密度模型,因而其更适用于样本分布未知的情形,特别是在计算机视觉领域中,很多情况下由于数据在特征空间中不规则的聚类而导致样本的概率密度分布不能用通用的参数估计手段精确的表达,基于核函数的概率密度估计作为最有效的非参数估计手段之一,已被广泛的应用到各个领域中。
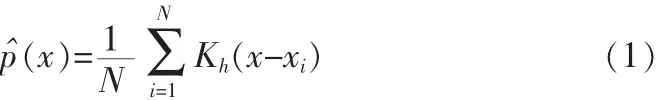
其中Kh为核函数,其窗宽为h,多元情况下,上式可以改写为:
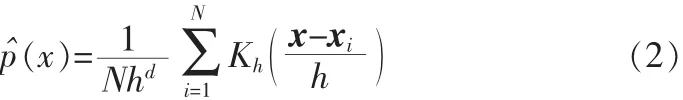
这里x,xi,i=1...N均为d维向量。
假设给定两幅图像,其中一幅包含有被跟踪的目标,称之为“模型图像“,另一幅图像则称之为“候选图像“;目标跟踪的任务就是在“候选图像“中找出被跟踪的目标,并对其精确定位。模型图像中的采样点表示为Ix={xi,ui},此处xi为像素在图像中的二维坐标,而ui则为该像素对应的特征向量。物体的颜色特征因其不易受光照的影响具有较强的鲁棒性,且计算量小的优点,因而采用颜色作为目标的特征空间得到了广泛的重视,本文中模型的特征空间为量化后的颜色空间。候选图像中的采样点表示为Iy={yi,vi}Mj=1,同样给出了采样点的二维坐标和对应的特征向量。将目标的颜色空间量化为m个互不相交的特征子空间,则采样点的坐标和其所属的特征向量可以通过函数b:R2→{1...m}相互关联b(xi),给出了位于xi的像素在量化后的特征空间中所隶属的特征子空间。
假定目标在模型图像中中心坐标为0,且经过正则化后其窗宽为1。采用核函数估计,则颜色u=1...m在目标模型中的概率,即核函数直方图,可以由下式给出:
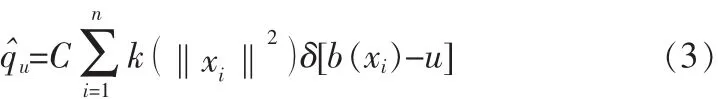
这里δ为Kronecker delta函数,C则为归一化参数,其保

同理,采用同样的核剖面函数k(x),令核窗宽为h,则在候选图像中中心坐标位置为y的核窗口内,其核函数直方图可以表示为:

其中Ch为归一化参数。
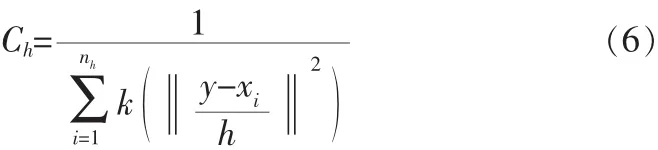
则由式(3)和式(5)可得目标和候选目标的表达模型分别为:
随着信息技术的飞速发展和大数据时代的到来,“徐玉玉案”的发酵、热议,越来越多的传统犯罪模式逐渐转变为新型网络犯罪模式,即利用信息数据进行违法和犯罪活动?
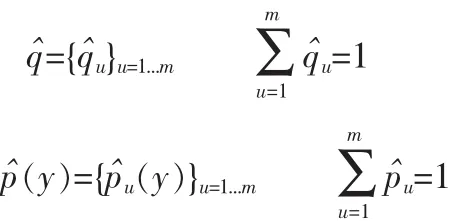
2 Mean-Shift跟踪算法
Mean-Shift算法以其无需参数、快速模式匹配的特性被广泛应用到目标跟踪领域,其通过分析当前区域概率密度的梯度来不断向某个概率密度的极值偏移,最终达到收敛点,该点即为所寻找的模式的位置。采用Mean-Shift算法进行目标跟踪时,首先在第一帧图像中对目标模型进行初始化,然后在相邻图像序列中对目标模型所在位置的周围进行搜索,相似函数最大化的候选区域即为跟踪目标在当前帧中所处的位置。选择一个参照目标模型,然后选择该模型的特征空间,使用该模型在特征空间中的概率密度函数作为其表达。
在前1节中已知目标和候选目标的表达模型为:

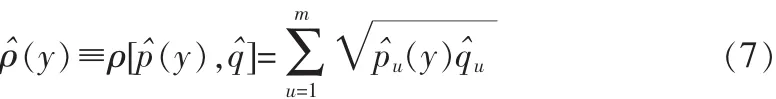

将上式重新写为如下形式:

其中wi为加权系数。
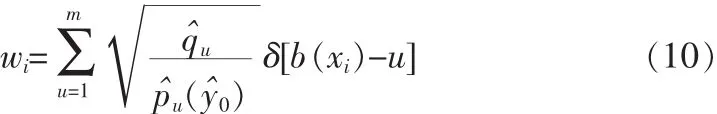
由Mean-Shift算法可得偏移后的坐标位置如下:
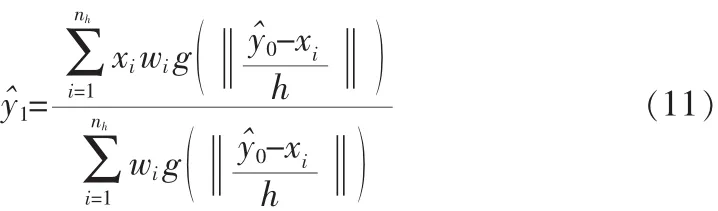
这里g(x)=-k′(x),采用Epanechnikov核,则上式变为:
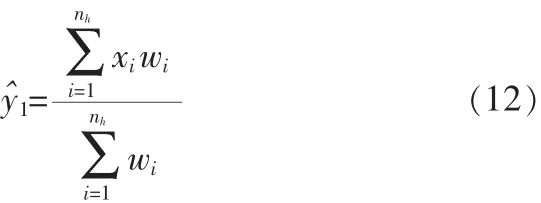
3 算法的分析及改进
当视频序列中目标缓慢运动时,Mean-Shift算法只需要进行一次或少数几次迭代便可对目标进行准确定位;然而当目标运动速度较快,或者目标的核函数直方图维数较低不能高鉴别性的与背景图像进行区别时,算法需要数10次迭代才能对目标收敛,为了克服迭代次数对算法实时性的影响,有必要对算法进行改进以减少均值偏移的迭代次数。
由式(12)可以看出,核窗口的偏移方向跟距离完全取决于加权系数wi,核窗口总是向wi比较大的区域偏移。在当前核窗口所包围的区域与目标模型完全一致时,两者具有相同的特征分布,即=(y)=,此时所有的wi=1,因此偏移量为0,核窗口位置保持不变。然而,当相邻两桢图像中目标位置发生变动时,当前核窗口所包围的区域与目标模型的特征分布存在差异,此时在当前核窗口所包围的区域中目标所处的位置具有较大的权值,而其余背景部分则权值较小,从而使核窗口向目标最可能存在的位置偏移,进而在局部极大值处收敛。图1给出了目标模型位置发生移动时,核窗口内的颜色分布和权值分布的示意图,在图(a)中实线矩形框所示的区域为候选模型所在的位置,而虚线矩形框则给出了当前目标所在的位置,图(b)和图(c)则分别给出了当前桢中候选目标所包含区域的权值和特征分布图,从图中可以看出,目标所在的区域具有较大的权值,而背景区域则权值较小,从而令候选目标的核窗口向权值大的目标区域偏移。

图1 候选目标模型中的特征分布和加权系数Fig.1Feature distribution and weights for candidate target model
显然,要想能够准确地对目标进行识别和定位,目标模型的特征分布要明显的区别于背景以及其他非目标物体的特征分布。在实际应用中,目标模型往往可以表征为一种或几种主要的颜色特征,此时核窗口区域内的像素点在总体上可以由其所隶属的颜色特征来区分是否为目标像素或背景像素。令目标模型所属的主要颜色特征集合为F,则可近似的用如下的判别函数来判断像素点xi是否属于目标模型。

即如果在当前核窗口区域中像素点xi所隶属的特征b(xi)属于集合F,则点xi属于目标模型区域,否则将点xi视为背景区域。
对于属于当前核窗口中的任意像素点xi,有如下定理成立:
证明:
将wnew代入式(12)有:

yc为目标模型的形心,得证。
由上述定理得,可以通过调整式(12)中的权值来加速对目标的收敛,如果令任意f(xi)不为零的像素点的权值重新加权为一足够大的正数,则可以一次性的收敛到目标模型的形心;然而,为了消除非主要颜色特征对目标定位准确度的影响,以更加准确地对目标进行定位,在每一次目标定位时均采用2次迭代来完成:第一次迭代为目标的粗定位,此时采用作为权值求取目标形心的近似位置;然后进行第二次迭代对目标进行精确定位,此时采用wi作为权值进行位置求解,以消除非主要特征对定位准确度的影响,这样每一次偏移仅需要两次迭代即可完成对目标的定位。在实际跟踪中目标物体的主特征和二次加权的权值s在目标初始化时可根据实际经验选定。
4 跟踪试验
为了验证算法的可行性和有效性,对不同的图像序列进行了目标跟踪试验。在采用Mean-Shift算法进行目标定位时,每一次定位均进行2次迭代,第一迭代采用二次加权后的权值wnewi,第二次则使用wi作为权值进行均值偏移求解,跟踪试验中二次加权系数均取s=100。
2次跟踪实验分别采用了PETS04和PETS01视频序列,目标跟踪的结果如图2、3所示。图2给出了PETS04视频序列的跟踪结果,该实验序列长度为100帧,每桢图像大小为384×288,目标核窗口宽度(hx,hy)=(50,70),跟踪目标为对走动的行人,从图中可以看出即使目标突然做快速运动的时候(第452帧至470帧),文中给出的算法仍然能够较为准确的对目标进行定位;图3则给出了PETS01序列的目标跟踪结果,该实验序列长度为50帧,每帧图像大小为768×576,目标核窗口宽度(hx,hy)=(20,50),跟踪目标同样为对走动的行人,在该序列中目标由于对面行驶来的汽车而发生了部分的遮挡,但是跟踪核窗口还是较好地对目标进行了定位。

图2 PETS04序列的跟踪结果Fig.2Tracking results of sequence PETSO4

图3 PETS01序列的跟踪结果Fig.3Tracking results of sequence PETS01
由上述两个不同视频序列的跟踪结果可知,本文提出的算法具有较高的准确性和可行性。与文献[3]中的算法相比,本文的算法在对目标进行较为准确的定位的同时,每次定位仅需要2次迭代,要明显少于[3]中的平均4次迭代。
5 结论
本文提出了一种基于Mean-Shift的目标跟踪新方法。在新方法中,通过对均值偏移的原理进行阐述,分析了偏移向
量与其权值之间的关系,根据不同的颜色特征与目标之间的联系对偏移向量的权值进行了二次加权,这使改进后的算法更加有效,只需2次迭代便可对目标进行准确定位。实验结果表明,与经典的Mean-Shift跟踪算法相比,该算法在保证了准确性的同时具有更好的实时性能。
[1]Fukunaga K,Hostetler L D.The estimation of the gradient of a density function,with applications in pattern recognition[J].IEEE Transaction on Information Theory,1975,21(1):32-40.
[2]Cheng Y.Mean shift,mode seeking,and clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1995,17(8):790-799.
[3]Comaniciu D,Ramesh V,Meer P.Kernel-based object tracking[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2003,25(5):564-577.
[4]Comaniciu D,Meer P.Mean shift:A robust approach toward feature space analysis[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2002,24(5):603-619.
[5]Collins R.Mean-shift blob tracking through scale space[C]//In Proceedings of IEEE Computer Society Conference on ComputerVisionandPatternRecognition(CVPR’03),2003:234-240.
[6]Bradski G R.Computer vision face tracking as a component of a perceptual user interface[C]//In Proceedings of IEEE Workshop on Applications of Computer Vision,1998:214-219.
[7]Elgammal A,Duraiswami R,Davis L.Probabilistic tracking in joint feature-spatial spaces[C]//In Proceedings of the IEEE Computer Society Conference on Computer Visionand Pattern Recognition(CVPR’03),2003:781-788.
[8]YANG Chang-jiang,Duraiswami R,Davis L.Efficient Mean-Shift tracking via a new similarity measure[C]//In ProceedingsofIEEEComputerSocietyConferenceon Computer Vision and Pattern Recognition(CVPR’05),2005:176-183.

