多约束条件下三维最优末制导律及仿真研究
吕永佳,张合新,黄金锋,吴玉彬,李正文
(第二炮兵工程学院陕西西安710025)
飞行器在攻击目标时,不仅希望得到最小的脱靶量,还希望命中目标时弹体姿态最佳,从而使战斗部能够充分发挥最大效能,取得最佳毁伤效果。近些年国内外提出许多带落角约束的末制导律,既包括经典方法,如比例导引律,还包括利用现代控制理论设计的导引律,如神经网络导引律,模糊导引律、最优滑模导引律等。
对地攻击末制导过程中,在考虑命中目标有落角约束条件和保证机动速度损失最小的条件下,三维最优制导律是目前较好且广泛采用的一种制导方案[1-2]。本文以最优控制为基础,考虑末端角约束条件,运用二次型最优推导出一种最优制导律,在保证速度较小的前提下大大提高了该飞行器的毁伤效果。并对典型算例进行数学仿真,运用典型弹道仿真验证了该制导律的可行性和良好的弹道性能。
1 问题的描述
以目标和飞行器质心为基准,将飞行器的运动分解为俯冲平面和转弯平面内的运动[3-4]。其中,俯冲平面定义为飞行器质心和目标连线所确定的平面,转弯平面定义为过目标和飞行器质心而垂直于俯冲平面的平面。基于飞行力学原理,转弯平面内的运动可视为小量[5]。所以在确定飞行器再入运动制导规律时,可将俯冲平面与转弯平面的运动分开来进行研究。为了方便研究导引规律,选取视线坐标系作为末制导过程的控制坐标系。视线坐标系与地面坐标系之间的关系由高低视线角和方位视线角来确定。以俯冲平面(如图1所示)内的运动为例,建立基于视线角速率的标称运动方程为
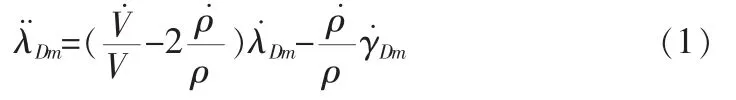
其余各符号含义参见文献[6]。
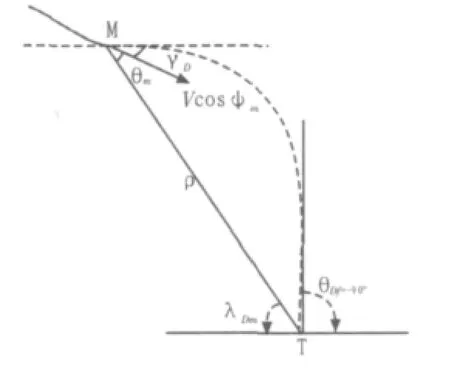
图1 俯冲平面控制示意图Fig.1Schematic diagram for the dive plane control
2 多约束条件下三维最优末制导律
在俯冲平面内,终端时刻飞行器的约束条件为λ˙Dm为零,同时视线角λDm等于预定落角(弹道倾角)的大小,即

如果令

由于速度V远大于速度大小变化率V˙,因此假设V˙/V≈0,Tg=-为剩余飞行时间,得
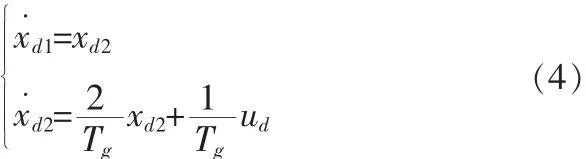
令
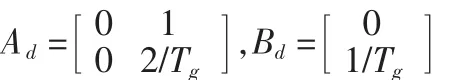
则状态方程可改写为

这是一个变系数非齐次线性微分状态方程组,控制任务为在有限时间tf内使得xd1(tf)=0,xd2(tf)=0。选择上述终端条件及制导过程中能量消耗最省作为约束条件,选择二次型指标为:
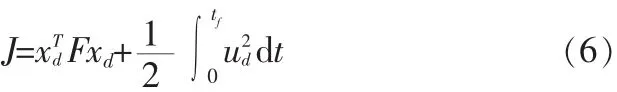
根据最优控制理论,基于上述线性系统二次型性能指标的最优导引律为[6]

同俯冲平面类似,转弯平面的最优导引律为

3 三自由度仿真及结果分析
三自由度动力学方程见文献[6],在仿真时可以假定γc=0,根据某型飞行器的飞行特点,在末制导段m=1 050,ρ0=1.29,β=1/72 001,s=0.6,飞行器的初始位置为(-5 000,8 500,2 m),目标位置(0,0,0 m),飞行器末制导的初始速度为1 200 m/s,为了使某型飞行器有最大的毁伤效果并结合该飞行器的战术指标要求,圆概率偏差CEP≤3 m,限定速度落角为rDF=-80°,rTF=0°,纵向过载、侧向过载分别限定要研究制导律对制导精度的影响,在仿真时将姿态控制系统视为理想环节。
1)构建三自由度仿真模型如图2所示。
2)仿真结果如图3所示。
图3表明,飞行器在本文所设计的多约束条件下三维最优末制导律的控制飞行下,CEP=0.83,λDm(tf)=79.97,λTm(tf)=0,不仅满足落点精度、飞行时间、能量消耗的要求外,还满足入射的高低角、方位角等末端角约束条件。
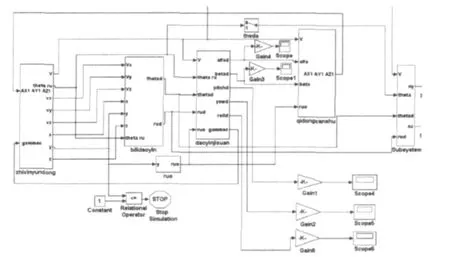
图2 三自由度仿真模型Fig.2The mode of 3 DoFs simulation
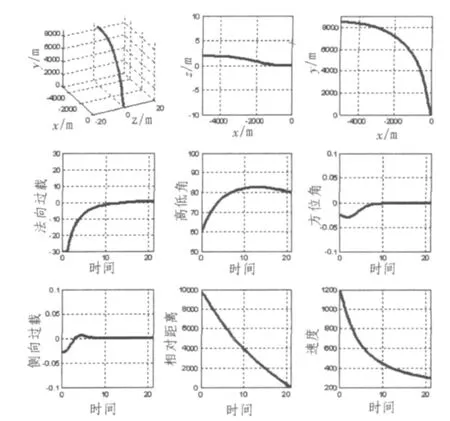
图3 仿真结果Fig.3Simulation results
4 结论
本文综合考虑脱靶量、落角、入射角等多约束条件,在建立在准确参数模型和精确估计剩余飞行时间基础上运用二次型最优黎卡提方程推导出多约束条件下三维最优制导律,通过典型弹道仿真试验验证,该制导律不仅能够满足落角、入射方位角等约束条件下的高精度制导,而且对弹道早期修正能力较强,在末端落角、入射角裕度较大,弹道相对平稳。因此该末制导方案是有效的。
[1]孙未蒙,郑志强.多约束条件下对地攻击的最优制导律[J].兵工学报,2008,29(5):567-571.SUN Wei-meng,ZHENG Zhi-qiang.Optimal guidance law with multiple constraints in ground strike[J].Acta ArmamentarII,2008,29(5):567-571.
[2]陈克俊,赵汉元.一种适用于攻击地面固定目标的最优再入机动制导律[J].宇航学报,1994,1(1):1-7.CHENKe-jun,ZHAOHan-yuan.Anoptimalreentry maneuver guidance law applying to attack the ground fixed target[J].Journal of Astronautics,1994,1(1):1-7.
[3]Dns P G,Radhakant P.Nonlinear model predictive spread accelerationguidancewithimpactangleconstraintfor stationary targets[C]//The 17th World Congress Proceedings of the International Federation of Automatic Contr01,Seoul,Korea,2008:13016-13021.
[4]LU Ping,Doman D B,ScMerman J D.Adaptive terminal guidance for hypervelocity impact in specified direction[R].AIAA,2005:2005-6059.
[5]Innocenti M,Pollinl B,Tuna D.A fuzzy approach to the guidance of unmanned air vehicles track·ing moving targets[J].IEEETransactionsonControlSystentsTechnology,2008,16(6):1125-1137.
[6]赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997.

