导弹水下热发射出筒过程流动特性①

曹嘉怡，鲁传敬，2，陈 鑫，李 杰，陈 瑛

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240;2.海洋工程国家重点实验室，上海 200030)

0 引言

导弹垂直发射系统，按照初始动力可分为冷发射和热发射2种方式。冷发射方式利用活塞或压缩气体(压缩空气、火药燃气)产生推动导弹的动力，把导弹从发射筒中弹射出去。热发射方式利用导弹自身携带的发动机或助推火箭产生起飞动力，不依赖其他外来力量。热发射将发射筒弹射与发动机水下点火集为一体，这一发射方式不仅大大简化了整个发射系统和水下发射程序，而且能大幅提高导弹的出筒速度。

国内对导弹水下发射的研究以实验为主，关于水下发射流场结构与流动特性的理论分析与数值模拟研究的文献不多。鲁传敬等［1］研究了导弹喷气推进垂直上升运动，提出了水和燃气流动与导弹运动的耦合求解方法，进行了数值模拟。王诚［2］对有动力发射导弹发射过程中高温燃气与作用的燃气泡进行了研究。黄建春、叶取源等［3］采用基于质量和能量守恒的零维燃气泡计算模型，对水流场、喷管流场和燃气泡流场进行耦合求解。王诚、叶取源和何友声［4］采用了一维非定常气流场模型和轴对称理想水流场模型，对水下发射导弹的尾部非定常燃气泡内外流场进行了耦合数值求解。考虑了高温燃气与水介质之间的传热、汽化等，其对泡内气体流动的影响。仲峰泉，陆夕云等［5］对喷管内高温燃气的推进和气囊演变过程提出简化的模型，并进行了非定常可压缩Navier-Stokes方程的数值模型。单雪雄等［6］研究了带有摆动喷管的导弹水下发射时燃气流场与水流场的相互干扰。王晓宏等［7］定性研究了水环境的惯性对水下喷管内气体流动造成的阻滞作用。李悦等［8］针对燃气发生器喷喉面积对导弹发射动力的影响，进行了导弹运动参数、内弹道性能的计算与分析。这些计算模型都相对较简单，且做了较多的简化，不能详细描述实际导弹发射过程中的各种详细特征。近期，曹嘉怡等［9］对潜射导弹垂直发射出筒过程中的发射筒内流场特性进行了数值模拟，其外部流场采用了简化模型。刘筠乔等［10］将通气空泡技术用于导弹水下垂直发射，对发射筒内流场进行了简化，研究了出筒过程中导弹的流体动力特性和通气空泡的演化。

本文针对导弹水下热发射这一复杂问题，建立了较完整的计算模型。考虑了高温燃气与水之间发生的传热、传质等复杂现象，并对导弹出筒过程中的发射筒内外气-水流场及弹体运动轨迹进行了耦合计算，得到了较完整的流场计算结果。

1 数学模型

1.1 控制方程

本文研究的导弹水下热发射出筒过程流场，涉及气液两相混合流动，是一个瞬变多相流问题。采用Mixture模型来模拟这一两相流动问题，该模型采用单一流体假设，用体积分数α(0≤α≤1)表征控制体积中某一相的占有率。模型的控制方程如下［11－12］:

(1)连续性方程

其中，混合相的密度和速度定义为

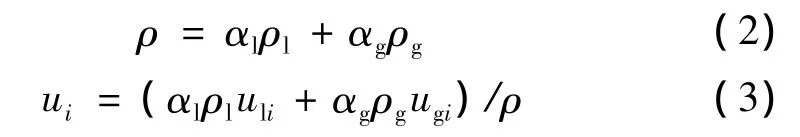
其中，l和g分别表示液相和气相。气液两相的体积分数具有下列关系:αl+αg=1。

(2)动量方程

其中，Fi为体力项，本文为重力。混合项的粘性系数定义为 μ =αlμl+ αgμg。

(3)能量方程

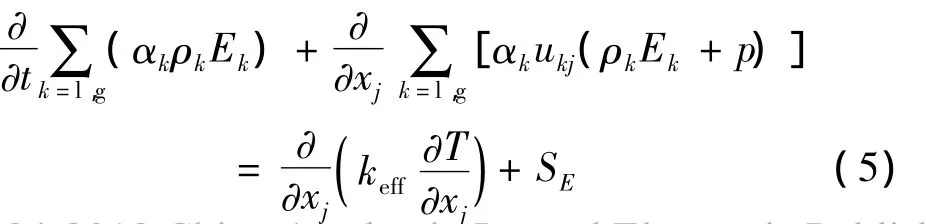
其中，keff是有效热传导率(k+kt)，这里kt是湍流热传导率，由使用的湍流模型定义。

(4)状态方程

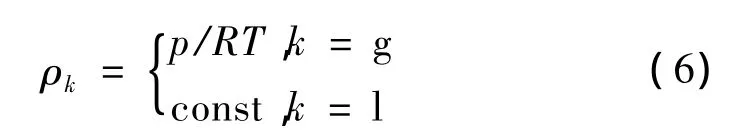
Fluent的两相流模型中，只能有一项为可压缩相，故这里取气体为可压缩项。

(5)体积分数的输运方程

1.2 湍流模式

考虑本文研究对象的特点，本文采用了标准k-ε模型。这种湍流模型适合完全湍流流动，是一种针对高Re数的湍流计算模型［13］。

(1)湍流动能方程(k方程)

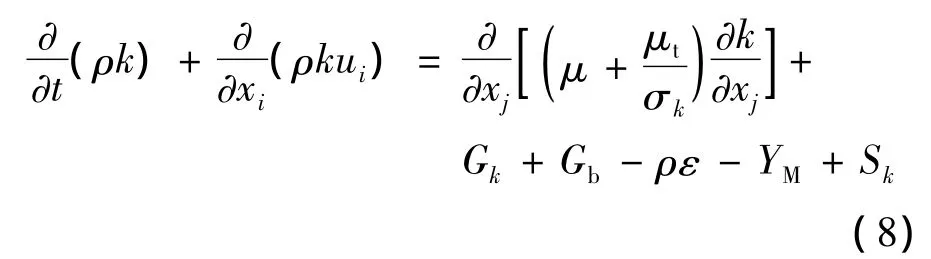
(2)湍流能量耗散率方程(ε方程)

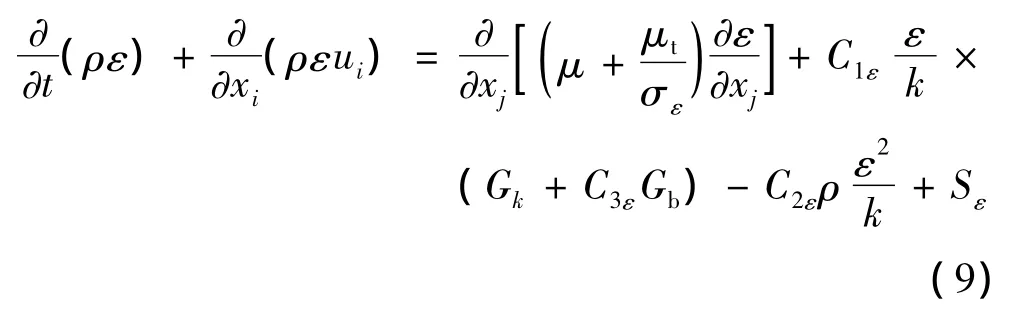
式中 Gk为因时均速度梯度产生的湍流动能;Gb表示由于浮力产生的湍流动能;YM体现了可压缩性;C1ε、C2ε、C3ε是常数;σk和 σε分别为 k 和 ε 的 Prandtl数;Sk和Sε是用户定义的源项。

1.3 弹体运动方程

发射过程中导弹受力由重力G、喷管推力FN和气、水流场对弹体作用力FL组成，其中FN和FL由每个时间步流场计算所得物理量积分得出［9］。设导弹质量为m，则出筒过程中导弹的运动方程为

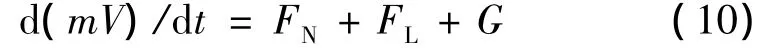
1.4 数值求解方法

本文运用CFD软件FLUENT，对导弹水下热发射出筒过程进行了数值求解。采用Mixture两相流模型，用有限体积法对控制方程进行离散，利用SIMPLE算法对非定常流场进行求解。采用了动网格技术解决导弹发射过程中运动边界和计算域变化的问题，并用C++语言编写了自定义函数模块(UDF)，实现了气水流场与导弹运动的耦合求解。

1.5 计算模型

本文所模拟的导弹水下热发射方案为垂直发射，假定所考虑的导弹发射过程为轴对称流动，取对称轴为x轴，其方向为重力方向。模型外形如图1所示，发射筒由内外套筒组成。

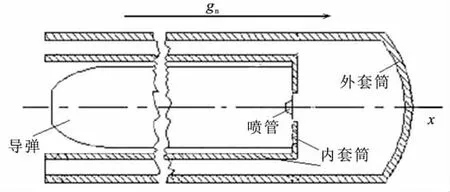
图1 导弹水下发射装置简易外形图Fig.1 Summary outline of missile underwater launcher

图2为计算模型示意图。初始时刻喷管喉部位于坐标原点处，喷管喉部有堵片把喷管隔成两部分，发射筒内、外套筒出口处，有薄膜将发射筒内外流场隔开，当堵片和薄膜两侧压差达到一定值时，堵片和薄膜破裂。初始时刻，喷管堵片左侧充满压强为1 atm的理想气体，堵片右侧及发射筒内充满压强大小为发射筒出口处水压的气体。发射筒外为重力作用下的静止水流场，水流场左面和上侧为压强条件，右侧为固壁面条件。喷管入口处条件由燃烧室总温、总压条件给出，如图3所示。

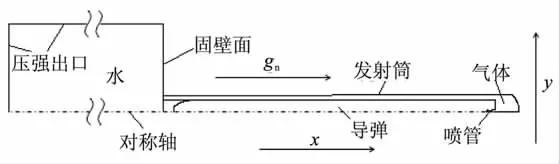
图2 计算模型Fig.2 Computation model

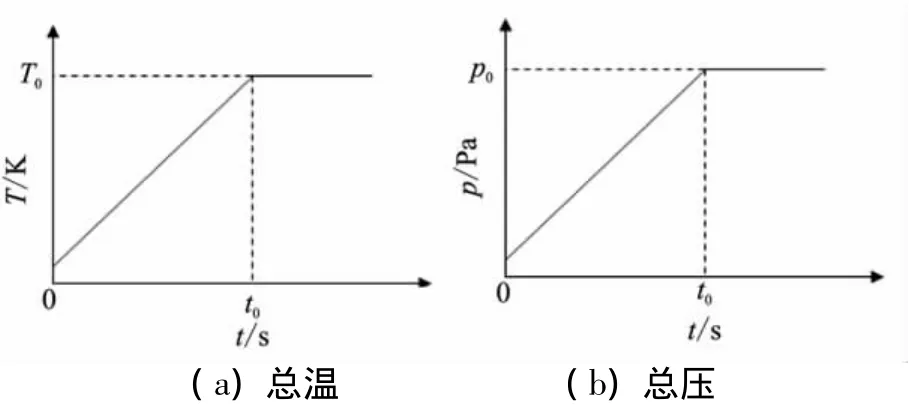
图3 燃烧室总温、总压条件Fig.3 Total temperature and pressure of combustor

2 计算结果与分析

计算结果表明，发动机点火后喷管喉部处堵片在0.007 s时刻被吹掉，内、外套筒堵片在0.063 5 s时刻被吹掉。图4为导弹在发射筒内及出筒一段时间后的位移、速度和加速度随时间变化图，0.848 7 s时刻弹底脱离发射筒。图4中，L为弹长，¯v为速度平均值，¯a为加速度平均值。

图4 导弹运动的位移、速度、加速度与时间的关系Fig.4 Displacement，velocity and acceleration of missile motion vs time

图5、图6分别为导弹出筒过程中，导弹受力和喷管推力与时间关系图。其中，¯P为合力平均值，¯FN为喷管推力平均值。可看到，弹体在发射筒内时受到气体推力不断加速，当弹底脱离发射筒后，由于气体压强的释放，弹体受力减小，在航行一段距离后，开始做减速运动。分析图4～图6，发现0.93 s左右弹体的加速度和受力有突变。这是由于喷管的工作状态为过膨胀状态，当弹底脱离发射筒，尾部射流区进入水流场后，环境压强大于激波前低压区，射流前区产生颈缩现象，激波面向喷管内回推，造成喷管出口物理量突变，见图7，关于这一现象可参考文献［14］。射流这一非定常现象会影响发动机工作效率，使弹体受力产生振荡。

图8为喷管入口下游轴线上不同时刻的马赫数和压强分布图。¯Pe为喷管入口压强。初始时刻，由于弹底离发射筒底部较近，喷管所喷出的高温、高压气体对发射筒底部影响较大，在发射筒底部形成了高压区域。随着弹体不断爬升，高速射流对发射筒底部影响减弱。当弹底脱离发射筒后，发现喷管射流的超音速混合区缩短了，这是由于外围水流场的粘性较大，射流与外围水介质发生大量动量交换，使射流能量减少，轴向速度下降较快。

图5 弹底、弹头受力及导弹合力随时间变化图Fig.5 Time evolution for the force of missile bottom，missile head and the total force of missile

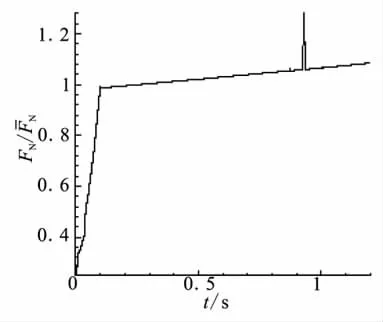
图6 喷管推力随时间变化图Fig.6 Time evolution for thrust of nozzle

图7 0.93 s时内激波位置和喷管附近燃气射流形态Fig.7 Contour of shock wave location and gas jet at 0.93 s

图9为导弹出筒过程中的相位演变过程。观察到初始时刻，弹头整个被从发射筒内外泄的气体所包围。随着弹体不断爬升，一部分从发射筒内溢出的气体，也会附着在弹体上，上升一段距离。当弹体离开发射筒后，由于外围水流场的滞止作用，发射筒内气体很难立刻向外排出，但随着筒内气体压强的释放，在弹体离开发射筒一段距离后，筒外的水介质开始向筒内倒灌，影响筒内气体流场，如图9中1.0 s时刻流场相位分布。随着发射筒外水介质的不断涌入，筒内大部分气体很快被挤出筒外，部分气体被挤向外套筒。当涌入的水介质到达内套筒底部，通过内外套筒间的排气孔进入外套筒时，会形成一股气水混合的高速射流，对外套筒底部形成很强的冲击载荷，如图9中的1.0 s和1.2 s时刻。由于发射筒内的气体被密度较大的水介质所替换，发射筒内压强也有所升高。

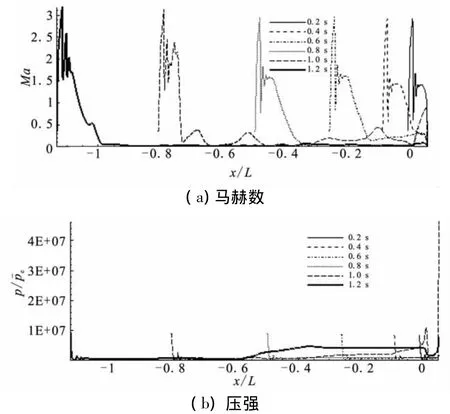
图8 不同时刻轴线上马赫数和压强分布Fig.8 Distributions of pressure along the axis at various times

图9 不同时刻流场相位分布图Fig.9 Phase distribution at various times

3 结论

(1)导弹在发射筒内时，由于发射筒内气体不断积聚，弹体在推力作用下加速爬升，当弹体脱离发射筒进入水流场后，随着尾部气体压强的释放，弹体受力减小，并在航行一段距离后作减速运动。

(2)由于喷管处于过膨胀状态，当导弹完全进入水流场后，环境压强大于激波前区压强，使射流产生颈缩和激波回推现象，造成发动机工作状态不稳定，弹体受力产生振荡。

(3)针对双套筒发射结构，当弹体脱离发射筒后，随着筒内气体压强释放，外围水介质涌入发射筒，并随着水介质的灌入，会在内外套筒连接处形成一股高速气水混合射流，从而在外套筒底部形成高压载荷。

［1］鲁传敬，陈方，樊泓，等.导弹水下点火的流体动力研究［J］.航空学报，1992，13(4):B124-B130.

［2］王诚.燃气泡的计算［D］.上海交通大学，1992.

［3］黄建春，叶取源，朱世权.不同发射深度下导弹水下点火气水流体动力计算［J］.应用力学学报，1994，11(3).

［4］王诚，叶取源，何友声.导弹水下发射燃气泡计算［J］.应用力学学报，1997，14(3):1-7.

［5］仲峰泉，陆夕云，庄礼贤.火箭水下发射复杂流场的近似数值模拟［J］.宇航学报，2000，21(2):1-7.

［6］单雪雄，杨荣国，叶取源.具有推理矢量控制系统的导弹流体动力［J］.上海交通大学学报，2001，35(4).

［7］王晓宏，陈义良，李潜，等.导弹水下发射时喷管的气体流动［J］.推进技术，2001，22(1):61-64.

［8］李悦，周儒荣.燃气发生器喷喉面积对导弹发射动力的影响［J］.南京航空航天大学学报，2004，36(3):353-357.