AZ31镁合金早期力学性能退化非线性超声检测

吴 斌, 颜丙生, 何存富, 焦敬品

(北京工业大学机械工程与应用电子技术学院,北京 100124)

金属零部件由于承受载荷而产生力学性能退化,其寿命一般可分为三个阶段：早期的力学性能退化(位错群的大量产生以及驻留滑移带(Persistent slip bands,PSBs)和微裂纹的形成)、损伤的起始与积累(微裂纹的成核长大和宏观裂纹的产生)以及最后的断裂失效[1]。对于设计良好的结构元件,第一和第二阶段一般占整个寿命的 80%～90%[2],因此发展金属材料早期力学性能退化的有效检测和评价手段就显的十分重要。

超声无损检测技术利用波的时程、声速和衰减等物理参数已经可以对构件寿命的第三阶段进行有效的检测和评估[3]。但是,上述线性物理参数对材料和结构早期力学性能退化并不敏感[4]。近期相关实验研究表明金属材料的早期力学性能退化与超声波的非线性效应密切相关[5-10]。在金属材料的早期力学性能退化阶段,由于位错和滑移带等微观缺陷的存在,当单一频率的超声波在金属材料内部传播时会使波形发生畸变,从而产生高次谐波。因此,通过对这些高次谐波的检测,可以对材料和结构的早期力学性能退化做出有效的无损检测和评估。

非线性超声无损检测技术一直是研究的热点。Nagy PB[4]通过实验比较了超声线性和非线性参数对材料疲劳失效的敏感程度。指出随着疲劳次数的增加,非线性系数明显增加,但是线性参数(衰减、声速等)却没有发生明显变化。Yost and Cantrell[7]从实验上验证了疲劳引起的位错对超声非线性系数的影响。Kyung-Young Jhang[6]采用一维纵波模型,使用PZT探头离线检测了铝合金材料的非线性系数,得出了二次谐波和非线性系数都随疲劳次数增加的结论,但实验结果有较大的分散性。Jin-Yeon Kim等[9]用PZT探头对镍基合金疲劳损伤的超声非线性行为进行了实验研究,主要是对实验系统进行了优化,分别离线测量了低周和高周疲劳试件的非线性系数,指出高周疲劳的实验结果分散性更大。徐从元等[11]用压电换能器测定了四个不同疲劳损伤程度下LY-12铝合金棒的非线性系数、声速和衰减。根据测量结果指出疲劳引起的声速和衰减的变化远小于非线性系数的变化。税国双等[12]对非线性超声无损检测技术的研究现状进行了综述,指出了非线性超声在金属疲劳检测中的应用前景。

尽管非线性超声无损检测技术具有广阔的应用前景,但仍然没有成功地应用于工程实际。针对镁合金构件在复杂工作条件下抗疲劳性能差的问题[13,14],发展了一套可靠的超声非线性系数测试实验系统,利用该系统进行了镁合金拉伸和疲劳非线性超声检测实验,并对拉伸试件进行了原位微观观察。

1 超声非线性理论

由于固体介质的材料非线性,单一频率正弦超声波将与固体介质间产生非线性相互作用,从而产生高次谐波,为了有效反应这一特点,Cantrell,Breazeal等人[15]建立了固体介质内的非线性超声波动方程：

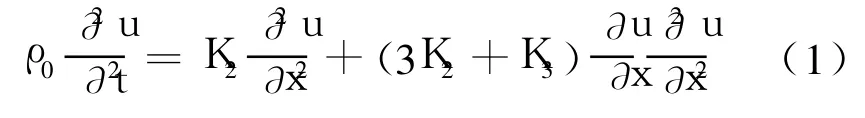
其中ρ0为介质密度,K2为二阶弹性常数(second-order elastic constants,SOE),且K2与纵波波速的关系有K2=ρ0c2,K3为三阶弹性常数(third-order elastic constants,TOE)。若定义非线性系数为[16,17]：

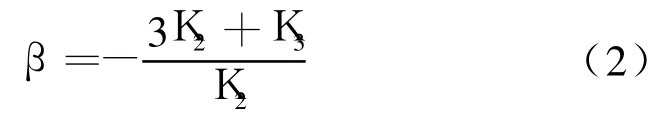
并设方程(1)的初始条件为：

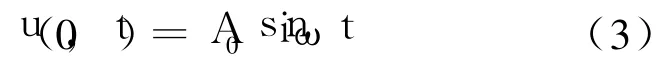
用逐级近似微扰法可求得方程(1)的解为[15]：

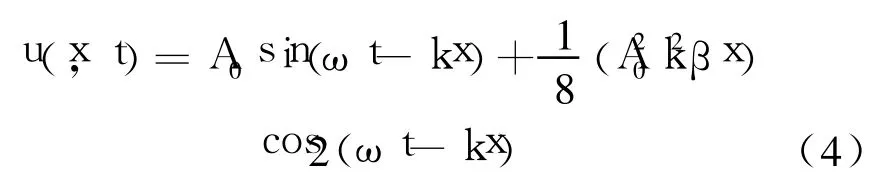
其中k=ω/c为波数。由(4)式可知,基波幅值为：

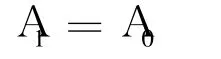
二次谐波幅值为：

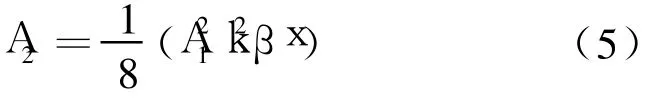
进而可以得到材料的非线性系数为：

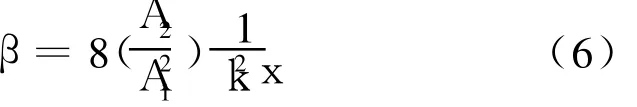
根据方程(6),对于给定的声波频率和波传播距离,通过对基波和二次谐波幅值A1和 A2的测量,就可以确定材料的超声非线性系数。

固体材料的非线性主要来自两个方面：(1)构成材料的原子间相互作用力(或点阵)的非简谐性; (2)材料内部的位错、滑移带和微裂纹等微观缺陷。研究表明,由位错等微观缺陷引起的非线性比由原子点阵的非简谐性引起的非线性大得多[2]。金属作为一种晶体,其力学性能退化与其中位错的运动存在密切的关系,周期性疲劳载荷的作用下,金属材料内部的位错弦长、位错密度、位错组态和滑移带等微观结构将发生变化,从而使超声非线性系数有较显著的改变[18]。因此超声非线性系数 β可以用作描述介质非线性的量化指标,特别是对材料的早期疲劳寿命预测将具有重要的实际意义。

在本实验中,为了研究方便,采用 β=A2/A21来表征超声非线性系数的变化情况。显然,它与材料的绝对非线性系数成正比。

2 实验系统与测量方法

图1所示为超声非线性系数测量系统。系统主要包括信号发生器 33220A、功率放大器 AG1016, MTS810材料疲劳实验机、高能低通滤波器、衰减器、传感器、示波器、计算机以被检测试件和夹具。

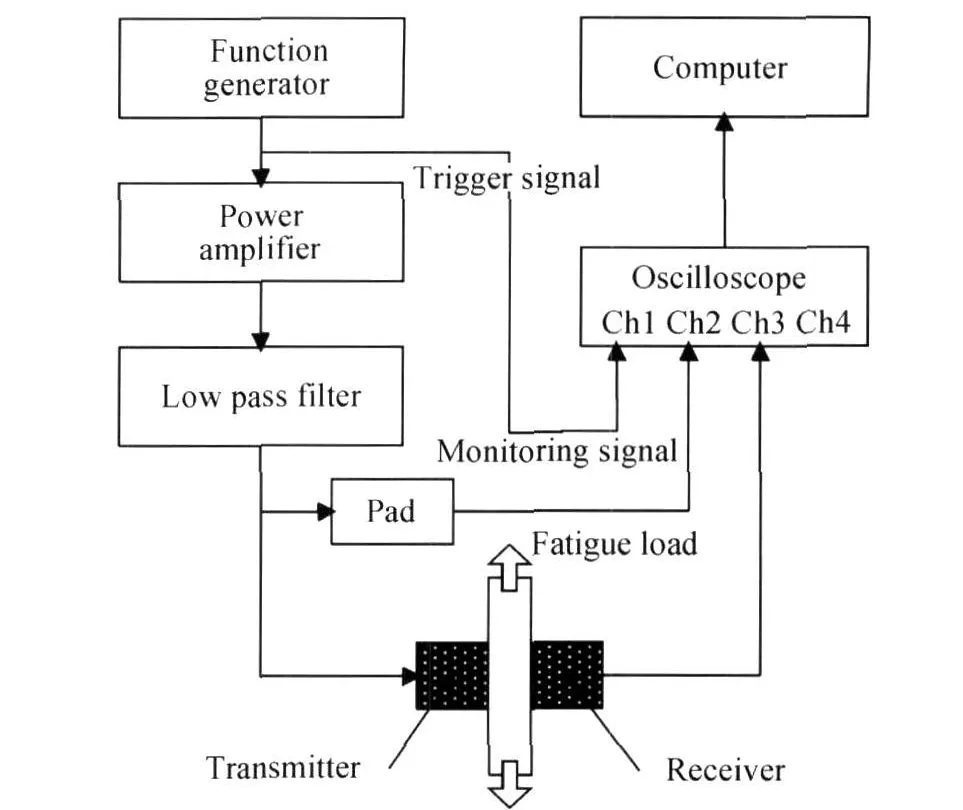
图1 实验系统示意图Fig.1 The layoutof experimental system

整个实验系统采用透射法测量基波和二次谐波的幅值。信号发生器产生的单频正弦波经放大、滤波后,驱动固定于被测试件一端的压电传感器,向试件中输入单频超声波。位于试件另一端的压电传感器将采集传来的包含有高频成分的超声波信号,然后对采集到的信号进行FFT变换,最终得到基波和二次谐波的幅值,进而确定非线性系数的值。

采用美国RETIC公司的高能低通滤波器来滤除功率放大器射频门产生的高频干扰。衰减器把从滤波器引出的一路信号衰减后作为监测信号输入示波器,通过监测信号可以控制输入发射传感器信号的幅值。一对中心频率分别为5MHz和10MHz的Panametrics窄带PZT超声探头作为发射和接收传感器。由于进行非线性测量时,激励信号幅值较大,普通耦合剂容易挥发,采用比较稳定的锂基黄油作为耦合剂。一个特殊的夹具来保证检测时探头和试件之间的充分和稳定的耦合,同时保持发射传感器和接收传感器在同一轴线上,以免能量损失。

图2为试件尺寸示意图,板厚7.5mm,材料为AZ31镁合金。半径为 157mm的圆弧中心处作为疲劳实验时的预设应力集中区域。试件表面均经过仔细的打磨抛光。共两组试件,第一组共一个试件用于拉伸实验,第二组共三个试件用于疲劳实验。

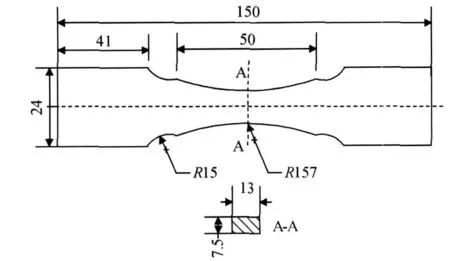
图2 试件尺寸示意图(尺寸/mm)Fig.2 Dimensions of specimen(mm)

为了减少仪器和随机因素产生的谐波干扰,取试件在厚度方向所能容纳的不与接收信号重叠的最大周期数作为正弦脉冲串信号周期数。根据超声波传播的距离和波速,确定本实验激励信号周期数为7。图 3a为接收时域信号,对接收到的时域信号进行FFT变换,在频率为5MHz的基频位置上可以得到基波幅值A1,如图3b实线所示;在10MHz的二倍频位置上可以得到二次谐波幅值 A2,如图3b虚线所示。

3 实验结果与分析

3.1 二次谐波幅值与基波幅值平方的关系

首先利用上述实验方法和装置对同一试件测量其在不同输入电压时的基波和二次谐波幅值,信号源电压取值范围为220mV到 320mV之间,间隔10mV。对测量到的实验数据进行线性拟合,得到图4所示测量 1的二次谐波幅值和基频波幅值平方的关系曲线,最佳拟合曲线方程为：

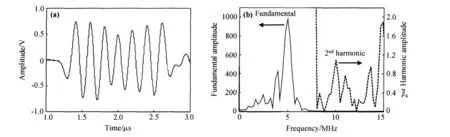
图3 基波和二次谐波幅值 (a)接收时域信;(b)基波和二次谐波幅值Fig.3 Amplitude of the fundamental wave and the second-harmonic wave (a)Received time domain signals; (b)Fundamentaland 2nd harmonic amplitude

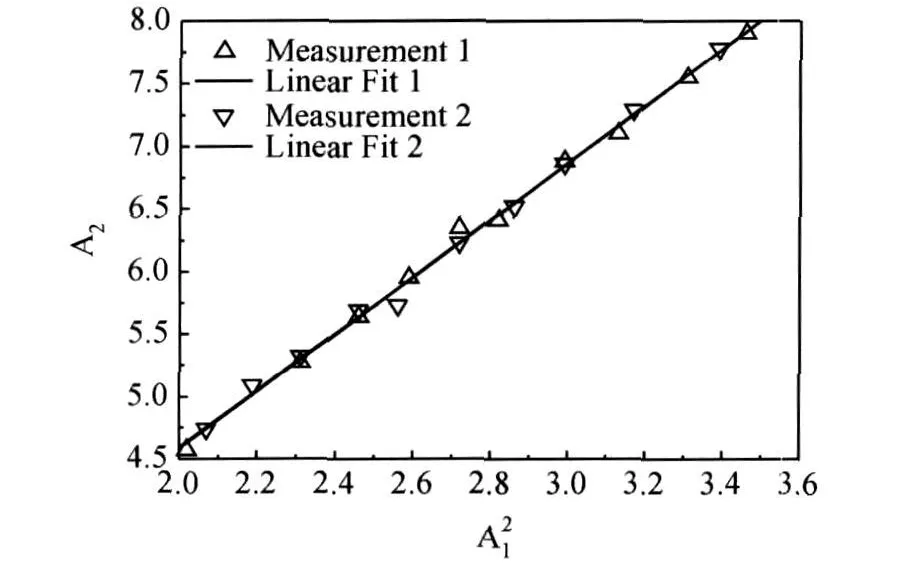
图4 二次谐波幅值与基波幅值平方的关系Fig.4 Second-harmonic amplitude versus the amp litude of the fundamental squared

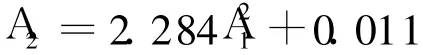
线性相关系数r=0.9986。

然后将传感器从试件拆除,完全清理耦合剂后重新安装,进行第二次测量。得到图 4所示测量 2的二次谐波幅值和基频波幅值平方的关系曲线,最佳拟合曲线方程为：

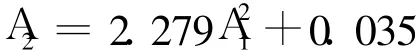
线性相关系数r=0.9984。

3.2 准静态拉伸实验结果

利用夹具把试件安装在MTS810全自动材料疲劳实验机上进行准静态拉伸实验。首先测量未拉伸试件的非线性系数 β0,然后拉伸到不同的应力时停止加载,测量试件的非线性系数 β,用 β/β0对超声非线性系数进行归一化,同时测量其应变。

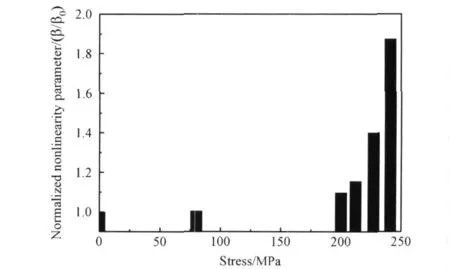
图5 归一化后的非线性系数与拉伸应力的关系Fig.5 Normalized nonlinearity parameter versus stress level

表1 拉伸试件的应力和应变Table 1 Stress and Strain ofmonotonic tensions specimen

图5为归一化后的超声非线性系数与拉伸应力之间的关系。可以分为两个阶段,在屈服前的弹性阶段,超声非线性系数没有明显的增长变化;在塑性阶段,随着拉伸应力的增大,超声非线性系数近似单调增加。表 1为试件的应力与应变对应关系。

3.3 拉伸试件原位微观观察

为了在微观结构上对实验结果进行验证,采用原位微观观察法对试样表面的位错滑移进行观察。观测仪器为KEYENCE VH-2500数字显微镜。试样如图 6所示。首先对试样的应力集中区表面进行打磨、抛光、腐蚀,在光学显微镜下观察试样的原始形貌。然后将试样在MTS810全自动材料疲劳实验机上施加单调拉伸应力。在不同应力阶段,对试样的同一位置进行微观观察。

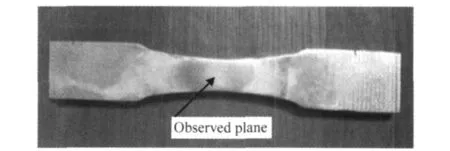
图6 微观观察试样Fig.6 The specimen ofopticalmicrostructures

实验所用腐蚀液为硝酸(1%)、草酸(0.5%)、乙酸(0.5%)和水(98%)混合溶液,腐蚀时间15s。在对试样拉伸加载的过程中,利用脱脂棉覆盖试样以保证观察面的清洁。

图7给出了拉伸试样在不同应力阶段下的光学显微图。从图中可以看出在原始和弹性阶段微观结构基本没有变化。进入塑性阶段后,应力为 200MPa时,沿晶界的位错滑移增多;应力为227MPa时位错滑移大量出现,晶界发生明显变形。

图7 不同应力阶段下拉伸试件的光学显微图Fig.7 Opticalm icrostructures ofmonotonic tensions specimen under different loading stress (a)Original;(b)80MPa;(c)200MPa;(d)227MPa

金属材料的塑性变形主要是通过位错运动实现的。根据文献[7],金属材料的非线性源于晶格的非谐和以及在施加一定外载荷情况下晶体内部出现的位错和滑移带等微观缺陷。在弹性阶段,金属材料内部微结构还没有发生明显变化,所以只存在由晶格的非谐和造成的金属材料固有非线性产生的谐波。进入塑性变形阶段后晶体内部位错密度和位错滑移等微观缺陷产生,非线性系数也会随之增大。因此,该实验结果是合理的。

宏观力学(应力、应变)、非线性超声检测和微观观察实验结果表明材料的超声非线性系数、应力应变和内部微观结构存在一定的关系。非线性系数β作为宏观和微观的桥梁可以表征材料的力学性能退化情况。

3.4 疲劳实验结果

疲劳试件共有A,B和C三个。A和B分别在MTS810全自动材料疲劳实验机上进行拉压疲劳,疲劳加载频率10Hz,R=σmin/σmax=-1。为了观察不同疲劳周数对实验结果的影响,给A试件较大的加载应力,取屈服极限的±65%(±129MPa),A试件的疲劳寿命为66500周;给B试件加载应力取屈服极限的±60%(±119MPa),B试件的疲劳寿命为113200周。C试件在疲劳实验机上进行拉 -拉疲劳,疲劳加载频率10Hz,R=σmin/σmax=0.1,加载应力为18.9 MPa-189MPa,C试件的疲劳寿命为43600周。因为材料疲劳本身的分散性和试件的个体差异,相同的试件在相同的实验条件下疲劳寿命并不一定相同。

首先测量未疲劳试件的非线性系数 β0,然后每隔固定周数停止疲劳加载,测量试件的非线性系数β,用 β/β0对超声非线性系数进行归一化。用疲劳寿命的百分数即试件不同循环加载周次与疲劳寿命的比值来表示疲劳损伤的程度。

图8给出了A,B和C试件归一化后的非线性系数与疲劳寿命的关系曲线。从图中可以看出,随着疲劳周数的增加,归一化后的相对非线性系数整体呈增长趋势,特别是疲劳早期近似于单调增加。虽然每个试件的实验结果存在一定差异,但曲线整体变化趋势相似,说明该组曲线可以表征材料疲劳早期退化的某种规律。每条曲线都可以分为两个阶段,第一阶段在疲劳寿命的 55%左右之前,超声非线性系数随疲劳周数的增加明显单调增加。第二阶段在疲劳寿命的 55%左右之后,非线性系数开始减小并出现较大波动。

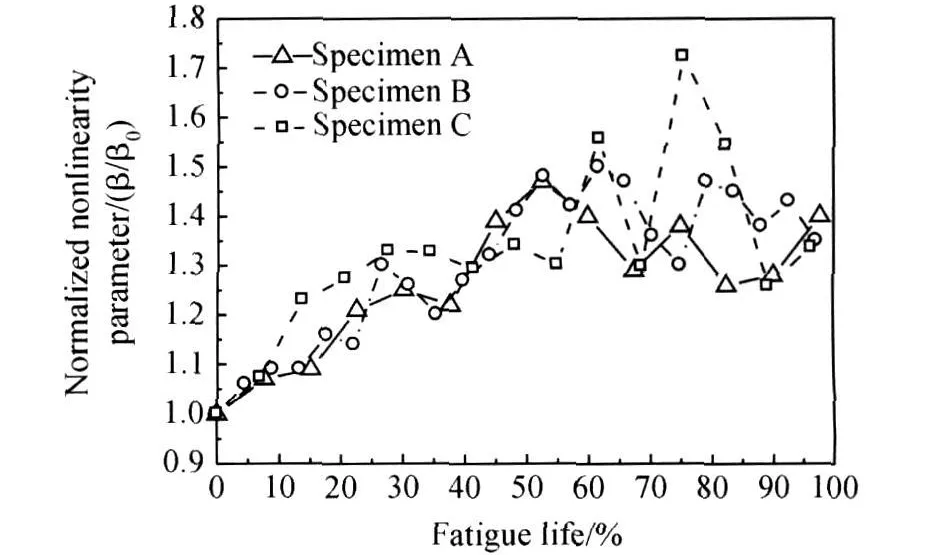
图8 A,B和C试件非线性系数与疲劳寿命的关系Fig.8 Normalized non linearity parameter versus fatigue life

在疲劳寿命的早期阶段,随着疲劳周数的增加,位错弦长、位错偶间距和位错密度增大,晶带滑移出现和增多,非线性系数也逐渐增大,当微裂纹开始萌生时非线性系数达到峰值。从实验结果看,与文献[9]的实验结果在数值和趋势上基本一致,说明非线性超声方法同样适用于AZ31镁合金。然后在疲劳寿命的晚期,位错密度趋于饱和,大量微裂纹开始出现,裂纹的存在使材料的衰减系数增大。而且超声衰减系数与频率的平方成正比,使二次谐波幅度衰减大于基波幅度衰减,非线性系数有所下降。另外,在疲劳寿命的后期,试件变形造成探头和试件之间耦合质量的下降,裂纹的开闭等因素也会使非线性系数的值减小和出现较大波动。

实验结果表明,金属材料超声非线性系数与疲劳寿命之间的关系可以用来表征材料的疲劳过程,如果事先对某种零部件的超声非线性系数曲线进行标定,则有望利用非线性超声无损检测技术来预测在役零部件的疲劳寿命。

A,B和 C试件的实验结果没有明显的规律性区别,说明在低周疲劳范围内,加载应力的大小以及拉-拉和拉-压疲劳模式的变化对实验结果没有明显的影响。

另外注意到,金属材料疲劳实验结果相比于拉伸实验结果虽然整体增长趋势相同,但具有更大的分散性,特别是在疲劳后期。这主要有两个原因, (1)实际实验时金属材料疲劳本身具有一定的分散性;(2)在疲劳寿命的后期材料内部会有大量疲劳裂纹出现,而疲劳裂纹的开闭使材料的非线性出现分散。

4 结论

研究发展了一套利用PZT压电传感器测量超声非线性系数的实验系统。利用该系统测量了AZ31镁合金拉伸和疲劳试件的超声非线性系数,实验结果表明,超声非线性系数对材料早期力学性能退化非常敏感。宏观力学、非线性超声检测和微观观察实验结果表明非线性系数 β作为宏观和微观的桥梁可以表征材料的力学性能退化情况。

[1]税国双,汪越胜,JIANMIN QU,et al.利用直接激发Rayleigh表面波的方法测量材料的声学非线性系数[J].声学学报,2008,33(4)：378-384.

[2]CANTRELL J H.Substructural organization,dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals[J].Proc R Soc Lond A,2004：316-322.

[3]SZILARD J.Ultrasonic testing：non-conventional testing techniques[J].John Wiley＆Sons Ltd,1982.

[4]NAGY P B.Fatigue damage assessment by non linearu ltrasonic materials characterization[J].Ultrasonics,1998, 36：375-381.

[5]JORDAN PM.Finite amp litude acoustic traveling waves in a fluid that saturates a porous medium：Acceleration wave formation[J].Physics Letters A,2006,355(3)：216-221.

[6]JHANG Kyung-Young.Nonlinear ultrasonic techniques for nondestructive assessment ofmicro damage in material：a review.International journal of precision engineering and manufacturing,2009,10(1)：123-135.

[7]CANTRELL JH,YOSTW T.Nonlinear ultrasonic characterization of fatigue microstructures[J].Int.J.Fatigue, 2001,23：S487-S490

[8]BUCK O,ALERSG A.New techniques for detection and monitoring of fatigue damage[J].Fatigue andmicrostructure.American Society for Metals,1979：101-147.

[9]KIM JY,JACOBSL J,QU J,etal.Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves[J].Journal of the Acoustic Society of America,2006,120(3)：1266-1273.

[10]SHUIGuoshuang,KIM Jim-Yeon,QU Jianmin,et al.A-new technique for measuring the acoustic nonlinearity of materials using Rayleigh waves[J].NDT＆E International 2008,41(1)：326-329.

[11]徐从元,姜文华.疲劳金属材料非线性声学特性的试验研究[J].南京大学学报,2000,36(3)：328-335.

[12]税国双,汪越胜,曲建民.材料力学性能退化的超声无损检测与评价[J].力学进展,2005,35(1)：52-68.

[13]SOHN K Y,JONESJW,BERKMORTEL J,et al.Creep and Bolt Load Retention Behavior of Die Cast Magnesium Alloys for High Temperature App lication[C].SAE Technical Paper Series,20002-012-1120,Warrendale, PA,2000.

[14]胡艳辉,李建国,谭敦强,等.细晶 AZ31镁合金高温压缩变形行为研究[J].航空材料学报 ,2010,30(1)：36 -40.

[15]BREAZEALE M A,PHILIP Jacob.Determ ination of Third order Elastic Constants from Ultrasonic Harmonic Generation Measurements[C].Physical Acoustics,Vol. 17,Academ ic Press,INC.1984.

[16]CANTRELL J H.Crystalline structure and symmetry dependence of acoustic nonlinearity parameters[J].JApp l Phys,1994,76(6)：3372-3380.

[17]Hurley D C,Fortunko C M.Determination of the non linear ultrasonic parameterβusing a Michelson interferometer [J].Meas Sci Technol,1997,8：634-642.

[18]YOST W T,CANTRELL JH.Materials characterization using acoustic nonlinearity parameters and harmonic generation.Rev.QNDE,1990;9B：1669-1676