基于计算机编程技术的数学近似计算研究

王卫生，刘 颖，郭 亮

(1.哈尔滨工业大学城市水资源与水环境国家重点实验室，哈尔滨150090; 2.辽宁信息职业技术学院软件工程系辽宁辽阳111000)

随着计算机技术的飞速发展和广泛应用，计算机运算速度快、存储信息量大、并且有逻辑判断能力等特点突显出来，成为人们解决纷繁复杂问题的有效工具，很多实用的数学软件也应运而生.通过选择近似计算的几个典型实例，编写相应的程序设计内核语句来求解实用问题是至关重要的.基于计算机编程技术，本文对一些数学的近似计算进行了研究.

1 在求无理数近似值方面的研究

在高等数学中，一提到近似计算的问题时人们自然会联想到泰勒公式［1］:对于函数f(x)在x0的某邻域内n+l阶可微，则在此邻域内有式(1)成立.

这里Rn(x)的称为拉格朗日余项，该余项值的大小决定了函数f(x)计算的精度.通常为达到一定的精度时需要求解关于Rn(x)的不等式来确定n的范围，从Rn(x)的不等式可以看出求解这个不等式的难度.然而在程序设计中我们只要在循环语句中对循环条件加以限制就可以轻松地达到目的.

下面以求无理数e的近似值为例，通过程序设计完成e的近似值的计算.由公式(1)很容易推导出ex的计算公式:

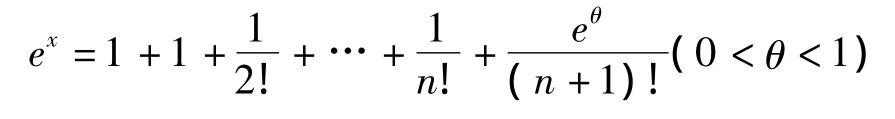
当x=1时就是求解无理数［0，1］的公式:

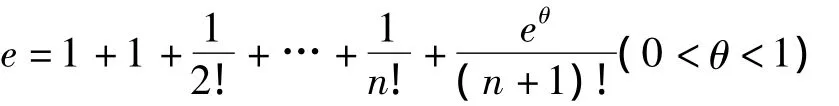
求解过程中当精度被确定时(比如误差不超过)我们很难通过求解不等式的来确定满足条件的n的最小值，而借助程序设计中的循环语句中的循环条件的设定将轻松地解决该问题.程序如下:

运行结果如下:

通过运行程序可以看出:把原本很复杂的求不等式来确定满足条件的最小值n的问题转化为“把所需精度作为循环的条件进行设置”，省去了很多因计算带来的烦恼.而效率却大有提高.

2 在求解方程近似根方面的研究

在科学研究与工程技术中，常会遇到求解非线性方程f(x)=0的根的问题.我们知道对于不高4次的代数方程已有求根公式，而高于4次的代数方程则无精确的求根公式，至于一般的超越方程就更无法求其精确解了.因此，如何求得满足一定精度要求的方程的近似根也就成为了广大科技工作者迫切需要解决的问题.解决此类问题的方法很多包括:二分法、迭代法、牛顿切线法、弦截法［2－3］等.我们下面用较好理解的二分法来求方程y=x3－x－1在区间内根的近似解，精确度要求:E=0.000 001.函数图像如图1所示

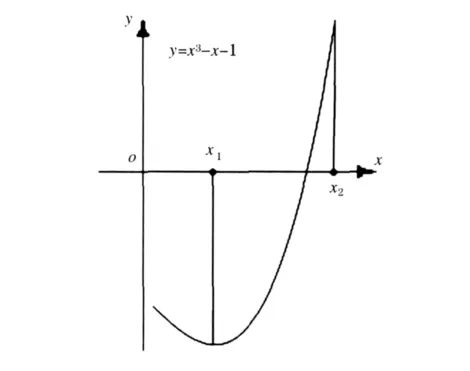
图1 函数y=x3－x－1的图像

原理:若函数f(x)在区间［x1，x2］两端点的函数值异号，则在区间［x1，x2］内方程f(x)=0至少有一个根.如果在区间［x1，x2］内f(x)仅有一个根x，则可以取x与x的中点进行判断，12若f(x3)与f(x1)异号，说明有一个根在区间［x1，x3］中，否则在区间［x2，x3］中.然后按上述二分方法逐渐缩小有根区间，从而逼近方程f(x)=0的根.当有根区间小到一定程度时，把这个区间的中点的X值当作方程的近似根.

根据该原理编写程序如下:

运行结果如下:

在范围1.00E～10E－1内变换不同的精度，列出精度与根的对应表，如表1所示.

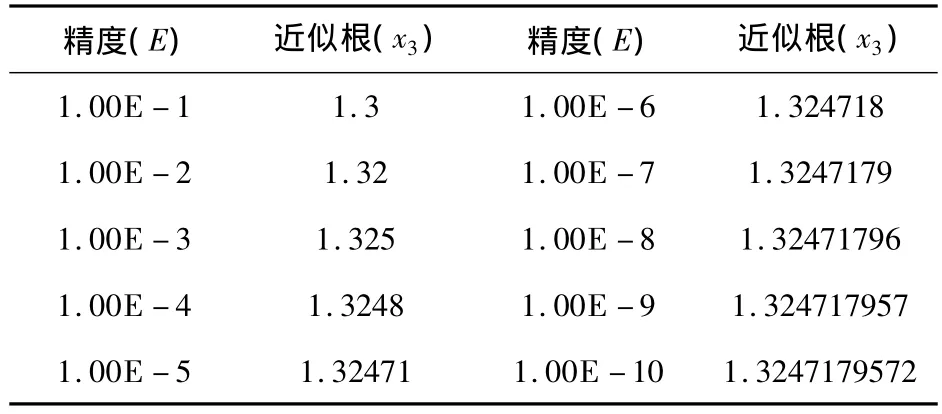
表1 精度与根的对应表

本文利用SPSS分析软件［4］对近似根(x3)和精度(E)的变化绘画出图像如图2所示.

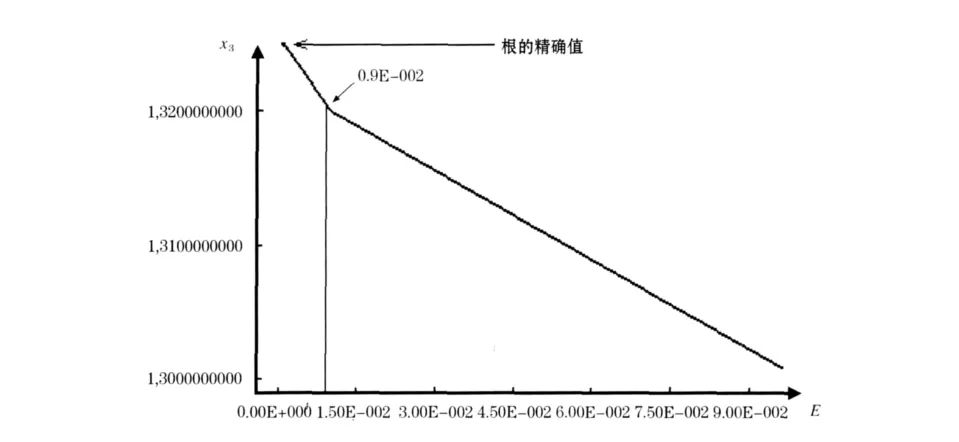
图2 近似根和精度的关系图

通过图像可清晰地看到:当精度在［0.9E－002，9.00E－002］范围变化时(值越小精度越过)，近似根以线性方式快速逼近方程的根;当精度值在(0，0.9E－002)范围变化时，近似根仍以线性的方式、更高的速率逼近方程的根，同时在此区间的方程的近似根和根的精确值接近程度已经很高了.

3 在求解不规则图形面积方面的研究

原理:把对应区间分成n等份，将出现n个等底的矩形，我们用这n个矩形的面积的和来近似地表示不规则图形的面积.可以通过调整n的大小来体现近似值与真值的逼近程度.

图3 函数f(x)在区间［0，1］上被分割后的图像

编写程序如下:

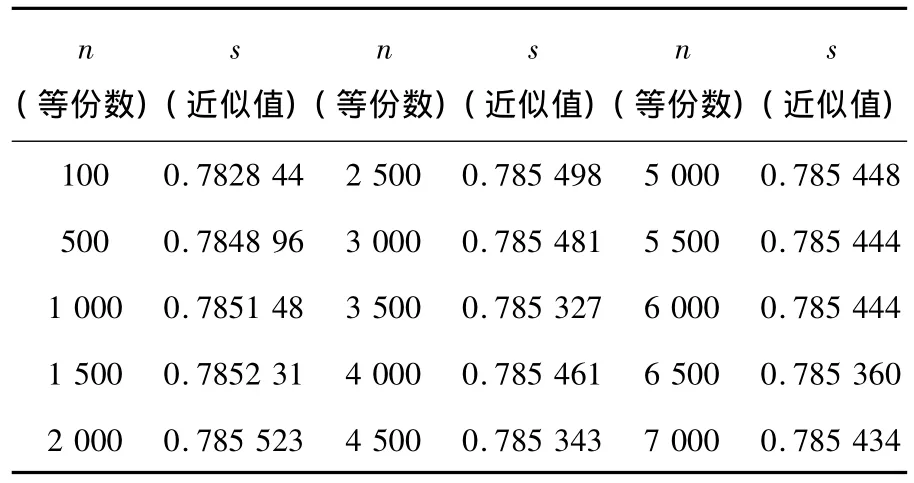
表格2 近似值与等份数关系表

利用SPSS分析软件对等份数和近似根的变化绘画出图像，如图4所示.

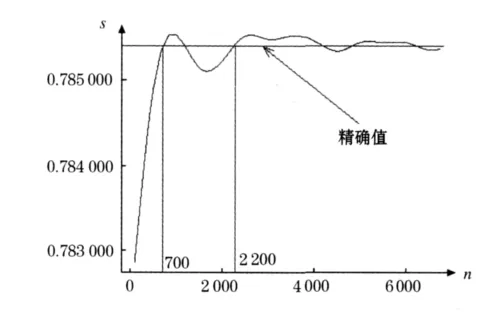
图4 近似根与等份数的关系图

通过观察图像可以得到以下结论:

1)当0＜n＜700时，近似值随着等份数的增加逐步逼近图形的精确值(通过定积分求出).

2)当700＜n＜2 200时，近似值随着等份数的增加，近似值将围绕精确值有较大幅度地波动.

3)当n＞2 200时，近似值将围绕精确值有小幅度地波动，并随等份数的增大波动幅度就越小.

4 结语

运用计算机程序设计方法解决数学问题，无论在数学界还是在计算机应用领域都有广泛的发展空间，在不久的将来，许多涉及计算、图形、文字处理的功能强大、界面友好的汉语软件将被开发出来，许多业内人士将从繁琐的计算和批量的作图中摆脱出来，极大提高生产效率.

［1］ 朱永生，刘莉.基于泰勒公式应用的几个问题［J］.长春:长春师范学院学报:自然科学版，2006.

［2］ 谭浩强.C语言程序设计［M］北京:清华大学出版社，2008:55－60.

［3］ 钱 能.C++程序设计［M］.北京:清华大学出版社，2004年，55－57.

［4］ 张红兵，贾来喜，李 潞.SPSS宝典［M］.北京:电子工业出版社，2007:117－119.

［5］ 刘习贤，华柳斌.高等数学［M］.上海:同济大学出版社，2009:223－225.