群时延内均衡的模拟滤波器优化设计

李 鹏,马红梅

(华北科技学院,北京 101601)

1 引 言

群时延是滤波器最重要的性能指标之一,反映相位随频率变化的快慢,其理想状态为一条水平直线,其值应该是一个常数。在信号的传输过程中,如果群时延波动过大,会使信号产生畸变,对数字信号而言,因为相邻码元之间不同频率分量通过群时延滤波器之后的时延不同,导致接收方接收到的信号会在相邻码元之间产生串扰,增加误码率[1]。用网络综合法设计的滤波器的群时延波动非常大,如何取得滤波器理想的带外衰减和较小的带内群时延,常常是滤波器设计的难点[2]。一般的解决办法是用时延均衡器来均衡。普通滤波器的群时延特性犹如锅底状,如果外加均衡器来“补平”则叫做外均衡,在滤波器内部采用特殊措施实现群时延均衡的称为内均衡。无论是内均衡还是外均衡,虽然能够使群时延波动相对变小,但是时延均衡器的参数是固定的,只能被动地相对减小群时延波动,而不能从根本上解决带内群时延波动过大的问题。另外,加入均衡都会增加整个滤波器的元件数量,以致增大体积,加大损耗,增加成本[3]。

随着现代高质量通信系统的发展,不仅要求滤波器幅频响应满足特定的指标,同时还要求在通带内具有较小的群时延特性。而相频特性和幅频特性之间又存在着矛盾,为使滤波器的幅频特性和群时延特性在合理折衷的条件下各自达到最佳状态,本文提出了一种群时延内均衡的滤波器优化设计方法。首先根据设计指标先对滤波器的幅频特性进行优化,然后内接时延均衡器,在通带内用最小二乘法拟合一条水平直线作为理想曲线的初值,然后优化元件参数,使群时延特性曲线向这条直线逼近,同时优化整个滤波器的幅频特性。重复上面的过程,直到获得最佳的元件参数为止[4]。

本文中实例的幅频特性的设计已经发表在文献[4]中,在网络综合法设计的滤波器基础上,利用作者提出的极点放置技术和优化技术先使滤波器的幅频特性算术对称[1],再内接二阶时延均衡器,最后同时优化幅频特性和群时延特性,降低群时延的波动。

2 时延均衡器直接耦合

利用文献[4]提出的极点放置技术和优化技术设计出来的滤波器虽然幅频特性能达到算术对称,但相频特性很难接近线性,为解决此问题,需要在电路中加时延均衡器。一阶均衡器仅有一个设计参数,对群时延的均衡效果有限,所以一般都选用二阶均衡器。二阶均衡器有两个设计参数 Wr和Q,Wr是群时延最小值处的频率,Q是滤波器的品质因数。通常要根据Wr和Q来计算二阶均衡器的各个元件参数。本文采用内均衡方式直接耦合时延均衡器[5]。

3 幅频和群时延特性模型的建立

3.1 滤波器幅频特性目标函数的建立

滤波器幅频特性的数学模型在文献[4]中已经给出 ,即:

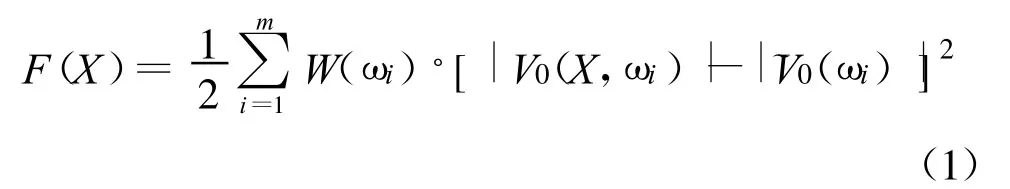
3.2 群时延特性目标函数的建立

建立滤波器群时延特性数学模型,先在通带内取p个频率点,然后求各个频率点群时延的实际值与理想值之差的平方和,目标函数可以写成:

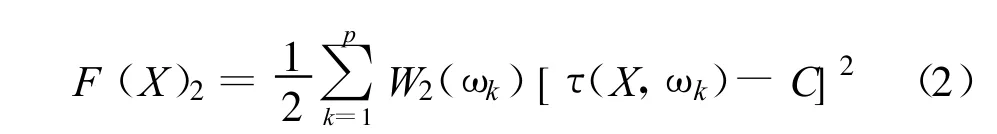
式中,W2(ωk)为各频率点 ω′1,ω′2,ω′k,…,ω′p上相频特性的权重函数;τ(X,ωk)为各个频率点上实际的群时延值,其值可由相位求导得到;C为理想的群时延特性曲线,其值为一常数。

3.3 滤波器总目标函数的建立

滤波器总的目标函数就是幅频特性目标函数与群时延特性目标函数之和,即:

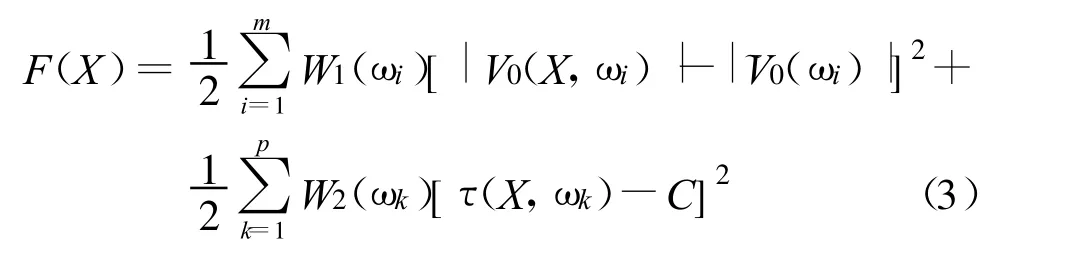
4 滤波器的优化

4.1 目标函数的梯度

对目标函数进行优化,首先要求出目标函数的梯度。幅频目标函数的梯度在文献[4]中已经给出,对群时延特性的梯度,因为群时延是相位对频率的一阶导数,为使编程方便,所以把群时延的梯度转换为对相位的梯度,即:

式中,τp为相位延迟,φ为相位,ω为角频率。转换后的梯度为

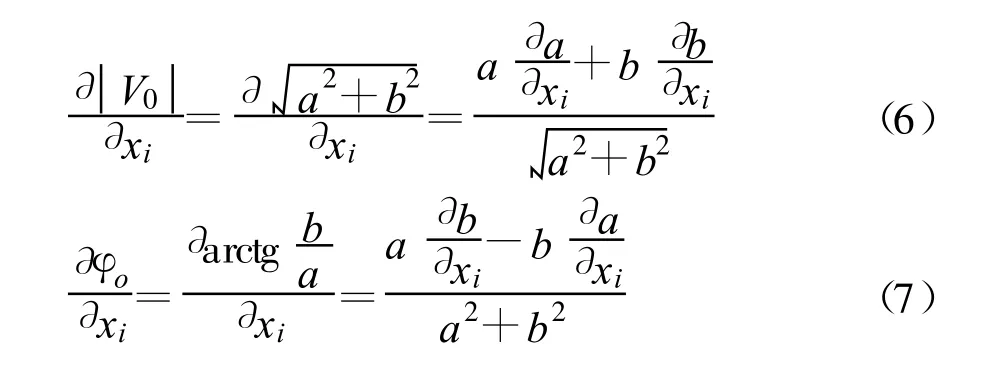
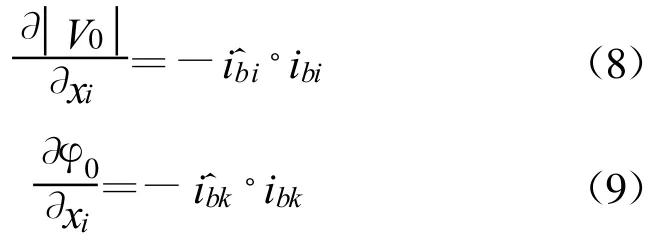
4.2 优化过程

对于群时延特性,需要将目标函数向一个常数优化,这个常数可以由最小二乘法求得。对总的目标函数,利用无约束最优化方法可以使目标最小,此时幅频特性接近于理想状态,群时延接近于常数。

5 实例分析

以设计一个无源带通滤波器为例,中心频率是490MHz,3 dB带宽为70MHz,线性坐标下±90MHz处衰减大于55 dB,矩形系数小于2.5,群时延波动小于12 ns,两端接电阻都是50Ψ。

6 网络综合法设计

6.1 幅频特性设计

对滤波器幅频特性的设计,采用六阶电容耦合谐振滤波器,具体电路和参数以及幅频特性在文献[4]中已经给出。图1为通带内的群时延特性曲线。

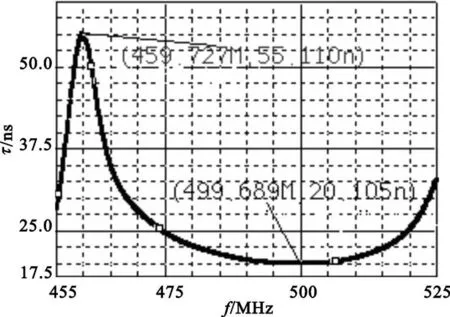
图1 滤波器的群时延特性Fig.1 Group-delay of the filter

6.2 时延均衡器直接耦合

从图1可以得出,通带内群时延波动的最大值是35.05 ns,在峰值处的频率为499.69 MHz,再根据二阶时延均衡器的设计公式可以得出Q的大概值为[5]27.51。耦合时延均衡器后的电路如图2所示。

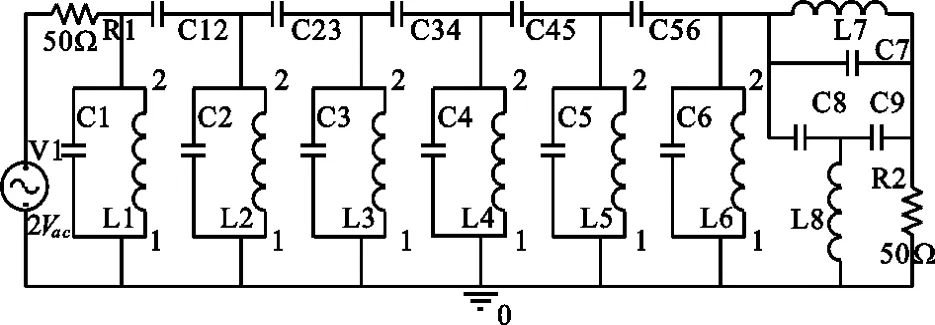
图2 时延均衡器直接耦合电路Fig.2 Filter circuit coupledwith group-delay equalizer

时延均衡器直接耦合后,幅频特性基本保持不变,群时延特性如图3所示。

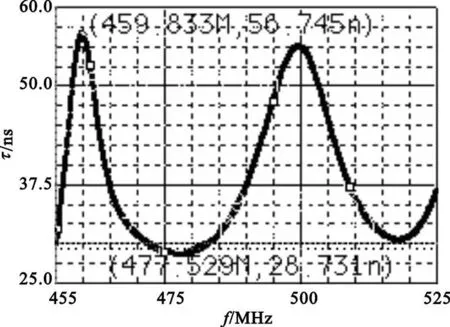
图3 时延均衡器直接耦合后的群时延特性Fig.3 Group-delay of the filter coupled with group-delay equalizer

由仿真可以得出,在490±35 MHz处的衰减分别为10.968 dB和0.2647 dB,在 490±90MHz处的衰减分别为76.383 dB和47.698 dB,通带内群时延的最大波动为28.014 ns,此时滤波器的通带偏向高频处且不算术对称。

7 优化设计

7.1 幅频特性的优化

优化法设计时延滤波器,首先利用极点放置技术对电路进行改进,然后再对滤波器的幅频进行优化。改进后的电路及优化后的幅频特性参见文献[4]中的图4和图5,群时延特性如图4所示。

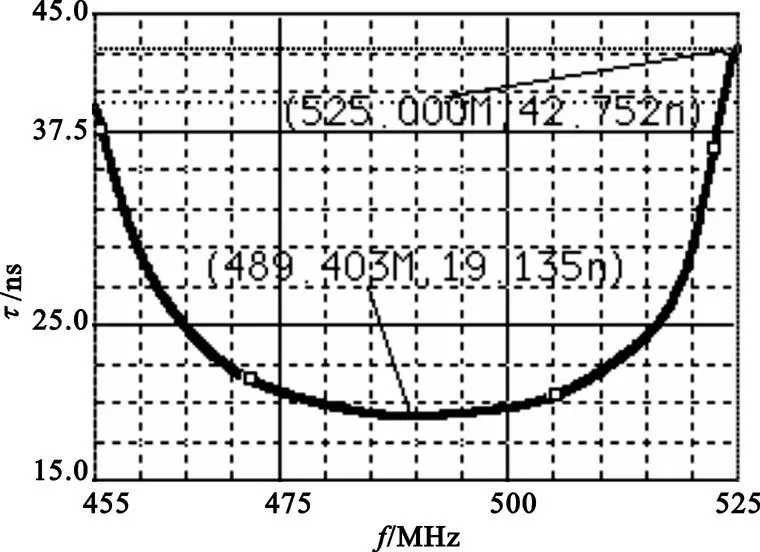
图4 幅频优化后的群时延特性Fig.4 Group-delay of the filter′s amplitude-frequency optimized

7.2 时延均衡器直接耦合

从图4可以看出,通带内群时延波动的最大值是23.617 ns,在峰值处的频率为489.403MHz,再根据二阶时延均衡器的设计公式可以得出 Q的大概值为18.156[5]。耦合时延均衡器后的电路和群时延特性如图5和图6所示,此时滤波器的幅频特性基本不变,通带内群时延波动的最大值减小到16.584 ns。

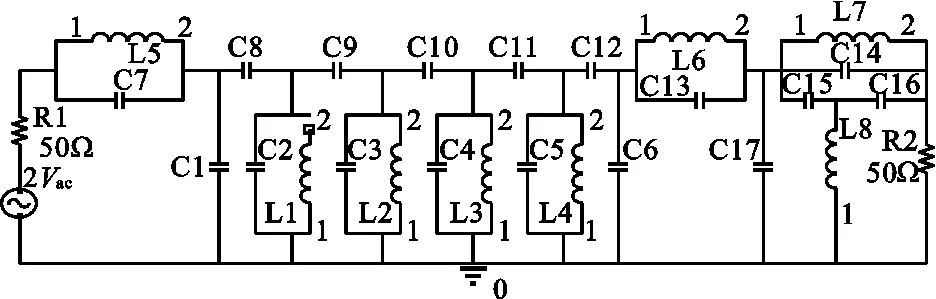
图5 改进的时延均衡器直接耦合电路Fig.5 Improved filter circuit coupledwith group-delay equalizer

图6 时延均衡器直接耦合后的群时延特性Fig.6 The filter′s group-delay coupled with group-delay equalizer

7.3 电路整体优化

对整个电路的幅频特性和群时延特性同时进行优化,优化后的曲线分别如图7和图8所示。

图7 优化后的幅频特性Fig.7 Amplitude-frequency optimized

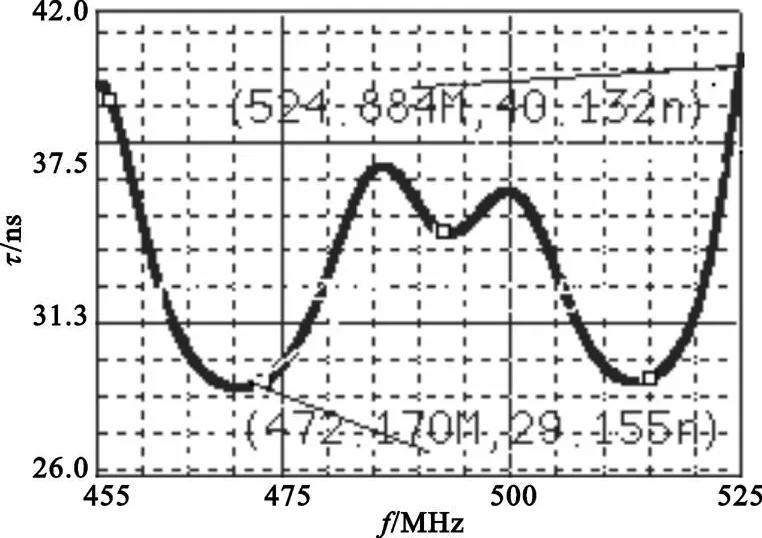
图8 优化后的群时延特性Fig.8 Group-delay optimized

由仿真可以得出,在490±35 MHz处的衰减分别为2.0492 dB和0.554 dB,在490±90MHz处的衰减分别为55.901 dB和60.355 dB,通带内群时延的最大波动为10.977 ns。

8 结 论

Pspice仿真结果表明,用网络综合法设计的内接时延均衡器的滤波器,其通带内群时延最大波动为28.014 ns,幅频特性在线性坐标下不对称;优化后的幅频特性基本上是算术对称的,通带内群时延最大波动为10.977 ns,只有网络综合设计法的39.18%。设计实例表明,优化设计方法相比于网络综合设计方法来说,不但能够使幅频特性和群时延特性达到合理的折衷,而且能够解决网络综合设计方法难以实现的线性群时延设计问题,具有良好的工程应用价值。

[1]王大寿,赵涛.LC滤波器的小型化制作与生产[J].大连海运学院学报,1994,20(4):60-66.WANG Da-shou,ZHAO Tao.The miniaturization make of the LC filters[J].Journal of Dalian Marine College,1994,20(4):60-66.(in Chinese)

[2]江山.窄带小群时延波动晶体滤波器设计[J].电讯技术,2010,50(3):54-58.JIANG Shan.Design of Narrow band Little Ripple Group delay Crystal Filter[J].Telecommunication Engineering,2010,50(3):54-58.(in Chinese)

[3]沙海.卫星导航系统传输信道的群时延测量方法研究与应用[D].长沙:国防科技大学,2009.SHA Hai.Research andApplication of the Group Delay Measurement Method in Transfer Channel of Satellite Navigation System[D].Changsha:National University of Defense Technology,2009.(in Chinese)

[4]李鹏,马红梅.幅频算术对称无源带通滤波器的优化设计[J].电讯技术,2010,50(6):105-108.LI Peng,MA Hong-mei.Optimization Design of Amplitude-frequency Arithmetic Symmetry Passive Bandpass Filter[J].Telecommunication Engineering,2010,50(6):105-108.(in Chinese)

[5]阿瑟·B·威廉斯.电子滤波器设计手册[M].北京:电子工业出版社,1986:201-208.Arthur B Williams.Design Handbook of Electric Filter[M].Beijing:Publishing House of Electronic Industry,1986:201-208.(in Chinese)