新型高效射频预失真器的分析与设计

宁高利,谢拥军,2,雷振亚

(1.西安电子科技大学天线与微波技术国家重点实验室,西安 710071;2.北京航空航天大学电磁兼容实验室,北京 100083)

1 引 言

功率放大器是无线通信系统中的一个基本组件。近年来,无线通信领域内的各种线性调制方式和多载波应用的出现对功率放大器的效率和线性度提出了越来越高的要求。为了获得较高的效率,功放通常工作在非线性区,然而此时也会呈现出非线性(即引起输出信号的失真),进而引起频谱再生,干扰邻道信号。为此,人们提出了各种线性化技术,如功率回退、前馈法、预失真法、负反馈法等[1—2]。其中模拟预失真法因能直接放大手持设备与基站之间的射频信号,可应用于直放系统而备受青睐[3—9]。预失真方法实质上是在功率放大器输入端引入了具有与之等值反相的幅度和相位失真的预失真信号,来抵消放大器自身产生的失真,最终获得无失真的输出信号。

传统的基于单个二极管或反向并联二极管对的预失真电路,仅通过调节二极管偏置来控制预失真特性,调节自由度受限[3]。有报道使用微控制器来控制不同参数以获得需要的预失真特性,这种方法很有效,但其电路复杂度明显增加,体积和成本增大[4]。一种更灵活的方案是直接通过混频器产生预失真分量,再经衰减器和移相器适当地衰减和移相后,加到放大器的输入端,以抵消功放自身的非线性失真效应[5],显然,它极大地增加了复杂度和成本,牺牲了效率。本文首先从功率放大器中非线性产生的根本原因入手,通过理论分析指出为了灵活有效地产生期望的预失真特性,预失真器应包含至少两个自由调节变量,这就为此类电路的设计提供了一定的理论依据。在此基础上提出的新型射频预失真器,不需要混频、衰减、移相、耦合这些组件,以及额外的直流偏置,仅使用了一个二极管和分别与之串联和并联的电阻和电容,从而使得线性度在得到有效改善的同时,电路复杂度大大降低。

2 功率放大器非线性的理论分析

众所周知,功率放大器经常工作在大信号状态,因而引起输出信号的失真,表现出非线性的传输特性。从根本上说,这种失真分为幅度-幅度(AMAM)和幅度-相位(AM-PM)失真。如图1所示,随着输入信号的增加,增益的幅度被压缩;另一方面,其相位也改变。为了定量分析这种现象,幂级数法因其简单明了和操作方便而被广泛使用,显然,这种方法只考虑了AM-AM失真。为了同时考虑到AM-AM和AM-PM失真,这里使用了广义幂级数法。所谓广义幂级数是指将时延引入到各项的系数中去,即此时的系数为复数。广义幂级数法适用于具有强非线性的功率放大器。

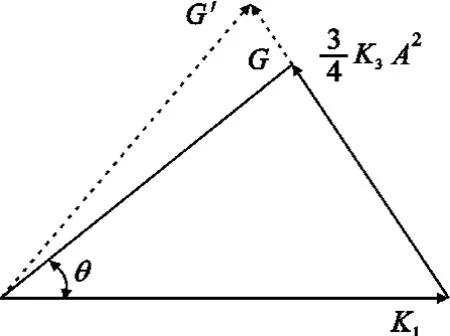
图1 功率放大器的“复增益”与其输入之间的关系Fig.1 “Complex gain” of PAs vs.input

我们使用广义幂级数法对功率放大器中的非线性失真进行分析,进而得出如何将其最小化。工作在非线性区的功率放大器的转移函数可以表示为

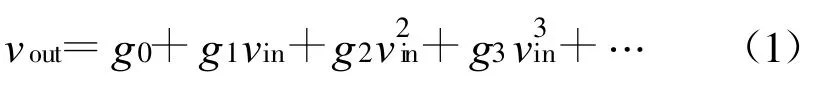
式中,vout是功率放大器的输出信号;vin是输入信号;gi(i=0,1,2,…)是各项系数,是具有幅度和相位的复数,其值与具体电路有关。这里,gi的幅度和相位分别用来代表AM-AM和AM-PM失真效应。假定输入为单音信号,vin=Acosωit,则式(1)可以写为

上式表明,由于其非线性,输出信号中不仅有原基频信号分量,还产生了新的直流分量和各次谐波分量。正是这些直流分量和各次谐波分量携带走了部分能量,从而降低了效率,引起了输出信号的非线性失真。若输入信号是双音信号,vin=Acosω1t+Acosω2t,将其代入式(1),则会得到如式(3)所示的大量频率分量产物:

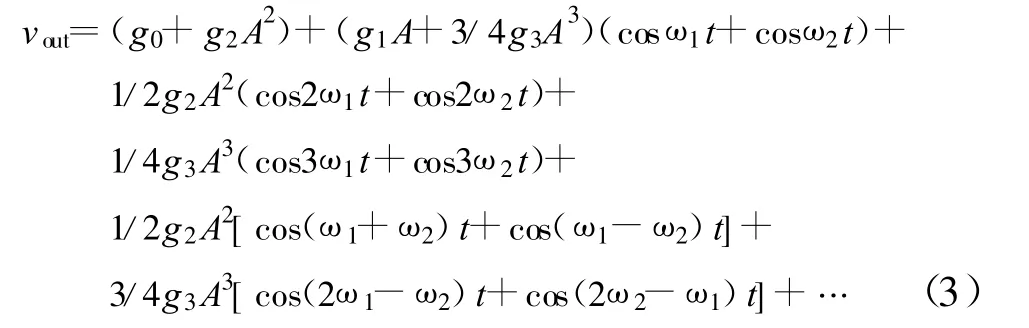
与单音输入情况相比,这时输出信号中又多了互调产物。一般情况下,随着阶数的增加,其系数迅速减小,因而高阶项可以忽略。由原偶数阶项产生的互调产物与输入信号频率间隔较远,因而也不会对带内失真产生较大影响(谐波情况与此相同)。因此,我们仅需要考虑由原奇数阶项引起的互调产物。其中,三阶互调产物cos(2ω2-ω1)t]影响最大,这是因为:它落在了信号频带内,并且与输入信号频率间隔很小,无法用滤波器将其滤除;与其它带内互调产物相比,其幅度远远大于其它分量。至此,我们看到三阶互调失真产物是功率放大器的主要非线性源,它对放大器的非线性特性影响最大。

由式(3)我们可以看出,三阶互调失真产物主要来源于功率放大器转移函数中的三阶项,因为它仅与系数g3有关。这意味着,为了使某个功率放大器线性化,我们只要最大程度减小其三阶项即可。在预失真技术里,预失真器级联在功放的前面。预失真器由于包含了二极管、场效应管等,属于非线性组件,故其转移函数可表示为

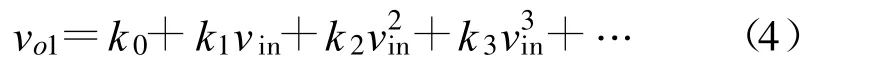
式中,vo1是预失真器的输出信号;vin是其输入信号;ki(i=0,1,2,…)是包含幅度和相位的复数,分别用以代表AM-AM和AM-PM失真效应,其值同样与具体的预失真电路有关。在此,我们重新写出功率放大器的转移函数如下:

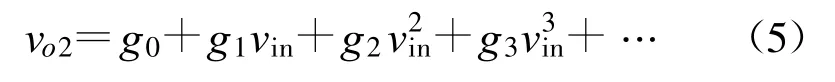
式中,各项与式(4)中的对应项有类似的含义。将式(4)代入式(5),得到由预失真器和功率放大器组成的整个部件的传输函数。通过展开、合并整理,得到其三阶项系数如下:

由上述分析我们知道,为了获得一个线性系统,应该让G3趋于零,进而得到:

为了抑制输出中的三阶非线性失真,预失真电路的系数应满足上述关系。预失真电路的特性可以通过k1和k3来调节。注意到式(7)是一个复数方程,为了保证其解总是存在的,预失真器应该具有至少两个独立变量,以使得其非线性的幅度和相位能得到灵活有效的控制。

到此,我们是直接从本质上去研究线性化问题的(即从非线性失真产物的角度),这可以从图2直观地得到解释。另外,我们还可以从基频信号的角度来考察。图3给出了对应于基频信号的“复增益”(G)与其输入信号(Pin)之间的关系。在功放中,随着输入信号的增加,非线性失真产物逐渐增大,它们带走了越来越多的能量,从而使得其“复增益”的幅值(Mag.)减小,称为“增益压缩”。同时,随着输入信号的增加,其相位(Phase)超前。图3(a)则给出了预失真器的理想性能,即增益扩张和相位滞后,与功放的恰好相反。从而,预失真器和功放两者结合起来则表现出线性特性,即“复增益”的幅度和相位均为常数,如图3(c)所示。

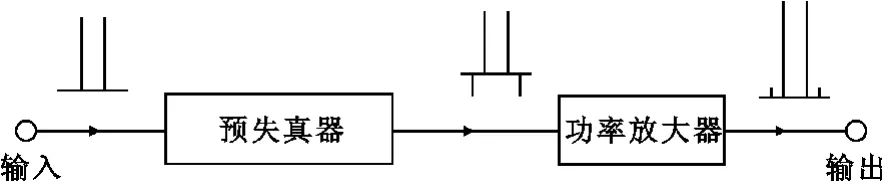
图2 线性化原理方框图Fig.2 Block diagram of the linearization principle

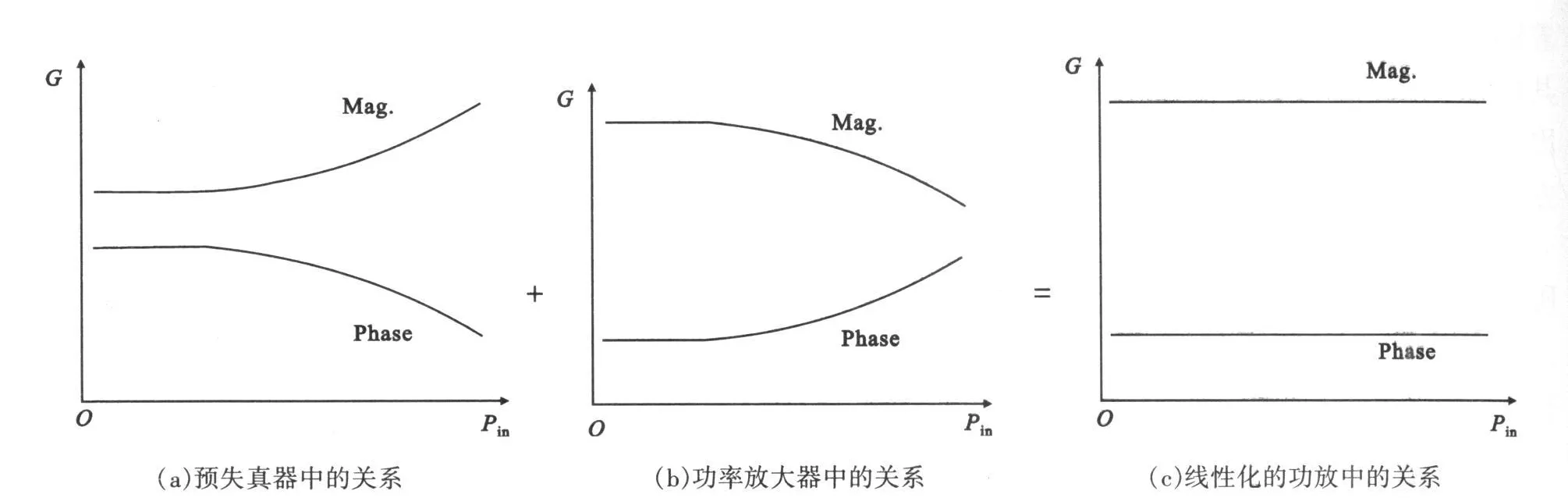
图3 “复增益”与其输入之间的关系Fig.3 Dependence of“complex gain” on input

3 预失真器电路分析

基于上文分析而得到的结论,在此提出了一个简单而有效的预失真器,如图4所示。它由一个二极管和分别与之串联和并联的电阻和电容组成,这里的电阻和电容充当着前面提到的两个独立的调节变量。根据给定功放的失真特性,可以通过调节电阻电容的值来获得期望的预失真特性。环行器接待线性化的功放(端口2),同时它也提高了输入口(端口1)的回波损耗特性。

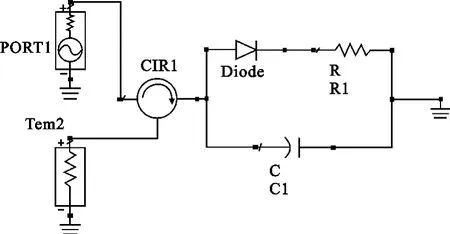
图4 预失真器的结构Fig.4 Configuration of the proposed predistorter

二极管所遵循的伏安关系为式中,iD是通过二极管的电流,vD是其两端电压,Is是其反向饱和电流,α是与其制造半导体工艺有关的一个参数。二极管给定时,Is和α就确定了。假定vD是单音信号:

iD则可展开成傅里叶级数:

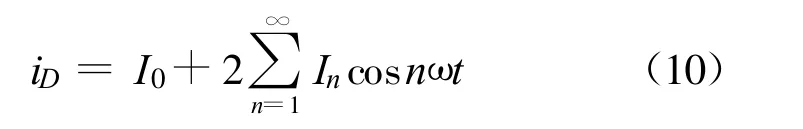
式中,In是傅里叶系数,并可写成:

相对于基频信号,二极管所呈现出的阻抗为

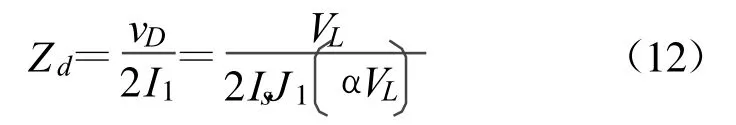
式中,Zd是二极管阻抗,J1(α VL)是第一类一阶贝塞尔函数。根据大宗量近似,当 α VL足够大时,可简化为

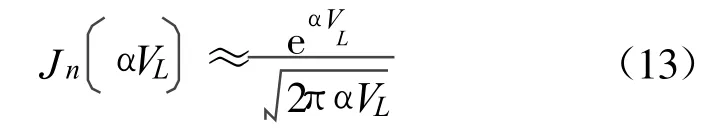
再通过简单的推导即可得到其反射系数为

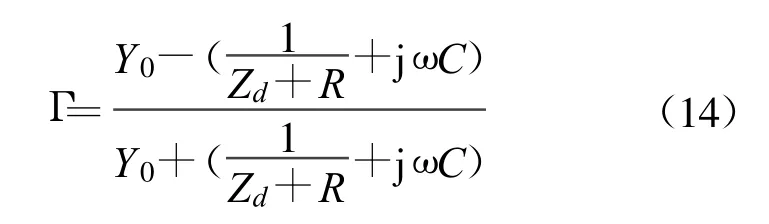
由于R和C是两个独立的可调节变量,所以能够灵活有效地控制预失真器的AM-AM和AM-PM特性,以产生期望的输出。

4 结果与讨论

为了进一步验证设计的预失真器,我们将其应用于功率放大器,考察它对线性度指标的实际改善情况。这里使用的功放可用于直放站或基站应用中,其工作频率为1.9 GHz,1 dB压缩点输出功率为43 dBm,其线性度和效率性能如图5和图6所示。

图5 非线性功放的三阶互调失真系数与其输出功率之间的关系Fig.5 Nonlinear PA′s IMD3 vs.its output power

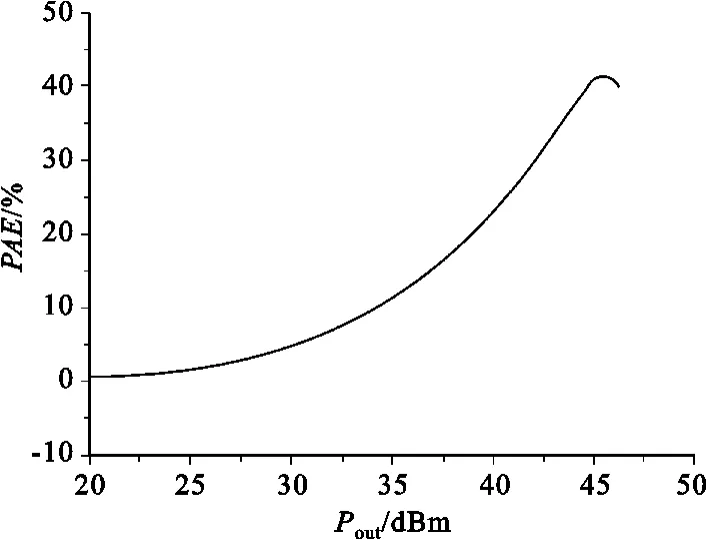
图6 非线性功放的功率附加效率与其输出功率之间的关系Fig.6 Nonlinear PA′s PAE vs.its output power

双音测试是一种评估放大器线性度的被普遍认可的方法,它能够同时说明存在于放大器中的幅度和相位失真。将中心频率为1.9GHz、频率间隔为1 MHz的双音信号加于功放的输入端来检验其线性度,其结果如图5示。由图5可以看出,在输出功率(Pout)为43 dBm时,对应于上边带(Upper Band)和下边带(Lower Band)的三阶互调失真系数(IMD3)分别为-30dBc和-33 dBc。图6为其功率附加效率(PAE)与输出功率之间的关系。我们之所以使用功率附加效率,是因为它在考虑功率消耗的同时,将其放大能力也计入其中。可以看出,在输出功率为43 dBm时,其功率附加效率为35%。这个值稍有点小,是因为为了确保较好的线性度,功放工作于甲类状态。

现在我们使用预失真器来对该功放进行线性化。其中,预失真器的电阻和电容要精心选择,取合适的值,以提供与功放相反的预失真特性。这里进行同样的测试,其结果如图7和图8所示。

图7 线性化后的功放的三阶互调失真系数与其输出功率之间的关系Fig.7 Linearized PA′s IMD3 vs.its output power

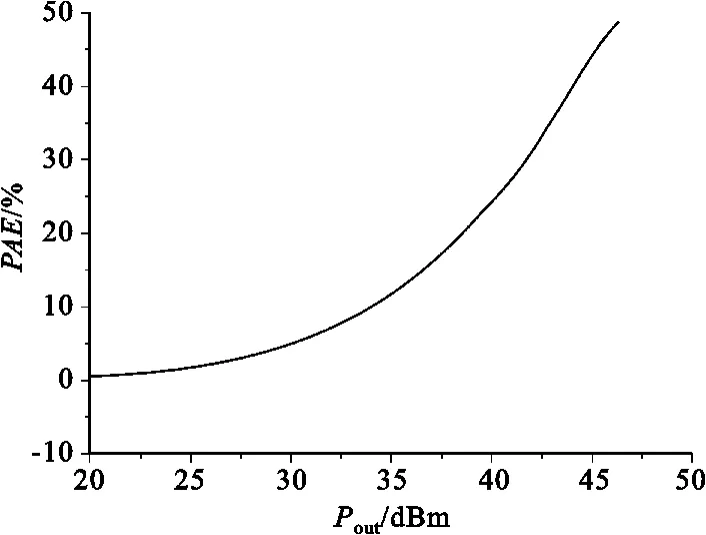
图8 线性化后的功放的功率附加效率与其输出功率之间的关系Fig.8 Linearized PA′s PAE vs.its output power

由图可以看出,线性化后的功放,在输出功率为43 dBm时,对应于上边带和下边带的三阶互调失真系数分别为-39.3 dBc和-43.5 dBc。显然,由于该预失真器优异的性能,功放线性度(三阶互调失真系数)得到了近10dBc的提高。此外,功率附加效率还略微提高,即36.8%,这可以通过非线性失真产物(如谐波、互调产物等)得到了抑制来解释。

5 结 论

本文在对功率放大器的非线性特性及其预失真线性化问题深入分析的基础上,提出了一种新的预失真器,该预失真器仅由一个二极管和分别与之串联和并联的电阻和电容构成。结合功放进行的双音测试验证了设计的有效性。与文献中已有的同类预失真电路相比,其结构简单,对功放的非线性改善明显。此外,理论分析部分得到的结论对同类电路的设计也具有指导意义。将这种预失真器与其它线性化技术相结合,以及引入自适应机制,将会得到更满意的结果。

[1]Peter BK.High-Linearity RF Amplifier Design[M].Norwood:Artech House,2000.

[2]CrippsS C.Advanced Techniques in RF Power Amplifier Design[M].Norwood:Artech House,2002.

[3]Hashmi M S,Rogojan Z S,GhannouchiF M.A flexible dual-inflection point RF predistortion linearizer for microwave power amplifiers[J].Progress In Electromagnetics Research C,2010,13:1-18.

[4]Yamanouchi S,Aoki Y,Kunihiro K,et al.Analysis and design of a dynamic predistorter for WCDMA handset power amplifiers[J].IEEE Transactions on Microwave Theory and Techniques,2007,55(3):495-503.

[5]SHEN Yi-ming,Hraimel B,ZHANG Xiu-pu,et al.A novel analog broadband RF predistortion circuit to linearize electro-absorption modulators in multiband OFDM radioover-fiber systems[J].IEEE Transactions on Microwave Theory and Techniques,2010,58(11):3327-3335.

[6]Chung Y,Jones J.Si-LDMOS high power amplifier RFIC with integrated analogue pre-distorter[J].Electronics Letters,2008,44(5):361-362.

[7]Bera S C,Singh R V,Grag V K.Diode-based predistortion linearizer for power amplifier[J].Electronics Letters,2008,44(2):125-126.

[8]Lee Y S,Lee M W,Kam S H,et al.A high-linearity wide band power amplifier with cascaded third-order analog predistorters[J].IEEE Microwave and Wireless Components Letters,2010,20(2):112-114.

[9]Park H C,Jung S C,Lim K H,et al.Analysis and design of compact third-order inter modulation generation circuits[J].Microwave and Optical Technology Letters,2009,51(9):2137-2140.