时间序列的单位根检验与伪检验

郭洪伟

（首都经济贸易大学统计学院，北京100070）

0 引言

经济分析中经常涉及时间序列的分析处理。不管是多变量的回归分析,还是用模型分析单个时间序列,都要先检验时间序列的平稳性。对于平稳序列和非平稳序列，在建模时需要给予区别对待。

如果一个时间序列的联合概率分布不随时间而变化，则称该时间序列是严格平稳的。如果时间序列变量的均值、方差和协方差不随时间变化,就可以认为该序列是弱平稳（或宽平稳）。通常情况下，我们所说的平稳指弱平稳。日常分析时，对于序列平稳性的检验，通常采用单位根检验检验方法。

假设随机过程{yt,t=1,2,…,n}满足yt=yt-1+ εt,其中,εt独立同分布,且E（εt） =0,D（ε2t）=E（ε2t) =σ2＜∞ ,则称 yt为随机游走过程。假设随机过程{yt,t=1,2,…,n}满足yt=ρyt-1+εt,其中εt为一均值为0的平稳序列,当ρ=1时，其滞后算子特征多项式存在一个单位根，此时称yt为单位根过程。可见,随机游走过程是单位根过程的特例。当ρ＜1时 yt是一个平稳序列，当ρ＞1时，yt是一个非平稳序列。如果时间序列是非平稳的,但经过一阶差分后成为平稳过程,则称该序列为一阶单整序列，记为I(1)。通过单位根检验判断序列平稳性的方法叫单位根检验。如果一个序列不管差分多少次，也不能变为平稳序列，则该序列为非单整序列。因为我们研究的经济数据非单整序列不多，本文不讨论非单整序列。

目前对单位根检验所采用的比较有影响的方法,主要有ADF检验、PP检验、KPSS检验及NP检验等。其中最常用的方法是ADF检验和PP检验。

ADF检验法是对DF检验方法的扩展,当序列残差项非白噪声时,为了消除残差项的自相关性,在回归模型等号的右边加入被解释变量本身的滞后项,将这一滞后项视为外生变量再进行检验,这样可以有效解决具有高阶自相关的时间序列问题。

ADF检验有3个辅助方程:

(1)无截距项和无趋势项

(2)仅含有截距项

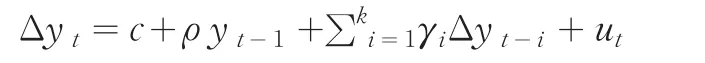
(3)含有截距项和时间趋势项

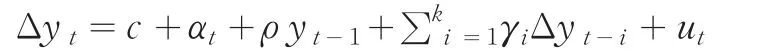
其中符号△表示一阶差分算子,c为截距项,αt为趋势项,∑ki=1γiΔyt-i为k个分布滞后项，ut为平稳的随机误差项,k为确定ut满足白噪声的最大滞后阶数。依据Schwarz或Akaike信息准则越小则表明模型越好。

ADF检验对于上述三个回归模型中ut有个基本假定：ut的方差相同。所以ADF检验只适用于方差齐性序列的检验。后来，Phillips和Perron对ADF检验统计量进行了非参数修正，得到PP统计量。利用PP统计量进行的检验叫PP检验。PP统计量不仅考虑到ut的异方差性，同时也考虑到自相关误差产生的影响，并与ADF统计量有相同的分布。PP检验的辅助方程与ADF检验的也类似。

需要指出的是，在使用ADF检验与PP检验时，特别要注意假设检验犯第二类错误（β错误）的风险。正如刘田（2008）的结论：ADF检验与PP检验对数据生成过程非常敏感,它们对线性趋势或无趋势平稳过程可以作出很好的检验判断。但对非线性趋势而言,如平方根趋势、二次趋势、对数趋势、分段线性的结构突变趋势等,ADF检验与PP检验趋向于将平稳过程判断为存在单位根,得出错误的检验结果[1]。不管是假设检验的第一类、第二类错误还是人为处理不当都会造成序列平稳性检验的伪检验，导致检验结论的错误。

1 时间序列平稳性的几个结论

时间序列的平稳性与其生成过程、时期跨度及后期的加工方法都有关系。为了判别、验证不同文献的检验结论，下面我们先证明与平稳性有关的几个结论。

定义 从一个完整的序列中连续抽取一部分数据构成的新的序列称为原序列的子序列。如对于序列{0,1,2,3,4,5,6},序列{1,2,3,4}是一个子序列，但{2,3,4,6}不是子序列。

结论1对于一个平稳时间序列yt(t=1,2,...,n)，其任何一子序列都是平稳序列。

证明：根据平稳序列的定义，可得yt的均值、方差、协方差有以下特点。

那么，对于任意一个yt的子序列xt,(t≤n),显然有：

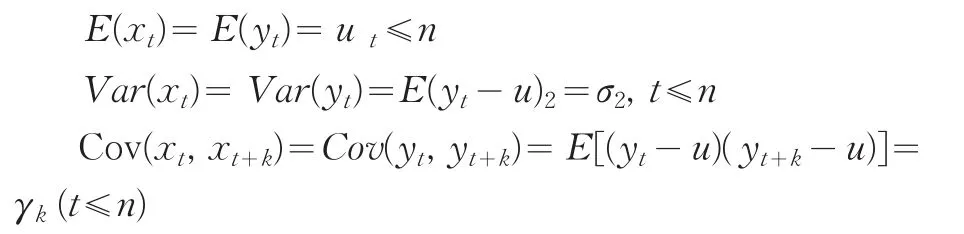
所以子序列xt为平稳序列。结论1得证。

根据此结论可知，文献[2]所述“由于样本区间选择的差异导致的错误”导致的伪检验是存在的。文献[2]中原作者对水平值DLPOW的1970～2006数据检验是平稳的，但对1978～2006这个子序列检验的结论是存在单位根。根据本文结论1，后者是前者的子序列，如果前者平稳的结论是正确的话，1978～2006也应是平稳的。这两个时间段的结论是相互矛盾的。从假设检验原理可知，第一类错误的概率不会大于α，一般来说拒绝原假设所犯错误概率小，所以“平稳”结论是正确的，而1978～2006这个子序列检验中是伪检验。一般来说是判定为有单位根（检验结论是非平稳）时，假设检验犯第二类错误风险较大。

根据上面结论1，可得如下推论。

推论 对于一个非平稳序列，任何以该序列为子序列的序列都是非平稳序列。

证明：设yt是个非平稳时间序列，yt是 zt的子序列。利用反证法。

如果zt是平稳序列，那么根据结论1，其子序列yt也是平稳的，这与yt是个非平稳时间序列矛盾。故推论1得证。

结论2对于一个时间序列yt，p为大于0的任意常数，则yt的每个值都乘以 p得到的新序列记为zt，则新序列zt与原序列yt平稳性相同，即原序列yt平稳则新序列zt也平稳，原序列yt非平稳则新序列zt也是非平稳的。

证明：假设yt是个平稳时间序列，p为大于0的任意常数，则有：

（1）均值E(yt)=u(t=1,2,...,n)

那么有：

所以zt也是平稳序列。

利用反证法，假设yt是个非平稳时间序列，如果zt是平稳序列，那么根据上面的结论用1/p去乘zt也应是平稳的，即yt也应是平稳，与前述矛盾。所以zt与yt一样非平稳。综上，结论2得证。

结论3对于一个d阶单整时间序列yt,对于其任何一子序列zt，设zt的单整阶数为k，则有k≤d。

证明：设有一个d阶单整时间序列yt，记为I(d)，yt的d阶差分序列记为ydt则根据单整定义ydt为I(0)，即是个平稳序列。

设zt为来自于yt的任一子序列，记zt的d阶差分序列为zdt。显然，zdt是ydt的子序列。根据结论1，因为ydt是平稳序列，所以zdt也是平稳的。所以zt的d阶差分序列平稳，但我们不知其d-1阶差分是否平稳，所以不能肯定zt是 I（d）.假设zt是 I（k）,我们肯定有k≤d。因为若k＞d，zt的d阶差分序列不可能是平稳的。结论3得证。

根据结论3，文献[3]所说的“伪检验”可能不存在。原作者把LGDP的样本期间由原来的1978～2004年缩短为1992～2004年,检验结论由不平稳变为平稳，并把此称为“样本区间选择带来的错误”。根据结论3，把样本期间缩短，LGDP序列的单整阶数不会高于原来的阶数，如果原序列是不平稳的单整序列，其子序列可能是平稳的也可能非平稳，这都不矛盾。这不能说检验方法出了问题，更不能称之为“伪检验”。

2 文献中我国GDP数据序列的伪检验

国内生产总值（GDP）,是指按市场价格计算的一个国家或地区所有常住单位或产业部门在一定时期内生产活动的最终成果。GDP作为一个国家或地区经济总量的最重要的度量指标，在各种经济分析文章中被经常使用。我们知道支出法计算的GDP数据和收入法计算的会有差异，各地方统计数据和国家统计数据也有出入。笔者无法获得所有后附参考文献的原始数据，所以本文以下的分析，假设所有人使用的原始数据没有差异。

分析GDP序列首先要做的是对数据的加工和检验。GDP数据的加工主要分三步：

第一步，根据价格指数调整，剔除价格因素；

第二步，季节调整，去除季节因素（季度数据时）；

第三步，自然对数变换，减除数据系列的异方差性，使数据更平稳。

笔者对我国1952～2008年的GDP数据及人均GDP数据进行了实证检验。数据来源于国泰安信息技术有限公司的《中国宏观经济研究数据库》（2010版）。在检验之前对GDP数据序列（记为GDP）及人均GDP数据序列（记为RGDP）进行了加工。以1952年为基期的价格指数剔除价格因素影响，得到实际GDP和实际人均GDP序列，分别记为SGDP、SRGDP。然后利用SGDP计算实际GDP年度增长率，记为DGDP。显然，DGDP是从1953年开始到2008年的一个数据序列。对SGDP、SRGDP取自然对数，分别记为LNSGDP、LNSRGDP.我们主要探讨DGDP、LNSGDP和SRGDP、LNSRGDP四个序列的平稳性。本文所有数据利用Eviews6.0处理,下面给出了检验结果。

2.1 LNSGDP的单位根检验

经检验LNSGDP原序列非平稳，对其一阶差分的ADF检验结果如表1。

从检验结果看，LNSGDP序列是I（1）序列，这与大部分文献的检验结论相同。利用本文结论3的结论，可知1952～ 2008间任一子序列要么是I(1),要么是平稳的。但是文献[4]、文献[5]、文献[6]都认为取对数后的GDP序列是I（2）序列。这明显与笔者检验结论矛盾。他们利用的数据都是笔者所用序列的一个子序列，他们的检验结论不应该和此结果矛盾。仔细研究发现文献[4]和文献[6]的数据没有利用价格指数调整,根据本文结论2，价格调整对序列平稳性应该没有影响，但是这里还要取对数，此时价格平减的影响就很难说了。实际上，我们应该先通过价格指数平减，然后再取对数，这样LNSGDP序列应是I(1).文献[5]先发现LNSGDP不平稳，后检验LNSGDP的二阶差分平稳，但他们没有发现LNSGDP的一阶差分也平稳，所以他们把LNSGDP错判成I(2)序列。这里要指出的是，文献[7]考虑结构突变的检验结论也与此并不矛盾。文献[7]认为我国1952—2004的实际GDP的对数序列是围绕着1个或2个结构断点的分段趋势平稳序列。我们知道分段趋势平稳，单位根检验的结果时不平稳的，但通过差分分段趋势差异消除后，应该是平稳的，所以有结构断点的分段趋势平稳序列的单位根检验结果是I（1），有的文献把这个检验也称为伪检验[8]。笔者对此观点持不同看法。

表1 △LNSGDP检验结果

2.2 DGDP的单位根检验

这里要说明的是，DGDP是实际GDP的年增长率，不是实际GDP的一阶差分。DGDP原序列的ADF检验结果如表2。

经检验DGDP为平稳序列。根据本文结论1，DGDP的子序列也是平稳序列，所以我国1953～2008年期间任何一时间段的实际增长率序列（DGDP）都应该是平稳的。但文献[9]认为真实GDP计算的增长率是I(1)序列.文献[9]分析1995年第1季度到2008年第4季度季的度数据，季度数据不能和笔者年度数据检验结论直接比较。文献[10]也分析季度数据，利用1979年第1季度到2009年第3季2009年第3季度GDP增长率数据，经检验调整后的GDP增长率数据具有整体平稳性，即是I（0）序列。文献[9]的数据是文献[10]数据的子序列，根据本文结论1，如果文献[10]结论正确，文献[9]的检验结论也应是平稳的，但实际不然。若不考虑其他原因，他们两方至少有一方检验是伪检验。仔细研究发现文献[9]使用季度数据但没有进行季节调整，这可能是问题的原因所在。

表2 DGDP的检验结果

2.3 SRGDP、LNSRGDP的单位根检验

对实际人均GDP序列（SRGDP）进行检验，其原序列和一阶差分序列都是非平稳的，对其二阶差分序列ADF检验结果如表3。

对实际人均GDP自然对数序列（LNSRGDP）进行检验，其原序列是非平稳的，对其一阶差分序列ADF检验结果如表4。

若考虑到SRGDP可能存在的异方差性，笔者也利用了PP检验法分析SRGDP序列，结果与上面类似，具体数据略。从上述检验结果可知SRGDP为I(2)序列,LNSRGDP序列是I（1）序列。根据结论3，SRGDP的子序列可能是I(2)，也可能是I(1),或者是I (0).对于具体的SRGDP的子序列要具体分析。但是对于一个固定的子序列只能是上面的三者之一。文献[11]分析1981～2007年间年度数据，原作者认为年度人均实际GDP一阶单整，即是I (1)序列。这并不与笔者检验结论矛盾（即使王冬生得出I(2)的结论与笔者也不矛盾）。但是文献[12]检验1986～2006年的SRGDP是I(2).而文献[10]判定1981～2007年的SRGDP为I(1).前者的序列正好是后者序列的一个完整子序列，根据本文结论3，此二位作者的结论矛盾，可能有一方的单位根是伪检验。仔细分析发现，文献[11]没有发现人均GDP异方差性，用ADF方法检验不合适，所以与文献[12]用PP检验的结论矛盾。文献[7]认为我国1952～2004年实际人均GDP的对数序列是围绕着1个或2个结构断点的分段趋势平稳序列。正如前面LNSGDP检验中论述的一样，笔者认为这与本文的结论“LNSRGDP是I(1)序列”不矛盾。

表3 SRGDP序列检验结果

表4 LNSRGDP序列检验结果

3 结束语

本文分析了时间序列平稳性检验与伪检验。我们知道数据序列期间选择的不同或对数据的加工处理不一致，会导致不同的检验结论，但不同的结论不能说明单位根都是伪检验。GDP序列作为基础数据，是分析其他经济问题的前提，如果有关GDP序列的检验出了问题，那以后的结论可想而知。笔者通过对我国1952～2008年的GDP数据分析，得出有关GDP的检验结论：实际人均GDP及取对数序列分别为I (2)、I(1)序列，实际GDP取自然对数序列为I（1）序列，实际GDP增长率（DGDP）是平稳序列。在具体分析某个时间段GDP数据时，可利用本文的结论相互验证，避免伪检验的发生。

[1]刘田.ADF与PP单位根检验法对非线性趋势平稳序列的伪检验[J].数量经济技术经济研究，2008，(6).

[2]吴翔.单位根检验中的误检验—以我国年发电量时间序列为例[J].东北电力大学学报，2008,(2).

[3]徐炳胜.单位根“伪检验”解析--以GDP时间序列为例[J].数量经济技术经济研究，2006,(5).

[4]徐凤,金克琴.中国居民消费与经济增长关系的实证研究[J].北京工商大学学报社会科学版，2009,(3).

[5]郝香芝,李少颖.我国GDP时间序列的模型建立与预测[J].统计与决策，2007,(23)

[6]龙莹.我国固定资产投资与国内生产总值关系的协整分析[J].统计与决策，2005,(3).

[7]梁琪,滕建州.中国宏观经济和金融总量结构变化及因果关系研究[J].经济研究，2006,(1).

[8]张建华,涂涛涛.结构突变时间序列单位根的“伪检验”[J].数量经济技术经济研究，2007,(3).

[9]唐志军,徐会军,巴曙松.中国房地产市场波动对宏观经济波动的影响研究[J].统计研究，2010,(2).

[10]王成勇，艾春荣.中国经济周期阶段的非线性平滑转变[J].经济研究，2010,(3).

[11]王冬生.中国信贷市场发展与经济增长：1981～2007[J].统计与决策，2010,(3).

[12]潘省初.计量经济学中级教程[M].北京：清华大学出版社，2009.