低碳经济下的供应链协同研究

章文燕

（台州职业技术学院，浙江 台州 318000）

0 引言

供应链是由供应链和需求链组成的，各实体为了实现自身利益最大化，各自为政，产生了木桶效应，从而导致供应链的收益下降。那么，当供需双方的经济利益以及环境因素相冲突时，什么是更好的解决方案？

因此为了优化供应链，降低碳排放量，每一个供方在优化自身局部目标的同时，还要考虑与其他成员协同运作，从而达到供应链整体的优化目标。低碳供应链对于实现经济的可持续发展具有重要的意义；供应链协同能给整个供应链带来许多利益如缩短上市周期、降低库存水平、加快周转、降低劳动强度、增强竞争力、特别是减少碳排放量。因此，研究低碳经济下的供应链协同对推动当前经济的发展有着深远的意义。

1 低碳经济下的供应链协同最优订货量

1.1 假设

由供需双方构成的供应链协同系统，假设市场需求可以被充分满足。本文建立的模型目的是在考虑碳排放的约束下，如何通过供需双方的协同达到整个系统利润的最优？

模型假设如下：

(1)供需双方均是理性的“经济人”

(2)顾客接受自由竞争市场中的价格

(3)市场上对某产品的年度需求量为单位，且需求均匀分布

(4)供方的年度产能为y单位，满足y＞x

(5)买方市场

(6)系统考虑碳排放的约束。

符号设定如下：

P：需方定价；

A1：需方每次订货所花费的固定成本；

B1：需方年度单位库存保管费用；

P1：供方给予需方的单位产品批发价；

Q：需方的订货批量；

A2：供方每次处理需方订货所花费的固定成本；

A3：供方每次生产准备所花费的固定成本；

B2：供方的年度单位库存保管费用；

C1：供方每件产品的生产成本；

Q1：供方生产批量；

C2：供方生产单位产品的碳成本；

C3：：（供方或者需方）单位库存所产生的碳成本；

C4：需方单位距离运输产生的碳成本；

L：表示供方与需方的距离；

U：单位距离的运输成本；

T：供应链系统的利润；

T1：供方的利润；

T2：需方的利润。

1.2 非协同下双方的最优批量模型

1.2.1 需方的最优订货批量模型

当供方没有提供数量折扣时，需方的年利润为：

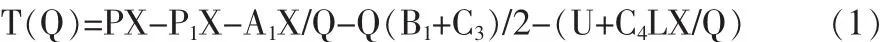
其中，PX为需方的年销售收入，P1X为年采购成本，A1X/ Q为年订货成本，Q（B1+C3）/2为年库存保管成本,（U+C4）LX/ Q为年运输成本。

对Q求导即可得需方的最优定购批量：

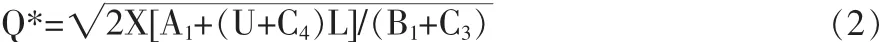
将Q*代入到式（1）中，可得需方最优的年利润为：

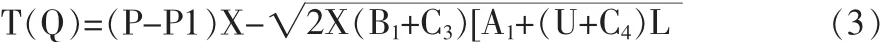
1.2.2 供方最优生产批量模型

在买方市场上，如果供需双方未达到协同合作，则供方应在需方已做决策的条件下，追求自己利润最大化的决策。

著名的美国供应链管理专家Lee教授认为，当供方的经济生产批量为每次需方订货量的整数倍，即Q1=KQ（K≥1，且K为整数）。供方的年平均库存为：

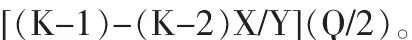
因此供方的年利润可以表示为：

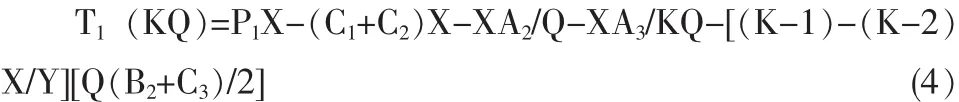
其中，P1X为供方的年销售收入，年生产成本为（C1+C2）X，年订单处理成本为XA2/Q，XA3/KQ为年生产准备成本，[（K-1）-（K-2）X/Y][Q（B2+C3）/2]为年库存保管成本。

同时设经济定购批量Q*为需方的定购量，则供方的利润为：

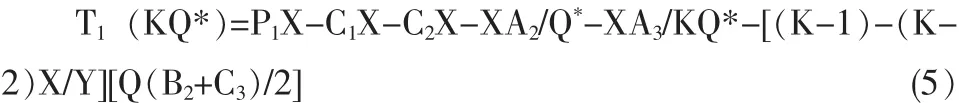
对上式K求导可得：

将上面的结果代入到Q1*=KQ*中，可得供方的最优生产批量为：

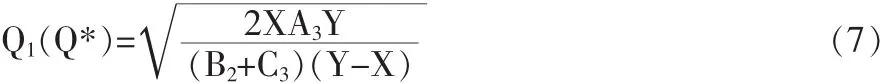
对(4)式中的Q求导可得：

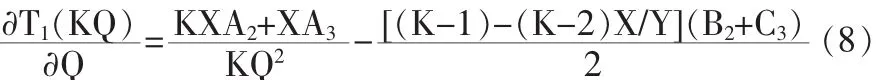
将Q*的表达式代入（8），要使供方的利润函数T1（KQ）在需方的最优定购批量为Q*时最大化，由导数为零得到如下结论：

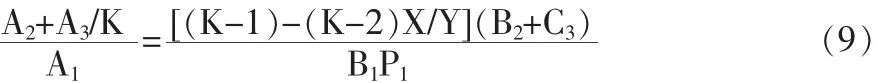
上式中，由于供方是理性的，所以：

已知为正整数，则上式在一般情况下很难成立，供方利润很难达到最优。从而整个供应链系统的利润也没有达到最大化。通过供方与需方的协同，我们可以使供应链系统和供方的利润都得到改进。对于供方而言，可以通过提供数量折扣的方法来获取最优利润，即为了提高利润，我们可以通过把数量价格折扣给予需方，达到扩大销售量来实现。

1.3 协同下双方的最优批量模型

根据以上分析，在买方市场不集中且无折扣的非协同条件下，对于供方来说成本相对较高且处于被动局面，；需方则处于最优决策之中，此时整个供应链系统不能达到最优。同样分析在卖方市场时我们也能得到整个供应链系统未能到最优。

供应链协同理论是要达到整个供应链系统的利润最大化，因此需要对上述供应链系统进行改造，即要实现供应链最大绩效，必须使各成员都从供应链的利益最大化来进行一系列活动。但事实却非如此，因为供需双方并并不是象我们所假定的理性“经济人”。如果需方订货量增大，虽然对供方降低成本非常有利，但这却不利于需方利益。因此，我们可以通过供方可以给予需方适量的价格折扣来达到供应链优化的目的，一方面可以提高供方利润，一方面降低需方的采购成本和订货成本，从而实现双赢。

我们假设原最优订货批量的M倍(M≥1)是供方要求的订货批量，其折扣如下所示：

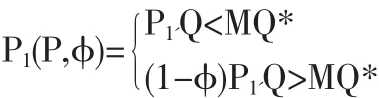
1.3.1 需方利润分析

当供方要求订货量无数量折扣且增大M倍而时，需方的年利润函数变为：

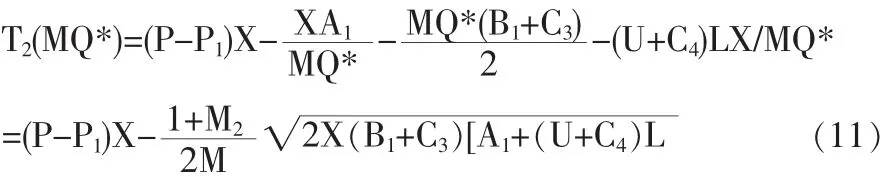
由于M≥1所以T2(MQ*)≤T2(Q*)，需方年利润的减少额为：

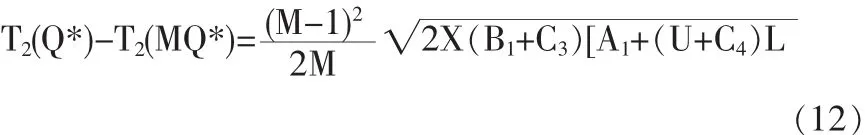
因此供方要使需方增大订货量，必须提供数量折扣。而且在此折扣下需方的年利润增加额（年采购成本减少额与年库存费用节约额之和）必须大于需方在没有数量折扣时增加订货量到MQ*导致的年利润减少额。即：

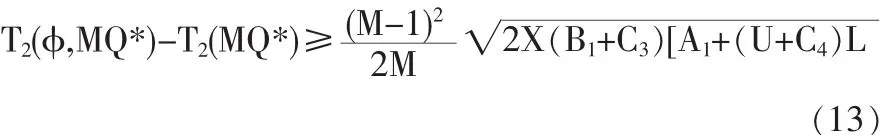
化简上式可得：

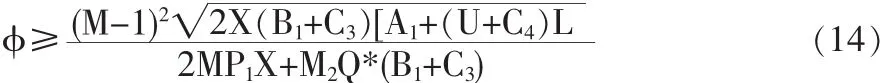
由此我们可以得到需方来说是“盈亏平衡”的折扣率：

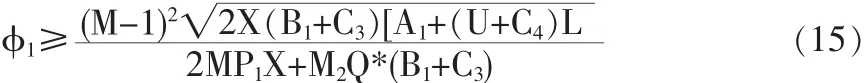
1.3.2 供方利润分析

前面求出了没有折扣契约，需方的定购量为Q*时，供方的最优生产批量为：

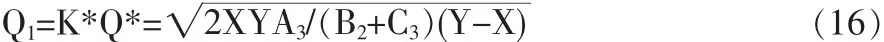
供方向需方提供数量折扣λ、需方的订货量增大到KQ*后供方的利润函数为：

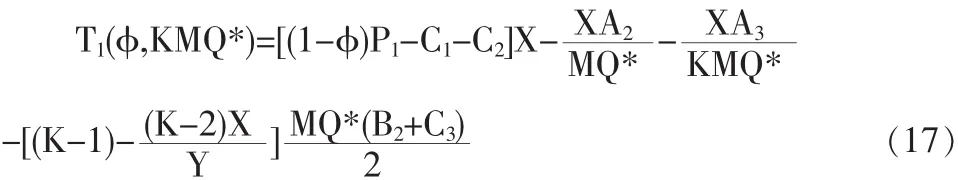
对上式中的K求导，可以得到供方利润最大化时K'的表达式为：

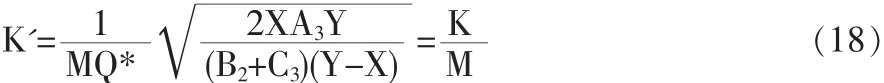
供方提供数量折扣后的利润应该至少不小于折扣前的利润：

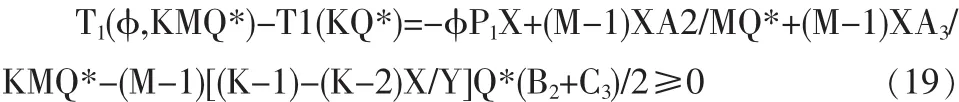
化简并将K的表达式代入可得：

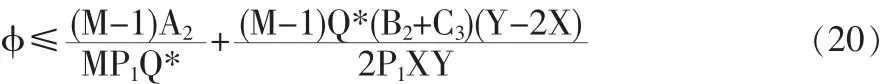
因此供方的“盈亏平衡”折扣率为：

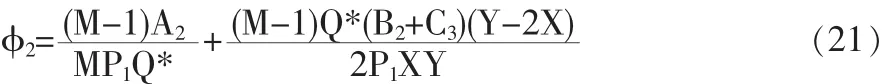
1.3.3 数量折扣契约设计

综合式(14)和(20)，我们在M的取值范围内选取某一合适的K*，即要求需方增大订货量至M*Q*，此时，需方的年利润减少额小于供方的年利润增大额，因此通过协同合作可以使供应链的总利润增大。

因此，只要φ1≤φ≤φ2，并且选择适当的φ，供方与需方的利润就都会有不同程度的增加，从而供应链系统的总体利润也实现了提高。

所以，数量折扣契约可以设计为：

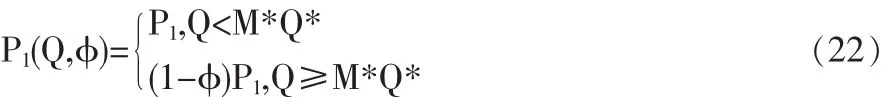
其中φ的具体取值取决于供需双方的博弈力量对比和双方对提高供应链利润的贡献大小。

根据上述的模型研究，可以得到在供需双方在协同合作条件下，可以使低碳供应链的利润最大化，相关结果如图1所示：

图中灰色曲线的含义是在没有协同情况下单个企业的经济订货批量其中为没有协同下的供应链总体最优订货批量。从图中可以看出的是。在整个供应链的利润达到最优情况时，供应链中的个体效益实际上不是最优，也就是说企业牺牲了自己的利益来满足了总体需求，在这种情况下会打击上下游企业协同的积极性。但是如果在低碳供应链协同的情况下（红线表示在低碳情况下的利润函数图），由于碳成本的存在，供应链的最优订货批量为,而此时单个企业的利润不低于低碳前的利润，而且也达到了整个供应链利润的最优。

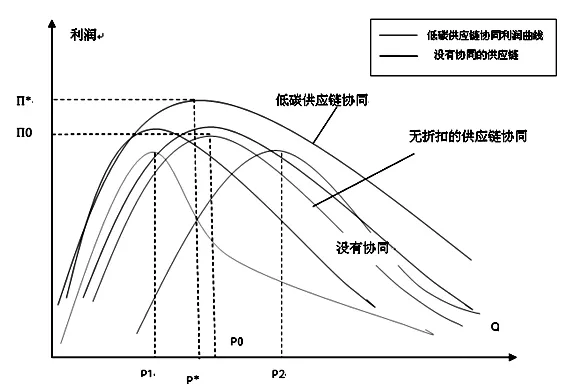
图1

2 低碳供应链协同的算例

为了验证模型的可靠性，下面我们来进行数据测试。对数据使用规划求解模型进行求解，得出最终数据。从实验的结果我们可以看出，整个模型的建立还是比较可靠的。

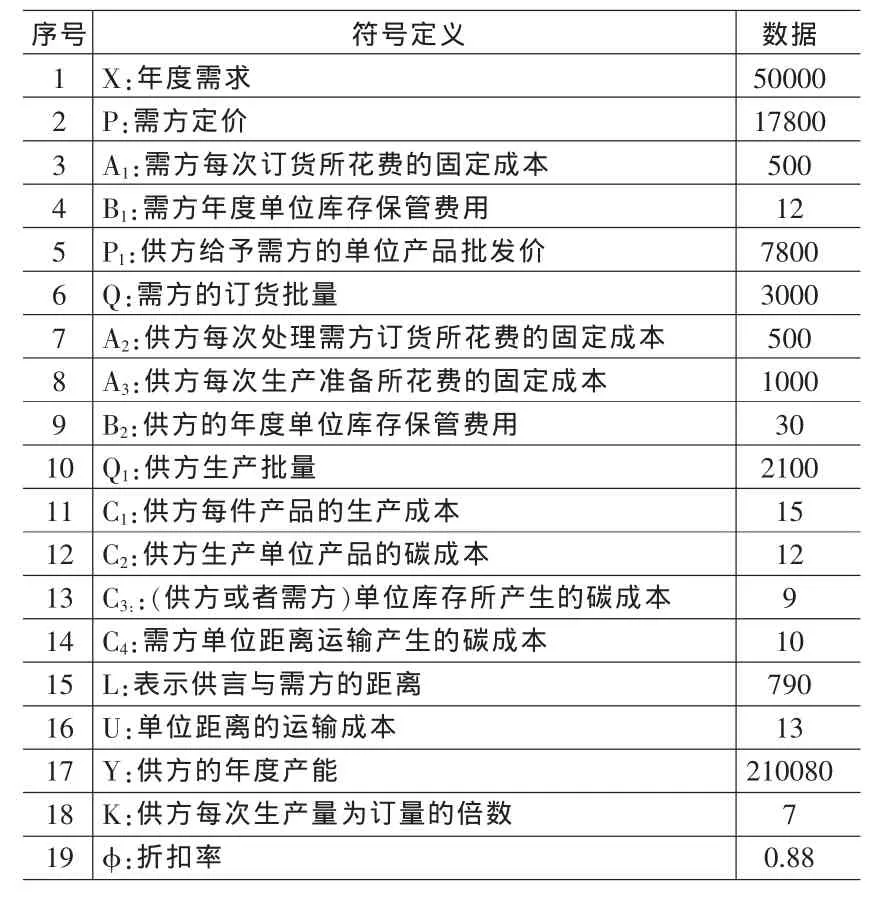
表1

参数定义如下表1：

经过软件的规划求解，运算结果如下：

从运算结果可以看出在低碳供应链协同中实施折扣后的单企业的在低碳供应链的最优订货批量时的利润要比实施折扣前的利润高，而且供应链的利润在实施折扣后的利润比折扣前的利润也得到增加。这说明在低碳供应链协同下实施订货折扣不仅能提高供应链的整体利润，而且能提到单个企业的利润。这也验证本模型的可行性。

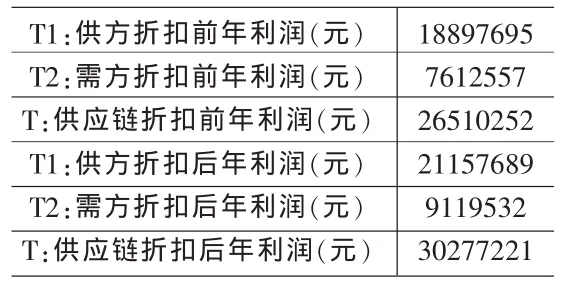
表2

3 结论

研究显示，在供需双方之间的协同下，利用折扣可以在实现供应链整个系统利润的最大化，在供需双方利润不受影响的情况下，把供应链总体碳排放降至最低限度。

[1]Togar,Ramaswami.Design for Supply Chain Collaboration[J].Business Process Management Journal,2008,(3).

[2]D iane Mollenkopf,Wendy L.Green,Lean,and Global Supply Chains[J].Physical Distribution&Logistics Management,2010,(1).

[3]马祖军.供应链中供需协调及数量折扣定价模型[J].西南交通大学学报,2004,(4).

[4]金强.供应链管理中数量折扣契约设计[C].上海海事大学硕士学位论文,2006,(6).

[5]田军.基于供应链管理的最优契约定价模型研究[J].中国科学管理,2005,(10).