一种基于跟踪精度控制的组网火控雷达抗ARM方法
熊久良,徐 宏,韩壮志,何 强,封吉平
(军械工程学院光学与电子工程系,石家庄 050003)
1 引 言
火控雷达作为现代地面防空系统的重要组成部分,通过有源辐射方式完成对目标的精密跟踪,控制武器系统对目标进行打击。与警戒雷达不同,火控雷达工作时通常采用对目标持续照射的方式,所以反辐射导弹(Anti-radiationMissile,ARM)能够更加容易地利用雷达辐射的电磁波发现、跟踪并摧毁火控雷达。因此,寻求火控雷达对抗ARM的有效方法成为国内外重要的研究课题[1]。
目前,国内外研究集中在对ARM的低截获、诱偏等对抗技术上,而均未研究如何能够在提高雷达生存能力的同时,保持雷达的跟踪能力[2]。并且当前组网理论的研究集中在警戒雷达,缺乏对火控雷达组网的应用研究[3]。基于此,本文提出基于跟踪精度控制的组网火控雷达间歇式目标跟踪方法,即组网火控雷达通过间歇辐射方式对同一目标进行跟踪,在保证一定跟踪精度的同时,尽量减少雷达辐射时间,降低雷达信号被截获的概率,实现目标跟踪与电子反对抗的有效结合。
2 组网火控雷达间歇工作机理分析
2.1 单部火控雷达间歇工作原理
与警戒雷达不同,火控雷达通常采用自动角度测量方法使雷达天线自动跟踪目标,快速连续地提供单个目标的精确三维坐标测量数据,以供防空武器系统使用[4]。具体工作原理如图1所示。
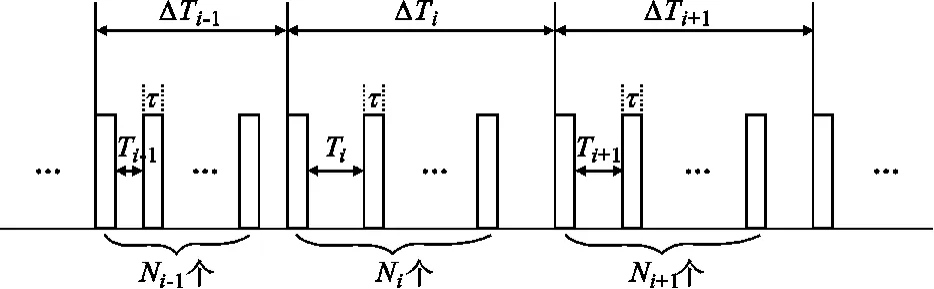
图1 火控雷达工作原理Fig.1 Working theory of fire-control radar
图中,脉冲宽度为τ,ΔTi为采样时间间隔,对应的脉冲个数为Ni,则相应的脉冲平均重复周期Ti=ΔTi/Ni。正常辐射状态下 ,ΔTi、Ni、Ti均为恒定值。此时脉冲信号以固定重复周期进行发射,并且全部用来进行目标跟踪。与此同时,雷达将一定时间间隔对应的采样点数据传送到数据处理中心。而在间歇辐射状态下,采样时间间隔Ti将根据跟踪精度而实时地自适应变化,以确保火控武器系统有效打击目标所需要的跟踪精度,同时最大限度地降低雷达信号的被截获概率。假定每个采样时间间隔ΔTi内脉冲的发射个数为固定值N,则间歇式目标跟踪可以看作是通过自适应改变脉冲重复周期Ti,以保证对反辐射导弹载机的跟踪精度,同时尽量提高雷达的低截获性能,以有效对抗ARM。
2.2 组网火控雷达间歇工作机理分析
文献[2]指出,组网雷达间歇辐射实质上是对雷达进行辐射控制的结果,从窗口函数的理论出发,相当于在原有雷达脉冲窗口函数的基础上,再附加一个辐射时间控制窗口。如图2所示,假设由3部火控雷达进行组网,各雷达进行间歇工作,而各个雷达的工作时间由融合中心进行控制。
从图中可以看出,在每一个辐射控制周期 TC内只有一部雷达工作,工作雷达采用间歇工作方式,并将得到的采样数据实时通过融合中心传送到其它雷达,当前雷达停止工作后,下部雷达立即工作,如此循环进行,融合中心将得到完整的目标信息。可以看出,对于系统中的单部雷达而言,其间歇过程不仅包括自身工作时间内的间歇,也包括其它雷达工作时的间歇。相对于单部火控雷达间歇工作,组网条件下单部雷达能够获得更长的间歇时间,得到更高的低截获性能。
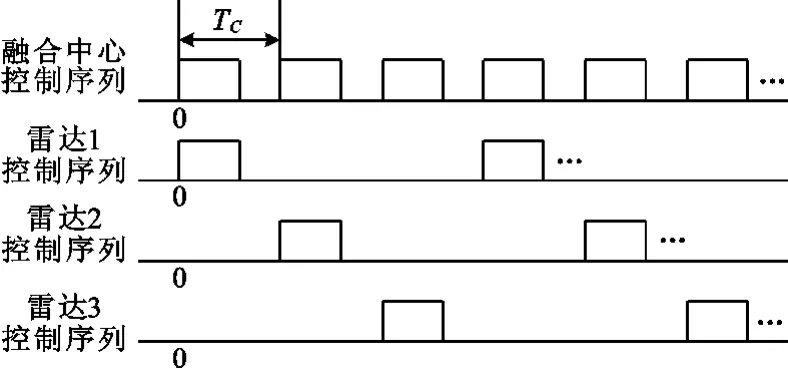
图2 雷达组网系统间歇辐射工作时序Fig.2 Working scheduling of fire-control radar network
在图2中辐射控制周期TC取固定值,实际中,TC的值可能是变化的,甚至是随机变化的。图中,各雷达是轮替工作的,并且认为当前雷达停止工作后,下部雷达立即工作,忽略了轮换过程中调整时间的影响,本文仅对此种情况进行研究。
3 评价指标
为有效评价本文提出的跟踪方法的性能,现定义如下评价指标作为跟踪效果的度量指标。
3.1 跟踪精度
跟踪精度可以用来衡量雷达对目标的可靠跟踪效果,文献[5]指出可以用滤波误差协方差来描述目标的跟踪效果。因此,本文采用滤波误差协方差来定义系统对目标的跟踪精度。
设T时刻的跟踪滤波误差协方差为P(k/k),则定义该时刻系统的跟踪精度C(k)为
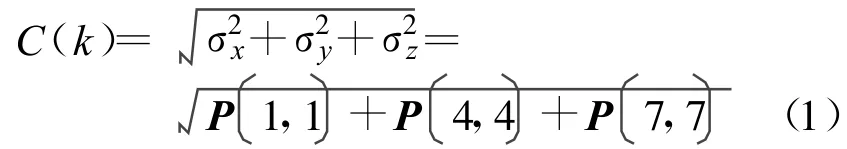
在实际作战过程中,为了满足要求的打击效果,防空武器系统对雷达的跟踪精度通常会有一个最低标准m,只有满足C(k)≤m,防空武器系统才能对目标进行有效打击。
3.2 截获概率
文献[6]认为信号的前端截获属于多维空间中的几何概率问题,只有当空域、时域、频域等所有的因素同时满足的情况下才可能发生,因此可以采用窗口函数模型来描述。针对火控雷达的工作特点,仅需考虑雷达脉冲窗口函数和侦察系统频率搜索窗口函数。
假设雷达脉冲宽度为τ,脉冲重复周期为T,并采用固定载频;侦察系统频率搜索周期为Tf,并以Δfe的瞬时频率带宽搜索Δf的频率范围,可得两窗口同时重合的平均周期为

则在t时间内至少发生一次截获的概率为
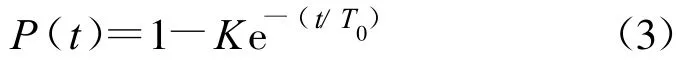
式中,K=1-P(0),P(0)是一次截获发生在开始瞬间的概率。
实际情况下,侦察系统的前端截获概率达到一定门限值P0时其截获过程才能算是有效的。针对此情况,本文设定典型截获概率门限值P0来控制雷达工作时长,并通过比较到达P0所用的时间长度来客观评价截获性能的高低。
3.3 截获概率密度
由公式(3)可以看出,前端截获概率是统计意义上的概率的累加值,当时间足够长时,其值会趋于100%而不再变化。为能够在整个仿真时间内评价跟踪性能,本文定义截获概率密度作为补充评价指标。
设在每个采样时间间隔ΔTi内,火控雷达以固定的间隔Ti发射N个脉冲,雷达信号的平均截获概率密度为ρ,则依据概率理论可得如下关系:
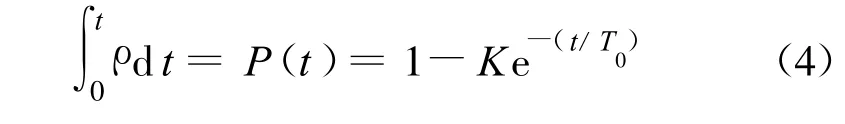
从而可以求得在采样时间间隔ΔTi内的平均截获概率密度的计算公式为
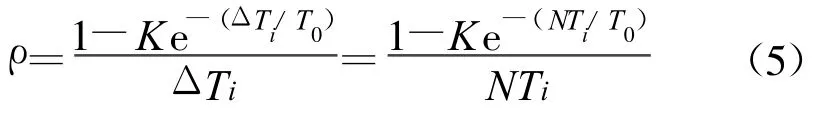
可以看出,平均截获概率密度ρ表示单位时间内雷达信号被侦察系统截获的概率,其值会随着采样间隔或发射脉冲间隔的自适应调整而发生变化,因此可以在整个仿真时间内实时地评价目标的跟踪性能。
4 目标模型及采样间隔的选取
为简化目标运动模型,凸显本文提出的跟踪方法的有效性,本文采用简单的常加速模型对反辐射导弹载机进行建模,并结合标准卡尔曼滤波形成闭环的目标跟踪算法。本文不对算法进行具体介绍,详细公式可参考文献[7]。
从间歇辐射机理可以看出,实现间歇式目标跟踪的关键在于采样间隔的自适应变化。在实际工作过程中,由于目标跟踪精度的要求和雷达本身性能的限制,采样间隔将会限制在内。自适应调节采样间隔的难点在于如何在固定取值区间内,判断何时开始提高或减小采样间隔以及采样间隔的调节量。
Cohen在文献[8]中提出用递推公式进行采样间隔的自适应确定:
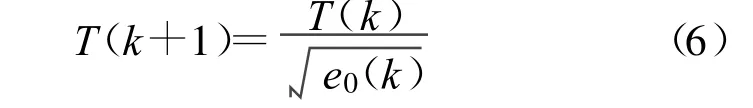
式中,e0(k)=e(k)/σk,σk为目标径向距离量测噪声的标准差,e(k)为滤波残差。
从式(6)可以看出,下一时刻的采样时间间隔由上个采样时间间隔和残差的比值得到,此方法有较好的自适应变化能力和实时性。本文中提出的间歇式目标跟踪需要使跟踪精度限定在一个固定门限之下,根据上式的启发,本文将递推公式改进为

式中,C0(k)=C(k)/m,C(k)为k时刻的跟踪精度,m为设定的跟踪精度门限,η为调整因子,其值可由仿真结果进行调整。
从式(7)可以看出,该递推公式的实质是将跟踪精度对固定门限值进行归一化。当跟踪精度高于门限值时,下一时刻采样间隔减小;当跟踪精度低于门限值时,下一时刻采样间隔增大,并且其变化程度可由调节因子进行调节。
5 仿真分析
为了说明文中提出的跟踪方法的有效性,本文在相同条件下将间歇式跟踪与常态下的固定采样跟踪进行仿真对比。
假定组网系统由3部火控雷达组成,成正三角形布局,不考虑雷达间信息传输延迟,雷达1首先工作,采用轮换工作方式。脉冲重复周期T=1 ms,每隔N=2个脉冲进行一次数据处理,因而固定采样周期为T1=NT=2ms。递推采样周期上下限分别为 Tmin=2 ms、Tmax=0.4s,采样间隔初始值T2(1)=0.1s,跟踪门限值 m=5 m,调整因子 η=1,各雷达观测噪声矩阵分别为
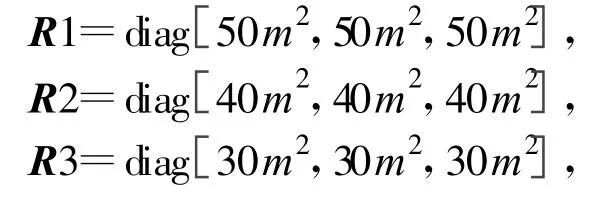

仿真时间为 tmax=50s,进行50次Monte-Carlo仿真,结果如图3~7所示。其中,图3~5为整个组网系统的仿真结果比较图,图6和图7为雷达1的仿真结果比较图。

图3 目标跟踪轨迹Fig.3 Target tracking trajectory

图4 跟踪精度Fig.4 Tracking accuracy

图5 脉冲重复周期Fig.5 Impulse repetition period
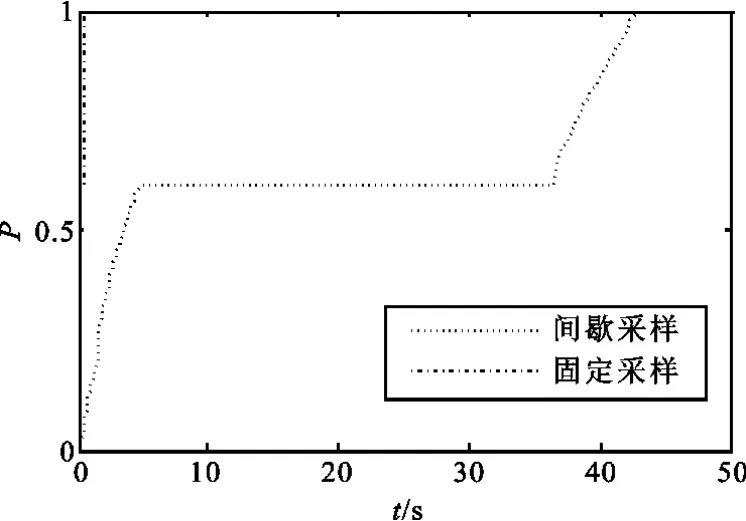
图6 雷达1截获概率Fig.6 Intercept probability of radar 1
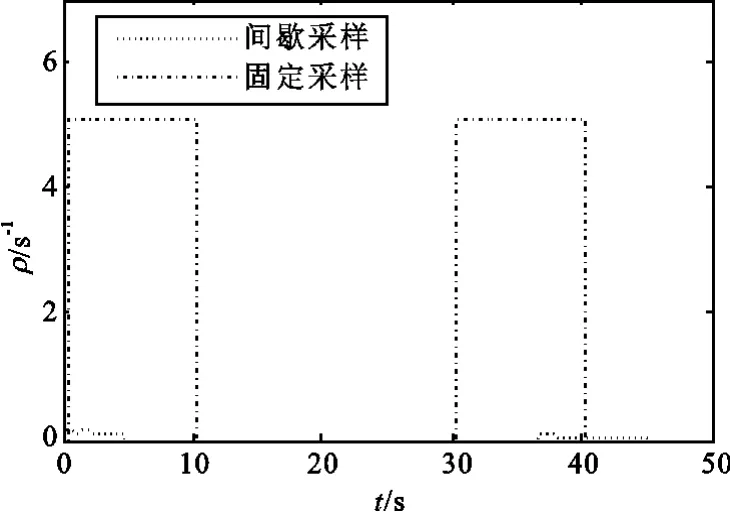
图7 雷达1截获概率密度Fig.7 Intercept probability density of radar 1
从图4中可以看出,两种跟踪方法下的跟踪精度都满足火控系统的要求。并且,在第一个轮换周期内,组网雷达约在5 s、16 s、37 s进行了工作轮换,轮换时刻工作雷达的截获概率正好达到 P0左右,这也证明了文中所提的由截获概率典型值来控制雷达工作时间的正确性。
对比图5、图6和图7可知,在雷达工作时间内,截获概率随着时间的增长而增长,并且当时间足够长时,会为恒定值100%而不再变化,而截获概率密度在整个仿真时间内都能有效地评价跟踪效果,这与文中的理论分析是一致的。对整个组网系统而言,平均脉冲重复周期约为100 ms,平均截获概率密度约为0.12 s-1,而固定采样的采样时间为1 ms,截获概率密度为5 s-1,这些数据都证明了本文所提出方法的有效性。
从雷达1的仿真结果可以看出,在单部雷达工作期间,雷达1截获概率到达P0的时间约为5 s,远远高于固定采样下的0.12 s,并且从整个仿真时间来看,雷达1截获概率到达 P0的时间将被延长至37 s左右,这说明虽然单部火控雷达进行间歇式目标跟踪可以有效降低信号的截获概率,但其效果是有一定局限性的,组网技术的应用可以很好地解决单部雷达的局限性问题,进一步提高信号的低截获性能。
6 结 论
本文基于跟踪精度控制,提出了组网火控雷达间歇式目标跟踪方法。仿真结果表明,该方法既可以保证火控雷达对反辐射导弹载机的正确跟踪,为火控系统准确打击提供保障,同时又能提高对抗ARM的效果。从仿真结果中还可以看出,组网中雷达工作顺序、雷达的布局以及组网雷达数目都可能对跟踪效果产生影响,其影响机理及程度如何有待进一步研究。
[1]王智,朱宏,许建明.防空雷达抗反辐射武器对策分析[J].航天电子对抗,2005,21(5):7-9.WANG Zhi,ZHU Hong,XU Jian-ming.Analysis of Countermeasures of Air-Defense Radar Against ARW[J].Aerospace Electronic Warfare,2005,21(5):7-9.(in Chinese)
[2]沈阳,陈永光,李修和.组网雷达抗ARM工作模式设计及仿真研究[J].系统工程与电子技术,2004,28(4):538-541.SHEN Yang,CHEN Yong-guang,LI Xiu-he.Study on Design andSimulation of Working Mode for Netted Radar Antagonizing AR M[J].Systems Engineering and Electronics,2004,28(4):538-541.(in Chinese)
[3]张光辉,董鹏曙,王震,等.对空情报雷达组网的关键技术与发展构想[J].舰船电子工程,2009,29(12):23-26.ZHANG Guang-hui,DONG Peng-shu,WANG Zhen,et al.Key Technique and Developing Supposition of Air Intelligence Radar Netting[J].Ship Electronic Engineering,2009,29(12):23-26.(in Chinese)
[4]王德纯,丁家会,程望东,等.精密跟踪测量雷达技术[M].北京:电子工业出版社,2006.W ANG De-chun,DING Jia-hui,CHENG Wang-dong,et al.Technique of Precision Tracking Measure Radar[M].Beijing:Publishing House of Electronic Industry,2006.(in Chinese)
[5]Wendong Xiao,Jiankang Wu,Lihua Xie.Adaptive sensor scheduling for target tracking in wireless sensor network[C]//Proceedings of 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings.Singapore:IEEE,2006:705-708.
[6]尹晓锋,姜秋喜,毕大平.雷达侦察系统前端截获概率分析[J].舰船电子工程,2004,24(3):107-109.YIN Xiao-feng,JIANG Qiu-xi,BI Da-ping.Analysis of Radar Reconnaissance System Front Intercept Probability[J].Ship Electronic Engineering,2004,24(3):107-109.(in Chinese)
[7]潘泉.现代目标跟踪与信息融合[M].北京:国防工业出版社,2009.PAN Quan.Modern Target Tracking and Information Fusion[M].Beijing:The National Defense Industry Press,2009.(in Chinese)
[8]Cohen S A.Adaptive variable update rate algorithm for tracking targets with a phased array radar[J].IEEE Communication,Radar and Signal Processing,1986,127(3):277-280.

