LTE系统中基于改进样条插值的信道估计方法❋
李小文,宋海贝,方前军
(重庆邮电大学重庆市移动通信技术重点实验室,重庆400065)
LTE系统中基于改进样条插值的信道估计方法❋
李小文,宋海贝,方前军
(重庆邮电大学重庆市移动通信技术重点实验室,重庆400065)
上行控制信道(PUCCH)格式1/1a/1b在长期演进(LTE)系统中承载重要的控制信令,其信道估计对系统性能有着重要影响。普通循环前缀(CP)时,PUCCH格式1/1a/1b要利用时隙内3个连续排放的导频进行插值需要考虑二阶插值或者三次样条插值。为了使其在TD-LTE测试仪表系统中得到高效实现,分析了两种插值算法,并提出改进的三次样条插值算法,即采用逐步外推的插值思想估计时隙内边缘的数据符号,通过离线完成大部分运算,使得信道估计的实现在减小复杂度的同时还降低了误比特率。
长期演进系统;上行控制信道;信道估计;三次样条插值;DSP实现
1 引言
LTE系统采用了在移动通信技术演进中起主导作用的正交频分复用(OFDM)接入技术,下行采用正交频分多址技术,上行采用单载波频分多址技术(Single Carrier-Frequency Division Multiple Access,SC-FDMA),能够在20 MHz带宽内实现100 Mbit/s的下行峰值速率和50 Mbit/s的上行峰值速率[1]。
经过无线信道的信号通常会经历多径衰落、频率选择性衰落,所以对解调之前的信号进行信道估计在LTE系统中具有重要意义。LTE系统在发送端插入导频,接收端利用导频进行信道估计,通过插值得到整个信道的信道频率响应。信道估计中常用的插值算法有线性插值、二阶插值、三次样条插值、时域插值等,二阶插值的性能优于线性插值[2]。时域插值先将导频的信道频率响应通过IDFT转换至时域,时域补零后再经DFT转换至频域[3],其插值性能高效,但在DSP处理器中实现的难度大。
本文对PUCCH格式1/1a/1b进行基于导频的信道估计,分析了二阶插值、三次样条插值这两种可以应用于若干个连续导频分布的插值算法,推导出实际应用公式,并且提出改进的三次样条插值,即采用逐步外推的插值思想估计一个时隙内边缘的数据符号,充分利用导频的信息对数据符号进行插值。结果表明,改进的插值算法大部分计算都可以离线进行,而且其性能相比于二阶插值、未改进的三次样条插值有明显的提升,适用于TD-LTE测试仪表的实现。
2 PUCCH信道估计
2.1 PUCCH简介
上行控制信道在LTE系统中承载重要的控制信令,在接收端对其进行精确的信道估计对整个系统性能有着重要影响。根据控制信令中包含的信息种类,即上行传输的调度请求(SR)、下行数据包的混合重传请求确认(HARQ ACK/NACK)、信道质量指示器(QI)、秩指示器(RI)、预编码矩阵指示器(PMI),PUCCH支持1/1a/1b、2/2a/2b等几种格式。为了最小化传输控制信令所需要的资源、利用频率分集,PUCCH在一个子帧(subframe)内的资源映射如图1所示。如果同时传输探测参考信号和PUCCH格式1/1a/1b,则PUCCH上最后一个SC-FDMA符号将留给探测参考信号,图1中表示上行配置的带宽,nPRB表示物理资源块的索引号,其中相同m标号的两个资源块(Resource Block,RB)是一个PUCCH域[4]。

图1 PUCCH资源映射Fig.1 Resource mapping of PUCCH
物理上行信道中用于信道估计的导频是解调参考信号(Demodulation Reference Signal,DMRS),它是由通过对Zadoff-Chu序列做循环扩展得到的频域导频序列定义的。
2.2 导频的估计算法
LTE系统在频域的信道估计可以分为估计导频的信道频率响应、数据符号插值两个子模块。基于导频的信道估计有最小二乘(Least Squares,LS)、最小均方误差(Minimum Mean Squares,MMSE)等方法,MMSE比LS性能好,但要求计算信道自相关矩阵,复杂度高[5]。考虑到DSP处理器的性能,本文选用LS算法作为信道估计算法。LS算法就是使平方误差最小,即^Hp=Yp/XP,其中Yp表示接收到的导频,Xp表示本地生成的导频,^Hp表示导频的信道频率响应估计值。
2.3 插值算法
根据DMRS的资源分布,对于扩展CP的PUCCH格式1/1a/1b、普通CP的PUCCH格式2/2a/
2b,其插值均可以采用时隙内线性插值;而对于普通CP的PUCCH格式1/1a/1b,由于其DMRS在每个时隙内是3个连续分布的,所以估计该时隙内数据位置上的信道频率响应不能利用线性插值,可以采用二阶插值或者三次样条插值,两者在MATLAB中存在库函数Lagrangeinterp、spline。但是在DSP处理器中要实现所述插值只能借助于代码,因此DSP实现的关键就是在保证优良性能的条件下尽可能降低复杂度。
2.3.1 二阶插值
已知函数f(l)在3个互异点l0、l1、l2对应的函数值分别为y0、y1、y2,现构造一个插值函数ε(l)=al2+bl+c,使得ε(l)在插值节点li处与f(l)在li处的值相等,即ε(li)=f(li),(i=0,1,2)。
ε(l)的参数a、b、c直接由插值条件决定,即满足下列代数方程组:

由于li互异,故上述方程组系数行列式非零,从而a、b、c是存在且唯一的,利用二阶插值函数的拉格朗日形式构造ε(l)[6]。
令
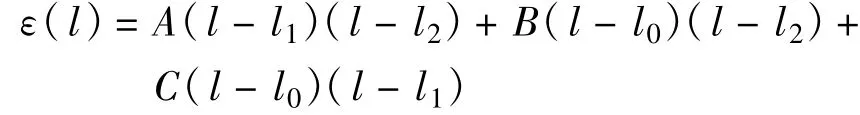
由插值条件ε(l0)=y0,ε(l1)=y1,ε(l2)=y2可以确定待定常数A、B、C,整理得插值函数ε(l)为

2.3.2 三次样条插值
三次样条函数s(l)是一种分段函数,该函数及其一、二阶导数在连接处都是连续的,它在节点li(a=l0<l1<…<ln-1<ln=b)分成的每个小区间[li-1,li](i=1,2,…,n)上是三次多项式,区间[a,b]上共需4n个独立条件确定,由该函数及其一、二阶导数的连续性和插值条件s(li)=f(li),(i=0,1,…,n)可以分别提供3(n-1)、n+1个独立条件,另外两个独立条件可以由两个端点条件决定[7]。由于在信道估计中,待估计信道频率响应的各阶导数未知,所以端点条件设定为

由于s(l)在每个子区间[li-1,li]上为三次多项式,所以样条函数s″(li)在[li-1,li]上是线性函数,记Mi=s″(li),(i=0,1,…,n),则s″(li)在[li-1,li]上可以表示为
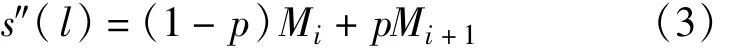
其中p=(l-li)/hi,hi=li+1-li,对式(3)两边进行两次积分,再代入插值节点整理得l∈[li,li+1]时

对式(4)求导可得s′(l),由s′(l)的连续性
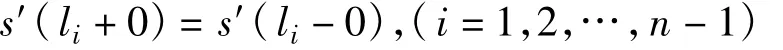
得到Mi(i=0,1,…,n)满足方程组

且
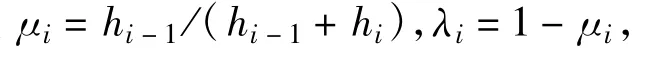

由端点条件式(2)有λ0=μn=1,q0=qn=0,再根据公式(5)、(6)可以得到M0,M1,…,Mn,代入式(4)即得三次样条函数的分段表达式。只要获得插值位置,所述过程大部分都可以离线计算,使其实际应用的复杂度大大降低。
3 改进的三次样条插值算法
对于普通CP的PUCCH格式1/1a/1b,由表2可知,一个时隙内需要进行插值的数据符号数目等于4个(L=0,1,5,6),DMRS的符号数目即插值节点数目等于3个(L=2,3,4),在三次样条插值中相当于l0=2=L2,l1=3=L3,l2=4=L4,对应的函数值f(l)即子载波k上所有DMRS的信道频率响应分别为H(k,L2)、H(k,L3)、H(k,L4)。可见,待插值数据分布于DMRS的两边,不属于任何分段区间,所以相当于在插值区间外作插值运算,进行外插会产生一定的误差,为了减小这种误差,提出一种改进的三次样条插值算法。
改进的三次样条插值算法在所述一个时隙内的操作思想描述如下:
Step1计算数据位置L=1,5处的估计值^H(k,L1)、^H(k,L5):利用子载波k上位置L=2,3,4的所有DMRS的信道频率响应进行三次样条插值,得到区间[L2,L3]、[L3,L4]上的多项式,令与DMRS相邻的数据位置L=1,5分别满足区间[L2,L3]、[L3,L4]上的多项式,按照所述样条插值过程可得估计值^H(k,L1)、^H(k,L5)。
Step2计算数据位置L=0,6处的估计值^H(k,L0)、^H(k,L6):将子载波k上位置L=1,2,3,4,5的符号都看作位置L=0,6用于信道估计的DMRS,根据样条插值原理得到区间[L1,L2]、[L2,L3]、[L3,L4]、[L4,L5]上的多项式,令数据位置L=0,6分别满足两端区间[L1,L2]、[L4,L5]上的多项式,按照所述样条插值过程可得估计值^H(k,L0)、^H(k,L6)。
可见,所述插值算法利用与DMRS相邻的数据位置估计值对边缘位置的数据进行三次样条插值,同时两次利用DMRS的信息,使得符号间信道频率响应的变化更加平滑,估计值更加准确。所述插值过程只描述了PUCCH上3个连续DMRS的情况,实际上改进的样条插值算法适用于3个以上任意多个连续数据的插值运算,可以应用到其它通信系统中,值得推广使用。
4 设计与实现
4.1 DSP处理器
本系统选用TMS320C6455作为开发使用的DSP芯片。该芯片属于高速定点DSP,最高时钟频率为1.2 GHz,16位定点处理性能达9 600 MIPS。
4.2 信道估计的DSP实现
终端所使用的导频是由网络端分配的,在进行信道估计时,网络端将会重新生成本地导频,放置于分配的内存区中。网络端对于上行信道数据的处理以子帧为周期进行,每接收一个子帧的数据就会对其进行A/D转换,然后根据上行信道采用的CP类型进行去CP处理,在FPGA模块完成FFT后传送到DSP处理器。网络端要对从上行信道接收到的数据进行处理,需要区分上行共享信道与上行控制信道,若是PUCCH,再判断具体采用的格式。根据上述获取的信道信息,先将经过FFT处理后的数据进行解资源映射,得到接收的DMRS与数据符号,再将两路数据分别存储。
利用LS算法完成对各天线上DMRS的估计,算法中只涉及到一个除法。由于本地生成的DMRS模值为单位1,所以接收到的DMRS序列与本地生成的DMRS序列的复数相除相当于前者与后者的共轭相乘。为了保证量化精度,需要将相乘结果的实部、虚部的最大值保存,再根据最大值进行归一化操作。
上行信道的DMRS在一个子帧内呈块状分布,在频率方向上都有DMRS符号,所以对数据符号插值只需要在时间方向上进行。利用数据所处的位置可以离线计算三次样条插值的各参数,最后将数据的估计值用DMRS估计值表示出来,并将表示值以数组的形式存放在内存中。设计插值程序为按照时隙内子载波递增的方向进行,即完成一个子载波上的全部数据插值后再对下一个子载波进行操作。
4.3 流程描述
综上所述,PUCCH信道估计的DSP实现主要基于以下6个步骤:
(1)将经FFT处理后的一个子帧数据读取至DSP处理器;
(2)根据高层配置的PUCCH的RB数目、CP类型、格式等参数完成信道类型判断;
(3)将各天线上待处理的数据进行解资源映射,把解得的PUCCH数据及DMRS分别放入分配的内存区;
(4)在接收端生成本地的DMRS,放入分配的内存区;
(5)采用LS算法获得DMRS符号的信道估计值;
(6)读取内存中离线计算的参数,应用改进的三次样条插值估计PUCCH数据符号处的信道频率响应。
4.4 性能分析
在MATLAB仿真环境下对论文所提出的插值算法进行了仿真,并与二阶插值、三次条插值进行了比较。仿真条件选取如下:上行信道是1×2天线的MIMO模型,信道类型是普通CP的PUCCH格式1/1a/1b,带宽为5 MHz,即上行的RB数目是25个,每个子帧只有一个终端,则分配给PUCCH的RB数目是1个,FFT大小是2 048,并且不同时传输探测参考信号。
图3给出了各种插值算法在扩展步行A(Extended Pedestrian A,EPA)、多普勒频移5 Hz信道条件下的仿真性能。对比基于LS信道估计的二阶插值、三次样条插值以及改进的样条插值算法可知,由于改进的样条插值算法两次利用DMRS的信息,比前两者的插值都更为可靠,其误比特率明显最低,所以性能最优。

图2 EPA 5 Hz信道估计的插值算法性能对比Fig.2 Performance comparison of interpolation algorithms in EPA with 5 Hz
在DSP处理器的软件实现中,通过优化程序循环体、指令并行,充分利用程序中的“NOP”指令[8],按照上述仿真条件设计程序,经过程序运行,可以得到采用改进的三次样条插值进行信道估计时主要模块的最大执行周期数目(Cycle)数目,如表1所示。

模块 周期/cycle DMRS产生 58 000×2解资源映射 5 100×2 LS估计 2 600×2改进的样条插值 1 800×2总和135 000
TMS320C6455芯片的最高时钟频率为1.2 GHz,即在一个子帧的1 ms时间内可以完成1.2×106cycle的计算,本文方案的主要模块只需要1.35×105cycle,完全可以满足系统实时处理的需要。由于二阶插值、三次样条插值以及改进的样条插值大部分的计算都可以离线进行,三者在不同数据位置处的估计值都可以用DMRS的信道频率响应表示出来,所以在DSP实现的复杂度都是相当低的,具有高效的实时处理能力,但是改进的样条插值性能是最优的。
通过以上分析可知,改进算法不仅保证了插值计算的低复杂度,还降低了误比特率,因此非常适合TD-LTE系统的要求,可以应用于该系统的实现。
5 结束语
LTE系统要求提供速率更高的数据业务,因此对系统的实时性要求也更高。本文介绍了LTE上行控制信道的承载内容及映射方式,对现有的信道估计插值算法进行了详细分析,提出了一种基于DSP的PUCCH格式1/1a/1b信道估计插值模块的实现方案。通过分析其实现复杂度以及定点运算性能表明,该方案可以满足实时处理的要求,在保证低实时处理复杂度的条件下,其信道估计性能得到明显提升,对LTE系统物理层的软件开发工作具有重要的意义,同时也为其它通信系统提供了一种插值实现方案,值得推广使用。
[1] Stefania Sesia,Issam Toufik,Matthew Baker.LTE-The UMTS长期演进理论与实践[M].马霓,邬刚,张晓博,等,译.北京:人民邮电出版社,2009:5-11.
Stefania Sesia,Issam Toufik,Matthew Baker.LTE-The UMTS Long Term Evolution From Theory to Practice[M].Translated by MA Ni,WU Gang,ZHANG Xiao-bo,et al.Beijing:People′s Posts&Telecom Press,2009:5-11.(in Chinese)
[2] Meng-Han Hsieh,Che-Ho Wei.Channel estimation for OFDM systems based on comb-type pilot arrangement in frequency selective fading channels[J].IEEE Transactions on Consumer Electronic,1998,44(1):217-225.
[3]陈奎,徐钊.OFDM系统二维变换域信道估计算法[J].电子科技大学学报,2009,38(6):927-931.
CHEN Kui,XU Zhao.2-D Transform Domain Channel Estimation Method for OFDM Systems[J].Journal of University of Electronic Science and Technology of China,2009,38(6):927-931.(in Chinese)
[4] 3GPP TS 36.211 v9.0.0,Evolved Universal Terrestrial Radio Access(E-UTRA)Physical Channels and Modulation(Release 9)[S].
[5] Sinem Coleri,Mustafa Ergen,Anuj Puri,et al.Channel Estimation Techniques Based on Pilot Arrangement in OFDM Systems[J].IEEE Transactions on Broadcasting,2002,48(3):223-229.
[6]李岳生,黄友谦.数值逼近[M].青岛:人民教育出版社,1978:27-30.
LI Yue-sheng,HUANG You-qian.Numerical Approximation[M].Qingdao:People′s Education Press,1978:27-30.(in Chinese)
[7]程正兴,李水根.数值逼近与常微分方程数值解[M].西安:西安交通大学出版社,2000:67-75.
CHENG Zheng-xing,LI Shui-gen.Numerical Approximation and Numerical Solution of Ordinary Differential Equations[M].Xi′an:Xi′an Jiaotong University Press,2000:67-75.(in Chinese)
[8] Texas Instruments Incorporated.TMS320C6000系列DSP编程工具与指南[M].田黎育,何佩琨,朱梦宇,译.北京:清华大学出版社,2006:32-50.
Texas Instruments Incorporated.TMS320C6000 series DSP programming tools and guidelines[M].Translated by TIAN Li-yu,HE Pei-kun,ZHU Meng-yu.Beijing:Tsinghua University Press,2006:32-50.(in Chinese)
LI Xiao-wen was born in Chongqing,in 1955.He received the M.S.degree in signals and systems from Chongqing University in 1988.He is now an instructor of graduate students.His research concerns TD-LTE development of integrated test instruments.
宋海贝(1987-),女,河南鹤壁人,2009年获河南师范大学电子信息工程专业工学学士学位,现为硕士研究生,主要研究方向为LTE系统物理层关键技术;
SONG Hai-bei was born in Hebi,Henan Province,in 1987. She received the B.S.degree in Electronic and Information Engineering from Henan Normal University,in 2009.She is now a graduate student.Her research concerns LTE system physical crucial technology.
Email:songhaibei1987@163.com
方前军(1985-),男,湖北荆州人,2009年获工学学士学位,现为硕士研究生,主要研究方向为LTE系统物理层关键技术。
FANG Qian-jun was born in Jingzhou,Hubei Province,in 1985.He received the B.S.degree in 2009.He is now a graduate student.His research concerns LTE system physical crucial technology.
A Channel Estimation Algorithm Based on Improved Spline Interpolation in LTE Systems
LI Xiao-wen,SONG Hai-bei,FANG Qian-jun
(Chongqing Key Lab of Mobile Communicatins,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
In the Long Term Evolution(LTE)system,the physical uplink control channel(PUCCH)format 1/1a/1b carries important control information,channel estimation of which has great impact on the system performance.In the condition of normal cyclic prefix(CP),the second order or spline interpolation should be considered for PUCCH format 1/1a/1b to exploit three continuous pilots in one slot.To implement it efficiently in the TD-LTE test system,two interpolation algorithms are analysed and a better algorithm based on spline is proposed.The thought of stepwise extrapolation is adopted in the algorithm to estimate the data at the edge of the slot,and most of the computations are performed offline resulting in high performance at complexity reductions.
LTE system;physical uplink control channel;spline interpolation;channel estimation;DSP implementation
The National Science&Technology Major Project(2009ZX03002-009)
TN929.5
A
10.3969/j.issn.1001-893x.2011.04.023
李小文(1955-),男,重庆人,1988年获重庆大学信号与系统专业工学硕士学位,现为重庆邮电大学硕士生导师,主要从事TD-LTE综合测试仪表的开发;
1001-893X(2011)04-0106-05
2011-01-10;
2011-03-02
国家科技重大专项项目(2009ZX03002-009)

