航天测量船外测数据异常值自适应处理算法设计❋
李辉芬,周锦标,何剑伟,李晓勇,陈红英
(中国卫星海上测控部,江苏江阴214431)
航天测量船外测数据异常值自适应处理算法设计❋
李辉芬,周锦标,何剑伟,李晓勇,陈红英
(中国卫星海上测控部,江苏江阴214431)
航天测量船外测数据中蕴含有复杂的变形和船摇周期,增加了数据检择难度。针对船测数据特性,对多种辨识方法的检择效果进行了专题研究,结合滑动中值平滑估计模型,构建了参数自适应信息检择算法,利用周期图方法实现了平滑区间的动态调整,解决了测量船外测数据的纠错难题。
航天测量船;外侧数据;数据特性;异常值;自适应处理
1 引言
测量数据中,严重偏离大部分数据所呈现趋势的小部分数据点被称为异常值或野值。异常值的辨识和处理是数据处理工作的重要一环,它是提高处理精度、改善处理结果质量的有效措施。航天测量船上的外测设备其基座直接固连于船体甲板上,而测量船是一个运动的平台,在海上测量时是在动态条件下进行的,船的位置和姿态在不断地变化,其外弹道测量获取的测量数据中除含有跟踪测量设备本身的测量误差外,还叠加了船体姿态(即基座姿态)的测量误差,在观测序列中蕴含有复杂的船摇周期[1],给异常值的辨识工作带来了难度。为了解决包含有复杂变形、船摇周期的测量船外测数据的纠错难题,我们针对测量船数据特性,对多种辨识方法的处理效果(以下称为检择效果)进行了专题研究。
2 船摇数据特性分析
船载测量设备对飞行目标实施测量时,由于船舶摇摆,在测量数据中迭加了船摇信息,使原始测量数据带有明显的船摇数据特性,本应比较平滑的曲线变得像船摇数据那样带有周期性的起伏,船摇对测量元素R、E、A都有影响,尤其对测角元素E、A的影响更加明显。航天测量船有一套复杂的计算方法和公式完成船摇修正,除去船载外测数据中船摇造成的影响,恢复外测数据原来的特性(就像陆上测量一样),这项工作在由测量坐标系转换到测量船惯导地平系的过程中完成。但在航天发射任务中测量船原始测量数据的检择工作在测量坐标系就要进行,数据中蕴含的复杂船摇周期,给异常值的识别工作带来了难度。从测量船跟踪ERS2卫星的测量系俯仰角数据曲线(图1)可以明显地看到,由于船摇的影响,数据曲线是一种非单调变化的数据序列。

图1 测量船跟踪ERS2卫星俯仰角曲线图Fig.1 Curve of elevation angles when a space tracking ship is tracking ERS2 satellite
船摇数据反映了船摇的客观现实,研究船摇数据特性,了解船摇的运动规律,对于寻找一种既能提取有效信息、滤去误差数据,又不破坏数据本身所隐含的船摇周期的检择算法是有帮助的。对船摇运动规律的认识,有助于进一步了解船载设备测量数据特性,建立符合船摇运动客观规律的数据处理模型。我们从艏摇(即航向)、纵摇、横摇3个方向来考虑船体的摇摆运动,在这3个方向它具有不同的特征表现。在航天测量船船摇数据中,隐含着一些规律性的东西,如船摇周期。确定船摇数据所隐含的周期,对建立适用于测量船数据特性的检择模型是有帮助的。
设船摇测量数据xi的数学模型为

式中,{εi}是独立于{ai,bi}的随机过程,E(εi)=0,
采用周期图方法搜索船摇数据中隐含周期{fi}的基本思想:假定f1的估计为,则可由求和。若和f1相差甚远或者说模型中没有该频率,则所估计的系数实际上不存在,那么必近似为零。用一组足够密的频率作试探并绘出模平方()对的图形,则当和{fi}中某一值接近时,()将异于零,否则近似为零。那么根据平方模的值足够大处所对应的f便可判断其频率及其相应的振幅[2]。在fi已知的情况下,的估计由下式给出:

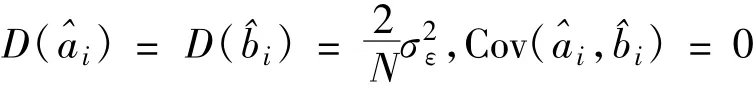
N个观测值x1,x2,…,xN的周期图定义为
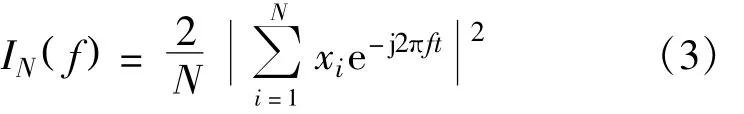
实际计算中IN() f的频率取值是离散的,一般取,公式(3)在f处展开p后可写成:

由此可见,当fp的值等于xi中所含周期的频率时有,周期图有较大的峰值。航天测量船的船摇周期,除了与船体性能有关外,还与海况和测量船的航行工况有关。由于船体的摇摆运动在船的不同方向上具有不同的特征表现,分别对航天测量船的艏摇(航向)、纵摇、横摇3个方向的数据进行分析研究,寻找各自隐含的周期。用上述方法处理航天测量船100 s实测船摇数据(采样间隔0.05 s,共2 000点,N=2 000),绘制3个方向(艏摇、纵摇、横摇)的周期图(见图2)。从艏摇数据的周期图看,INf()p在p=1时有明显峰值,可得到该组数据的周期T=2 000/(1×20)=100 s,该组数据从整体上看不具有明显的周期性;对于纵摇数据的周期图,峰值在p=12处达到,其周期为T=2 000/(12×20)=8.3 s;对于横摇数据的周期图,有一个明显的峰值在p=8处达到,故其相应的周期为T=2 000/(8×20)=12.5 s。与实测数据特性比较,用周期图方法得到的结果与实际情况是吻合的,该次任务艏摇没有明显的周期性,纵摇和横摇则有10 s左右的基频存在,且纵摇的周期略小于横摇周期,船摇数据中含有一个与时间无关而与船摇角度有关的周期误差[3],用周期图方法搜寻数据中隐含的周期规律是行之有效的。

图2 船摇数据航向角、纵摇角、横摇角周期图Fig.2 Periodogram of yaw angles,pitch angles androll angles of a space tracking ship
船体不同方向的摇摆变化对R、E、A的影响也是不同的,纵、横摇的影响比较复杂,不仅与当前的测量值有关,还受设备跟踪性能、测量工况的影响。相比之下,航向的影响比较简单,主要影响方位。横摇对距离的影响最明显,俯仰角则同时受纵、横摇的影响,3个方向的船摇数据对方位角均有影响,但航向对方位角的影响最大[1]。变形对距离基本没有影响,但对角度的影响却很明显。
3 航天测量船异常数据检择算法设计
测量船观测数据序列中出现的野值点通常分为下列两种类形:
(1)单个野值:也称孤立型野值。特征是某一采样时刻ti处测量数据是否为野值,与ti-1及ti+1时刻数据的质量无必然联系,而且,比较常见的情况是当ti时刻的测量数据异常时,在ti时刻的邻域内{ti-k,…,ti-1,ti+1,…,ti+k}的测量数据质量是好的,即野值点的出现是孤立的。
(2)成片野值:也称野值斑点,简称斑点。基本特征是在某时刻ti出现野值,可能带动相邻时刻数据{y( ti+1),…,y( ti+p)}均严重偏离测量数据真值,即野值点会成片出现。船载设备在高仰角跟踪目标时的测量数据中,野值斑点的出现是较为常见的现象。
各类野值在观测数据序列中通常以下列形式出现:
(1)重复性异常:在测量数据序列中,异常数据按某一规律周期性地或非周期性地重复出现。这种异常多半是由于设备故障产生的,有时也可能是由于习惯性的人为操作错误而产生。
(2)固定性异常:在测量数据序列中,存在大小基本不变的很大的固定误差,这可能是因为设备故障、操作错误、用错常数所致。
(3)随机性的异常:出现的时间、幅值大小都是随机变化的,多因设备工作不稳定或受到随机干扰而产生。
飞行试验中导致异常数据发生的原因是多方面的、随机的,非常复杂。设备工作不正常、某些部件发生故障、设备未调整到最佳工作状态、环境条件变化、电源不稳定、人为操作错误等致使设备在测量、记录或传输过程中出现异常[4],还有数据处理中出现的差错、比较标准数据本身的错误等都会导致异常数据的出现。两种或两种以上类型的异常数据常常会混合出现。异常数据如果不予以分离和消除,将给数据处理带来误差,影响计算结果的正确性[5],降低观测数据的置信度,因此,要保证数据处理结果的质量,必须判别和处理观测数据中的异常值,以合理、可信的数据替代它。
异常数据的检验方法种类繁多,有试验场常用的外推拟合方法,以及多项式回归模型检验法、自回归求和滑动平均模型(ARIMA模型)检验法、t-检验法、偏度-峰度检验法、极差检验法和M估计技术等多种方法。由于异常数据产生的原因各不相同,很难找出一种通用的方法来解决。对不同类型的异常数据需采用不同的辨识方法。静态测量数据的异常值比较容易判别,对飞行试验中的异常数据,即对动态测量数据中的异常值,缺少高效率的辨识方法。航天测量船通常采用直观法、统计法和纵横比较法3类方法完成异常数据的辨识[6]。
常用的直观方法有观察法、标图法和差分法。差分法可以直观、明了地反映出数据的异常现象,适用于误差与真值没有分离的情况。差分检择算法用于判别孤立型异常值时效果是好的,但对于斑点型异常数据的处理就比较困难了,容易出现误判和漏判现象。
用统计检验的方法来辨识异常数据,主要是根据小概率原理和测量误差服从正态分布的假设。统计方法作出的判断较为严格,但方法繁琐,而且统计方法都假定了误差服从正态分布,且都要用到误差数据的统计方差,因此,必须满足随机误差是平稳的这个条件。实际情况很难与理论条件完全一致,测量对象本身也很难用某种形式的多项式来拟合。
纵横比较法是将某设备的测量数据与跟踪同一目标的其它设备的测量数据比,或与标准数据比,或与历史资料比,通过比较对应参数(如坐标与速度、速度与加速度等)之间的协调性,特别是考察参数曲线的极值点、拐点等对应关系,来检查时间关系是否正确、数据间的匹配关系是否正常、是否有野值存在等异常情况。在海上精度校飞时,通过比较不同架次、不同进入之间的误差曲线,也能发现异常。如测量船海上校飞,我们利用GPS数据完成异常数据的辨识工作,该方法利用GPS数据作为标准数据得到比对残差,构造“数据管道”,可以很好地纠正和抑制残差序列中超差数据的比例,提高参与综合处理的有效数据量,但缺点是要求比对标准质量可靠,不能包含异常数据。而海上测量常受复杂海况的影响,GPS数据也常常出现异常,在一定程度上制约了该方法的使用效果。所以,最好能找到一种方法,不需要简单地按某一人为门限舍去异常值,而是设法减小异常数据的影响,这对于数据处理工作来说,更有实用价值。我们知道,中值是均值的最稳健估计,其小样本崩溃点接近50%,采样数据集的任一非空子集中当野值点的个数不足一半时算法都不会崩溃[7]。对此,我们引入了基于中值估计的容错平滑器,来设计适用于测量船数据特性的信息检择算法。
参数自适应信息检择算法是为解决航天测量船包含有复杂变形、船摇周期的外测数据的纠错难题而设计的,它结合周期图方法,选用文献[7]提出的“滑动中值平滑估计模型”构建的信息检择算法。假定采样数据序列为yi(i=1,2,3,…,n),滑动中值平滑估计模型定义如下[7]:

式中,y(j)表示对{y1,y2,…,ym}按从小到大排序后的第j个数值,med{·}为中值算子:

航天测量船数据序列中蕴含有船摇周期,采用的检择算法既要能滤去误差数据,同时又不破坏数据本身隐含的船摇周期的变化规律,因此,中值和均值平滑区间的准确设置是非常关键的,区间设置太小,不能滤去误差数据,设置太大,又会破坏正常的船摇周期。基于此要求,我们将周期图方法引入到中值容错平滑算法中,根据异常数据长度及所处区域船摇周期变化情况,实现了滑动中值平滑区间及局部均值平滑区间参数的动态调整,来适应测量船这种蕴含有船摇周期非单调变化数据的特点,并将算法改进如下:
步骤1:利用周期图方法搜寻该组数据蕴含的船摇周期,确定参数m、s、p的初值。
步骤2:设置参数k=m,用滑动中值平滑器构造滑动中值平滑序列{^yi|m|i=1,2,3,…}。
步骤3:设置参数k=s,用滑动中值平滑器对平滑序列{^yi|m|i=1,2,3,…}进行第二次中值平滑,

步骤5:为补偿中值均值平滑对采样数据列中趋势性分量的不利影响,构造过程信号的中值-均值平滑残差序列:

步骤6:对残差序列{Δyi|i=1,2,3,…},重复步骤1~3,得到残差序列的滑动中值-均值平滑估计:
步骤7:计算序列{yi|i=1,2,3,…}的平滑结果:
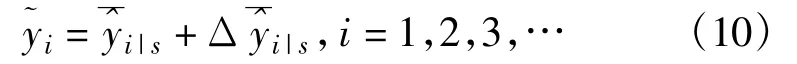
步骤8:以平滑估计值˜yi为比对标准数据构造残差序列:

步骤9:数据诊断。构造检择函数

式中,c为检测门限。
将野值点检择问题转化为0/1序列。R(x)为1时,数据正常;R(x)为0时,标识为异常数据。当0成串出现时所对应的多个野值点即为斑点,需要修复。
步骤10:数据修复。利用周期图方法搜索野值斑点所处区域的船摇周期,结合斑点长度,调整参数m、s、p,重复步骤2~7,完成该区域异常数据的修复。
该算法对含有时变趋势分量或均值非平稳的采样时间序列的平滑效果好,它采用分阶段多次滑动中值与滑动均值平滑组合,得到中值平滑估计值,并构造过程信号的中值-均值平滑残差序列来补偿中值平滑对采样数据列中趋势性分量的不利影响。
4 纠错效果分析
我们用测量船跟踪ERS2卫星的数据来检验参数自适应信息检择算法的纠错效果,发现无论是趋势性变化的数据列,还是周期性变化的数据列,采用自适应信息检择算法都能可靠地从带斑点型异常值的采样数据序列中无偏地提取信息,有效地检择出数据列中的野值,替代数据也符合数据的变化趋势,纠错效果好。参数自适应信息检择算法是一种稳健的中值估计方法,它采用分阶段多次滑动中值与滑动均值平滑组合,得到中值平滑估计值3,…}。为补偿中值平滑对采样数据列中趋势性分量的不利影响,还通过构造过程信号的中值-均值平滑残差估计{Δ1,2,3,…}来补偿1,2,3,…}。从船 跟踪ERS2卫星的测量系俯仰角数据曲线可以明显地看到(见图1),由于船摇的影响,俯仰角数据曲线是一种非单调变化的数据序列,数据中多处存在斑点型野值(见表1)。

表1 纠错前后俯仰角数据随机误差统计表Table 1 Random errors of elevation angles before and after error correction
应用参数自适应信息检择算法对测量系数据进行纠错,虽然数据序列中蕴藏着船摇周期,但纠错效果理想。将纠错后的数据修正船摇误差后转地平系,数据的变化趋势正常,各野值区域既滤去了误差数据,又未破坏数据本身隐含的船摇周期的变化规律,说明该方法适用于蕴含有船摇周期的非单调增减数据的纠错工作。
5 结束语
异常数据的纠错处理是提高处理精度、改善处理结果质量的有效措施。我们从航天测量船数据处理工作的实际需要出发,以“中位数容错平滑器”为核心,结合周期图方法,设计了参数自适应信息检择算法,解决了测量船外测数据的纠错难题。在“神舟”飞船任务中,用该算法成功地解决了航天测量船第41、45圈外测数据严重跳变的问题,使有效测量数据延长了60 s。用该算法对测量船第一圈抖动严重的某外测设备俯仰角数据进行纠错处理后,初轨计算中轨道半长轴的外符合精度提高了3倍。
[1]李辉芬,朱伟康,周朝猛,等.船载USB瞬时站址残差异常情况分析[J].电讯技术,2010,50(2):57-62.
LI Hui-fen,ZHU Wei-kang,ZHOU Chao-meng,et al. Exceptional Phenomenon Analysis of Instrumentation Ship’s USB Residual Error[J].Telecommunication Engineering,2010,50(2):57-62.(in Chinese)
[2]张忠华,李晓勇,杨磊,等.航天测量船船姿数据处理方法[M].北京:国防工业出版社,2009.
ZHANG Zhong-hua,LI Xiao-yong,YANG Lei,et al.Ship attitude data processing methods applied to space tracking ships[M].Beijing:National Defense Industry Press,2009.(in Chinese)
[3]李晓勇,张忠华,张同双,等.航天测量船船摇数据特性分析[J].中国惯性技术学报,2006,14(3):27-30,41.
LI Xiao-yong,ZHANG Zhong-hua,ZHANG Tongshuang,et al.Characteristics analysis on spacecraft TT&C ship swaying data[J].Journal of Chinese Inertial Technology,2006,14(3):27-30,41.(in Chinese)
[4]茅永兴,张忠华,章剑,等.单通道相参测控体制下多站触发对测距性能的影响[J].电讯技术,2009,49(4):89-93.
MAO Yong-xing,ZHANG Zhong-hua,ZHANG Jian,et al. Exceptional Phenomenon Analysis of Instrumentation Ship′s USB Residual Error[J].Telecommunication Engineering,2010,50(2):57-62.(in Chinese)
[5]康德勇,李晓勇,王旭良.船位误差对外弹道测量及定轨精度的影响[J].电讯技术,2010,50(9):106-109.
KANG De-yong,LI Xiao-yong,WANG Xu-liang.Influence of Ship′s Position Error on Exterior Trajectory Measurement and Orbit Determination[J].Telecommunication Engineering,2010,50(9):106-109.(in Chinese)
[6]李辉芬,张忠华,朱伟康.船载设备测量数据处理结果的综合分析方法[J].飞行器测控学报,2008,27(6):65-70.
LI Hui-fen,ZHANG Zhong-hua,ZHU Wei-kang.The Exterior Tracking&Measuring Data Analyzing and Processing of Instrumentation Ship[J].Journal of Spacecraft TT&C Technology,2008,27(6):65-70.(in Chinese)
[7]胡绍林,许爱华,郭小红.脉冲雷达跟踪测量数据处理技术[M].北京:国防工业出版社,2007. HU Shao-lin,XU Ai-hua,GUO Xiao-hong.Data processing technology applied to pulse radar tracking[M].Beijing:National Defense Industry Press,2007.(in Chinese)
LI Hui-fen was born in Zhaotong,Yunan Province,in 1968.She is now a senior engineer with the M.S.degree.Her research concerns maritime measurement data processing and precision analysis.
Email:wylhf@yeah.net
周锦标(1966-),男,江苏人,高级工程师,长期从事航天测控总体工作;
ZHOU Jin-biao was born in Jiangsu Province,in 1966.He is now a senior engineer.His research concerns space tracking management.
何剑伟(1967-),男,江苏人,高级工程师,长期从事海上测控软件总体工作;
HE Jian-wei was born in Jiangsu Province,in 1967.He is now a senior engineer.His research concerns space tracking software development.
李晓勇(1963-),男,湖南人,高级工程师,长期从事数据处理与精度分析工作;
LI Xiao-yong was born in Hunan Province,in 1963.He is now a senior engineer.His research concerns data processing and precision analysis.
陈红英(1983-),女,四川人,工程师,长期从事数据处理工作。
CHEN Hong-ying was born in Sichuan Province,in 1983. She is now an engineer.Her research concerns data processing.
Adaptive Processing of abnormal Value in Measured Data by Space Tracking Ship
LI Hui-fen,ZHOU Jin-biao,HE Jian-wei,LI Xiao-yong,CHEN Hong-ying
(China Satellite Maritime Tracking and Controlling Department,Jiangyin 214431,China)
The measured data by space tracking ship contain complicated ship deformation and ship-swaying period,which cases the difficulty to process the abnormal values.According to the data characteristics of ship,a specific study is performed on the selection results of several identification methods.With moving median smoothing estimation model,an adaptive processing method for measured data is designed.Dynamic adjustment between smoothing intervals is implemented by applying periodogram analysis,thus accomplishing the error correction of measured data by tracking ship.
space tracking ship;measurement data;data characteristics;abnormal value;adaptive processing
TN911;TP274
A
10.3969/j.issn.1001-893x.2011.04.012
李辉芬(1968-),女,云南昭通人,硕士,高级工程师,主要研究方向为海上测量数据处理与精度分析工作;
1001-893X(2011)04-0054-06
2011-01-30;
2011-04-11

