直流调速系统PID参数动态设计方法及应用

李 力 余新亮 李 骥

(1.三峡大学水电机械设备设计与维护湖北省重点实验室,湖北宜昌 443002;2.三峡大学机械与材料学院,湖北宜昌 443002)

在龙门刨床、可逆轧钢机、造纸、印染设备等领域中,直流调速系统有广泛的应用[1].一般该系统由内、外双调节环组成,即电流环和转速环,电流环的作用是控制系统电流,转速环的作用是调节系统转速,二者均采用闭环结构,因此,双闭环直流调速系统动静态特性好,抗干扰能力强,平滑调速性能范围宽.实际应用中系统转速环和电流环均采用PID调节器控制,调节器参数的设计主要有经典设计法和常规参数整定法[2],但这些方法主要是基于对象已定,或将对象模型认为是固定不变加以考虑的,难以适应复杂过程的控制,参数的在线调整,也容易忽略影响系统性能的一些其他关键因素,造成系统性能难以精确达到设计指标,设计过程存在着一定的复杂性.因此,本文针对这一问题开展了工作,对调节器参数设计方法进行了改进,探索了一种动态参数设计方法的应用[3-4],实现了系统性能指标精确性设计.

1 经典双闭环直流调速系统

图1所示为经典双闭环直流调速系统[5].系统设置两个调节器ACR和ASR分别调节电流和转速,具体调节过程如下.

图1 双闭环直流调速系统原理

当电动机启动,加速后,转速 n上升到给定值n*,由于电流、转速双闭环反馈控制,因此此时ASR调节器的转速偏差电压Δ Un为零,即

式中,n为实际转速;n*为给定转速;Un为反馈电压;为给定电压;Δ Un为转速偏差电压.同时此时系统电枢电流Id和负载电流IdL关系满足:

因此电动机将会继续加速,使转速n超过了给定值n*,造成转速偏差电压Δ Un＜0,即

由于Δ Un＜0,ASR调节器调节使电流反馈Ui和电枢电流Id下降,但此时电枢电流和负载电流仍满足式(2),转速仍在上升,直至二者相等,转速达到最大值nmax,即

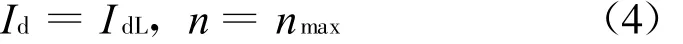
此后,负载的作用迫使电动机开始减速,相应也会出现Id＜IdL一段的过程,转速由加速变为减速,直到稳定.在上述调节过程中,ACR调节器力图使电枢电流Id尽快跟随给定值,以保持电动机转速恒定.

可见,转速调节器ASR和电流调节器ACR在双闭环直流调速系统的控制中有着不可替代的作用.而对于ASR、ACR调节器本身来说,其主要是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的,相应地根据被控过程的特性,可以确定调节器的比例系数KP、积分时间系数KI和微分时间系数KD,三者也由此构成了PID调节器参数的核心.

在PID控制中[6],当比例(P)增大,系统响应快,对提高稳态精度有益,但过大易引起过度的振荡,降低相对稳定性;微分(D)对改善动态性能和抑制超调有利,但过强,即校正装置的零点靠近原点或者使开环的截止频率增大,不仅不能改善动态性能,反而易引入噪声干扰;积分(I)的作用主要是消除或减弱稳态误差,但会延长调整时间,参数调整不当会容易振荡.经典设计方法是利用“最佳”参数计算公式通过反复试凑以确定调节器的特性,这样使得经典设计方法存在以下缺陷.

(1)利用“最佳”参数计算公式设计系统时,如果系统性能不够满意,不能明确调整参数的方向,设计过程繁琐.

(2)设计过程对实际系统进行了简化处理完全忽略了非主导极点及闭环零点对系统性能的影响,而且不能考虑到调节器饱和等关键问题,使得计算结果存在误差.

(3)对于复杂的不可能简化成典型系统的情况及有高精度性能指标要求的情况,利用经典设计方法有一定的困难.因此,有必要对经典设计方法做出改进,克服上述方法的不足.

2 动态参数设计方法原理与应用

2.1 动态仿真模型建立

由图1双闭环直流调速系统的原理可知,考虑工程设计的一般原则,忽略反馈电动势,可得相应双闭环直流调速系统动态结构框图,如图2所示.利用Matlab的单输入单输出系统设计工具(SISO Design T ool),结合双闭环直流调速系统动态结构框图,建立双闭环控制模型,如图3所示.

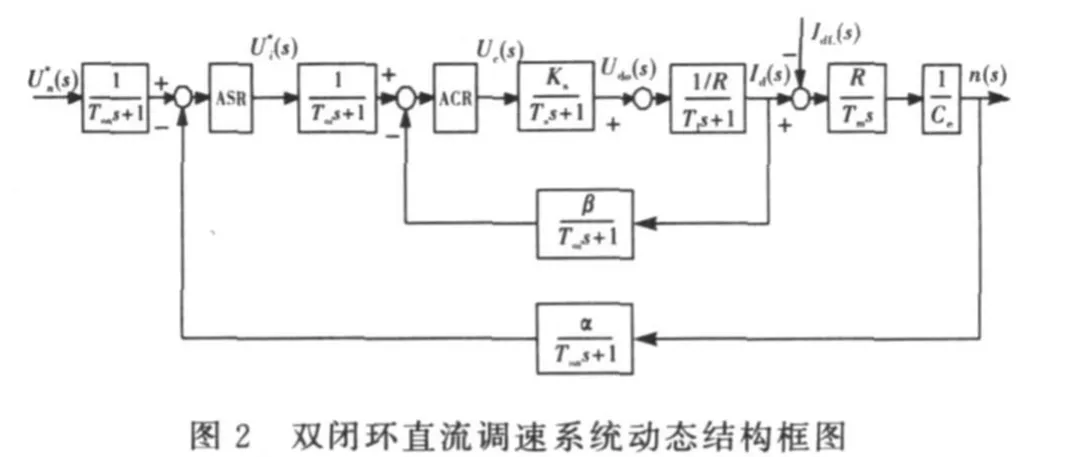
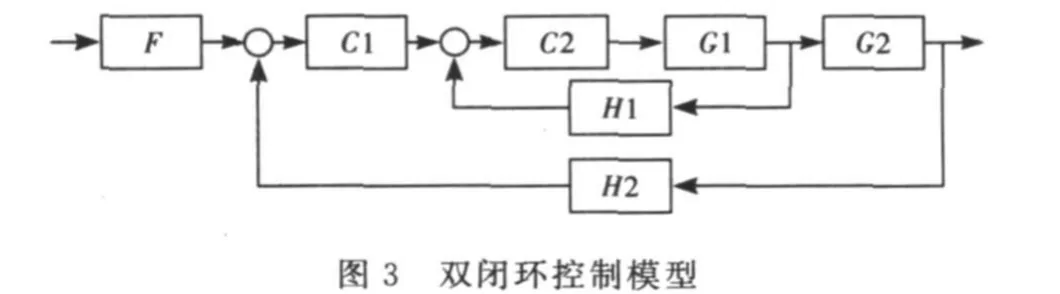
并定义各个模块传递函数:

式中,KPn为ASR调节器的比列放大系数;KIn为ASR调节器的积分时间系数;KDn为ASR调节器的微分时间系数;KPi为ACR调节器的比列放大系数; KIi为ACR调节器的积分时间系数;KDi为ACR调节器的微分时间系数;Ks为晶闸管装置放大系数;R为电枢回路总电阻;Ce为电动机时间常数;Toi为电流滤波时间常数;Ton为转速滤波时间常数;Tm为机电时间常数;Tl为电枢回路电磁时间常数;Ts为电力电子变换器滞后时间常数;α为转速反馈系数;β为电流反馈系数.

这样就建立了双闭环直流调速系统动态仿真模型,为PID调节器参数动态设计提供了基础.

2.2 动态参数设计方法原理

动态仿真模型构建后,根据现有双闭环直流调速系统参数,得出各个模块的传递函数,并将其导入仿真模型工作空间,将会自动生成双闭环直流调速系统的根轨迹图、伯德图,同时交互输出系统性能指标.设计PID调节器参数时,动态调整根轨迹图中相关零点和极点的配置,并实时分析系统的性能指标.经过多次有规律地动态调节设计,分析调整实时交互的系统性能指标,最终可以使系统性能指标精确达到设计要求.由此,建立动态仿真模型,将动态参数设计方法应用于PID调节器设计,不仅能够满足系统性能指标的要求,而且在精确性方面也有极大的改善,显然优于经典设计方法.

2.3 应用实例

选择某晶闸管供电的双闭环直流调速系统,基本参数为:直流电动机:220 V,136A,1460r/min,Ce= 0.132V◦min/r;主轴飞轮惯量GD2=22.5N◦m2;晶闸管装置放大系数Ks=40;电枢回路总电阻R= 0.5 Ω,总电感L=15mH;时间常数Ts=0.016 7 s, Tl=0.03 s,Tm=0.002 s,转速反馈系数α=0.007 V◦min/r,电流反馈系数β=0.05V/A;滤波时间常数Tei=0.002 s,Ton=0.01s.系统设计要求为:转速超调量σ≤16.2%.

根据前述定义,得各模块相应传递函数:

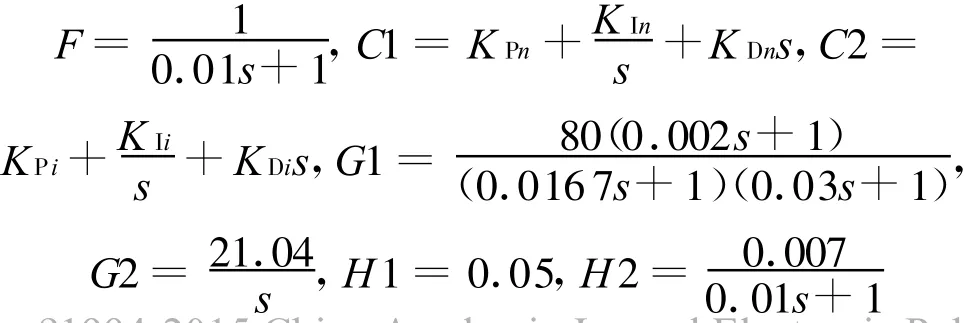
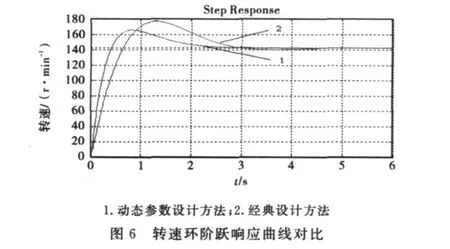
代入仿真模型进行分析,动态设计PID控制器参数,即在系统的根轨迹图上添加一个位于原点处的极点和一对共轭零点,同时观测系统性能指标,精确调整零点和极点的位置,以达到系统性能指标的要求.经过多次动态参数设计优化,得到较优的电流环和转速环的伯德图、根轨迹图,如图4所示,阶跃响应曲线如图5和图6所示.

2.4 比较分析

采用经典设计方法,其电流环和转速环阶跃响应曲线如图5和图6所示.对比动态参数设计与经典设计系统性能指标结果(见表1),不难看出应用动态参数设计方法,电流环和转速环的阶跃响应曲线明显发生了变化,系统整体性能指标有所改善,且优于经典设计方法结果,也完全满足设计要求,说明动态参数设计优于经典设计方法.

表1 动态参数设计与经典设计方法系统性能指标结果比较

3 结 论

针对经典设计方法的缺陷,提出了动态参数设计方法,建立双闭环直流调速系统的动态仿真模型,通过应用实例分析,主要结论如下:

(1)建立动态仿真模型,运用动态参数设计方法,实时交互仿真结果并进行动态调整,实现了系统性能精确性设计,利于设计出高精度系统.

(2)在动态参数设计时,要注意以下规律:①适当添加零点并合理配置极点的位置,有意识地在系统中适当添加零点,可以改善系统的动态过程,抵消影响系统动态性能不利的极点,配置的极点应尽量表达到满足系统设计要求的希望区域;②动态调节的过程中要根据交互仿真结果,实时作出分析,确定参数调整的方向,减小调整的盲目性.

(3)仿真实验结果表明,与经典设计方法相比,动态参数方法具有良好的设计可行性和精确性,运用于双闭环直流调速系统PID调节器参数设计有一定的优越性.

[1] 陈 群.双闭环直流调速系统及其动态仿真[J].科技情报开发与经济2007,17(22):162-163.

[2] 李瑞霞.智能PID整定方法的仿真与实验研究[D].太原:太原理工大学,2007.

[3] Zhuang Minxia,Atherton D P.Optimum Cascade PID Controller Design for SISO Systems[J].IEEE,Control, 1994(1):606-611.

[4] Aidan O'Dwyer.PI and PID Controller Tuning Rules: an Overview and Personal Perspective[J].ISSC,Signals and Systems,2006,161-166.

[5] 阮 毅,陈维均.运动控制系统[M].北京:清华大学出版社,2006.

[6] 王 雪.基于SISO Design Tool设计系统的 PID整定[J].自动化技术与应用,2006,25(9):9-11.