基于小波神经网络的水库来水量预测模型

张 伟 王聪聪 马文丽 徐 英

(1.河海大学水利水电工程学院,南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;3.河海大学水资源高效利用与工程安全国家工程研究中心,南京 210098;4.河海大学水文水资源学院,南京 210098)

水资源是一种特殊资源,既是人类社会赖以生存和发展的必要条件,又是人类活动必不可少的重要资源.目前,全国农业每年缺水约300亿m3,农村2 000多万人口饮水困难,在全国660多个建制市中,有400多个城市供水不足,100多个城市严重缺水,每年因缺水而造成工业损失约200亿元.因此水资源规划管理、开发利用与节约保护,尤其是水资源的优化配置与保护是新时期水利工作的重点之一.水库来水量预测作为水资源优化配置的重要组成部分,在水资源可持续开发利用、国民经济建设中有广泛应用,经济效益巨大[1].

目前,水库来水量预测方法主要有统计学方法,神经网络方法,灰色系统方法,周期分析法,水文要素相关,时间序列等方法.由于水库来水量设计的水文地质因素众多,年际间呈现相当大的随机性和不确定性,各因素之间存在这复杂的非线性关系,各种方法均有其适用场合,因而尚需不断完善和改进.回归分析法是来水量预报中应用最早的方法之一,至今仍是实际工作中的一种重要手段,但是往往需要其它资料(如降雨资料),在资料不全的地区的应用有所限制[2];神经网络具有容错性、抗干扰性和自适应强的优点,比传统的统计模型有优越性,但也有容易收敛到局部最小点、训练时间长等缺点[3].本文将小波理论加入到神经网络中,采用小波神经网络方法对来水量进行预测,并加以实例建模,并与BP模型预测比较,看以看出小波神经网络预测模型的精度比BP模型的高.

1 小波理论

小波分析理论是20世纪80年代中期发展起来的一门新技术,被公认为是工具和方法上的重大突破.小波分析针对傅立叶变换的不足发展而来,傅立叶变换是信号处理领域中最广泛的一种分析手段.傅立叶变换有着严重的缺点:变化之后使信号失去了时间信息,不能告诉人们在某段时间里发生了什么变化,即傅立叶变换在时域中没有分辨能力.而小波分析具有多分辨率分析特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态进行动态调整,这在理论和实用中都有重要的意义,已成功应用于逼近论,分形识别,非线性科学等方面[4-5].

小波是一种长度有限、平均值为0的波形.所谓小波(wavelet)就是“很小的波”,一类具有震荡性、能够快速衰减到零的函数.其数学上的定义为

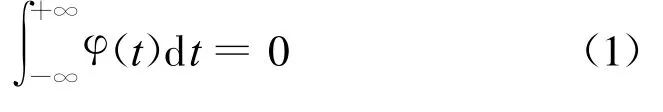
称满足(1)式的小波为基本小波.它的特点包括[6]:①基本小波能量小,形体小,即在时域上的持续时间是有限的,最好有紧支撑性质;②小波在时域上有震荡性,同时具有良好的消失矩性质;③直流分量为0.

小波变换是指把某一基本小波函数φ(t)平移τ后,在不同尺度a下与待分析的信号x(t)做内积.

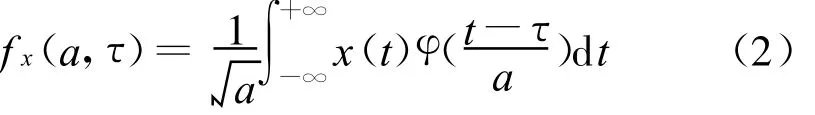
等效的时域表达式为

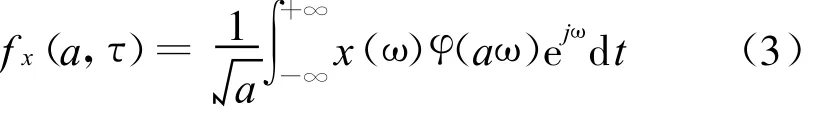
式中,τ和a是里面的参数,τ相当于使镜头相对于目标平行移动,a相当于使镜头向目标推进或远离[7].

根据小波函数的定义,小波函数具有多样性,不同的情况需要不同的小波函数.目前广泛使用的小波函数有 Harr小波、Daubechies小波、Morlet小波、Mexican hat小波、Gauss小波、正交小波和样条小波等.目前往往是通过不断的实验(对结果进行对比分析)来选择小波函数.本文中小波基函数采用国外较多使用的Morlet母小波基函数,数学公式为

2 小波神经网络

小波神经网络是结合小波变换理论与人工神经网络的思想而构造的一种新的神经网络模型,是由法国著名的信息科学研究机构IRISA的Zhang Qinghua等提出[8].小波神经网络避免了BP神经网络结构设计的盲目性和局部最优等非线性优化问题,结合了小波变换良好的时频局域化性质以及神经网络的自学习能力,简化了训练,具有较强的函数学习能力和推广能力[9-10].

小波神经网络与BP神经网络的主要区别就是用非线性小波基函数取代了BP神经网络通常用的非线性Sigmoid函数,作为隐含层节点的传递函数.在输入信号序列为xi(i=1,2,…,k)时,隐含层输出计算公式为[5]

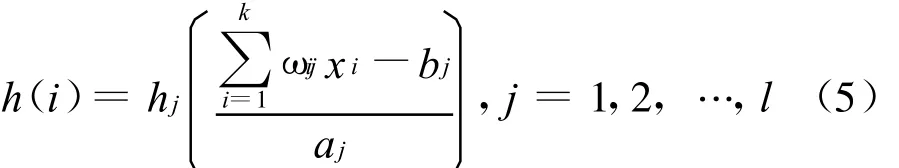
式中,h(i)为隐含层第i个节点输出值;ωij为输入层和隐含层的连接权值;bj为小波基函数hj的平移因子;aj为小波基函数hj的伸缩因子;hj为小波基函数.输出层计算公式:

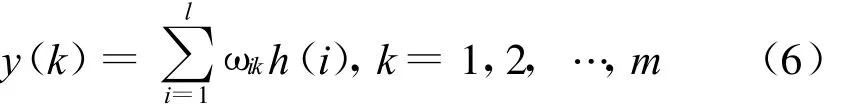
小波神经网络具体训练步骤[11]:

Step1:网络的初始化,网络连接权重ωk,平移因子bk,小波函数伸缩因子ak取随机初始值,设置网络学习速率.

Step2:为网络提供一组学习样本,用于训练网格,再提供一组测试样本,用于测试网格预测精度.

Step3:利用当前网络参数计算网络的实际输出.

Step4:把训练样本输入网格,计算网络预测输出,并计算网格的输出误差E.

Step5:当E小于容许的误差ε或达到指定的迭代次数时,学习过程结束,否则进行误差反向传播,转向Step6.

Step6:利用梯度下降法求网络参数的变化及误差反向传播.

3 实例建模

某水库位于深圳宝安县西南部,1957年4月竣工.集水面积64km2,最大库容6840万m3.现有此水库1957～2006年的来水量资料,利用小波神经网络算法,对水库1957～2006年的水库来水量进行预测分析.1957～1996年数据用于网络训练,1997～2006年的数据用于网络验证.为了说明小波网络预测的好坏,同时还进行了BP神经网络预测.小波网络的隐层单元数由网络自行确定,而BP神经网络需要靠经验确定.

根据水库来水量的特性,设计小波神经网络,分为输入层、隐含层和输出层3层.其中,输入层为当前年的前n年的来水量,隐含层节点由小波函数构成,输出层为当前的预测来水量[12].经过反复试算,确定输入层为5个节点,即由前5年的来水量预测第6年的来水量.确定只有一个隐含层,隐含层的神经元个数为20,小波神经网络的建模自适应强,不必人为确定隐含层神经元个数,可以自动寻优[13],最终寻优结果为10.运用 Matlab编写程序,最大迭代次数为400,得到的训练样本的预测曲线如图1所示.同样取输入层为5个节点,隐含层神经元为20,对来水量数据进行预测,得到训练样本预测曲线如图2所示.

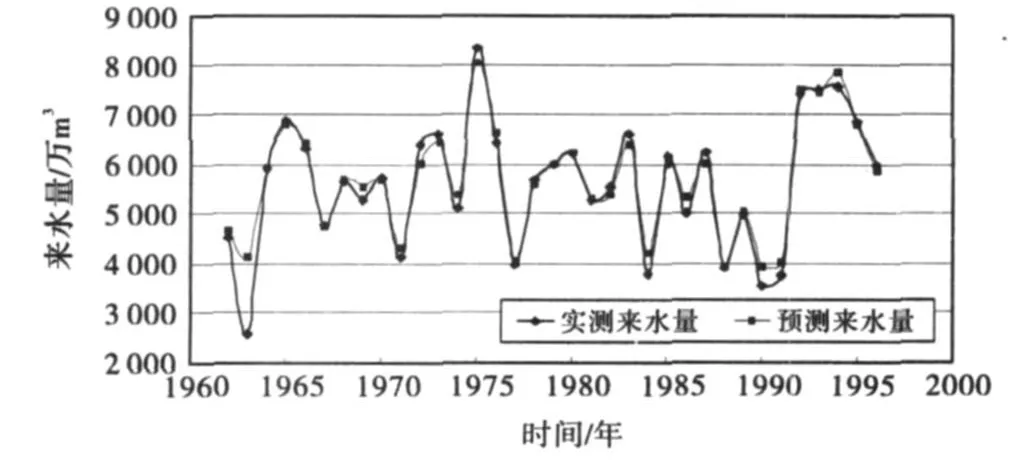
图1 小波神经网络训练样本拟合曲线

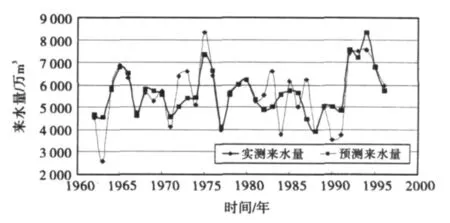
图2 BP神经网络训练样本拟合曲线

图1中曲线的复相关系数R=0.945,图2中曲线的复相关系数为R=0.846,可见小波神经网络模型的拟合精度明显高于BP模型.再用此训练好的网络对1997～2006年的来水量进行预测,预测结果见表1和图3.

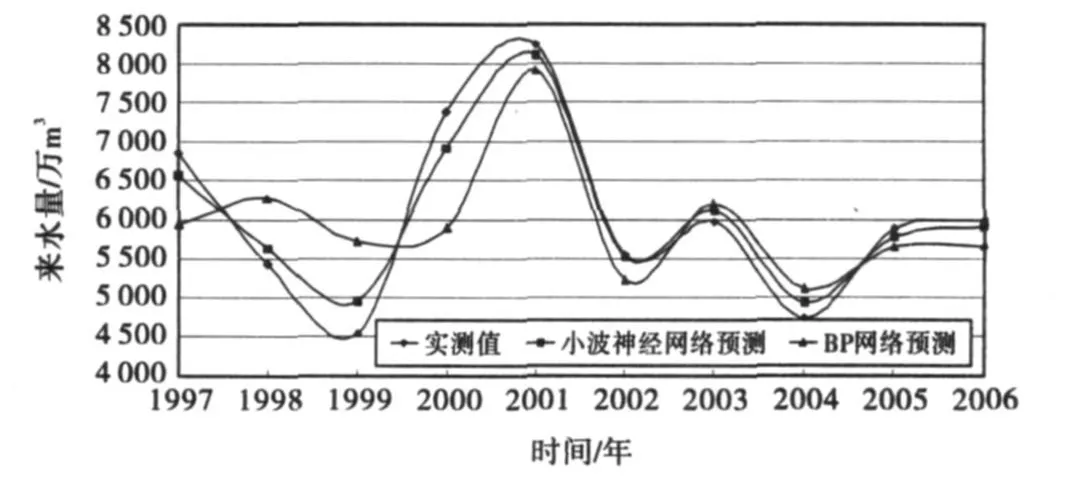
图3 两种方法的来水量预测对比

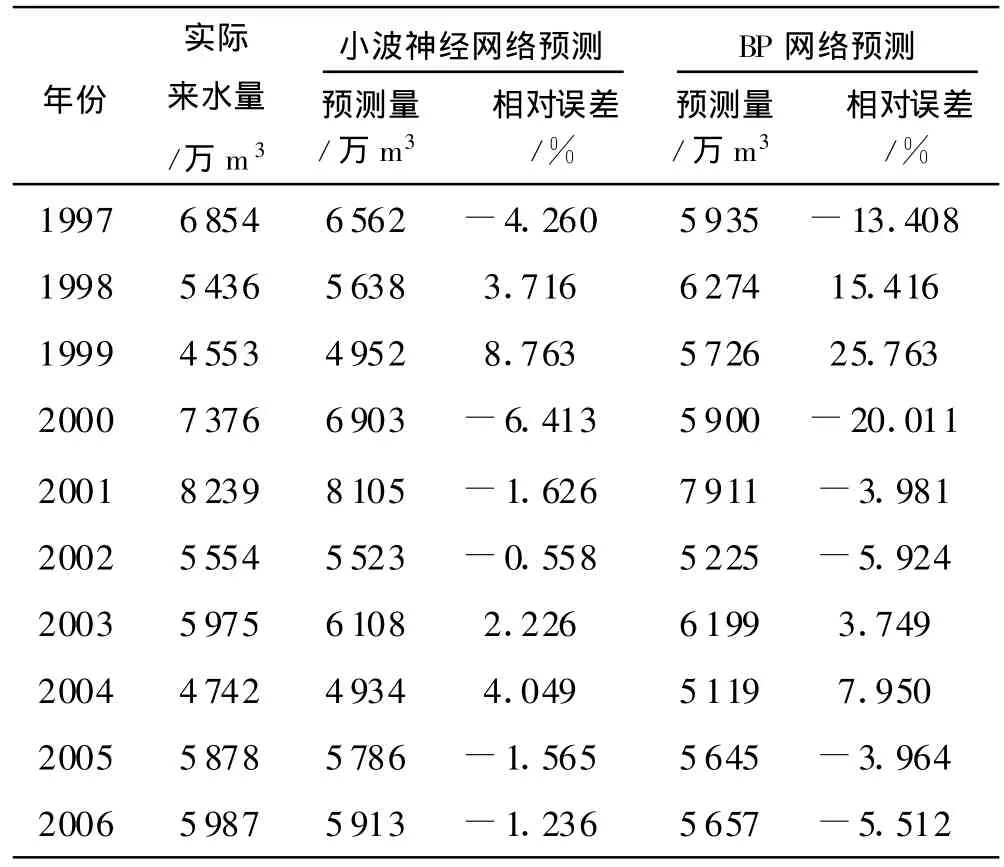
表1 实测来水量与预测值

由以上实测来水量与预测值的精度表可以看出,小波神经网络预测来水量的精度明显高于BP网络,最大相对误差不超过10%,平均相对误差为3%左右,精度达到了预测的要求.

4 结 论

本文采用小波神经网络对水库的来水量进行预测,本质是将神经网络与小波分析相结合.研究表明其本身适合对波动性的信号进行预测,并且在神经网络节点数相同的情况下,小波神经网络比BP神经网络具有更高的预测精度.此模型取得了比较好的预测效果,可以用于水库来水量的预测.

[1] 闻建伟,张德民.水库逐月来水量预测方法研究[J].黑龙江水利科技,2009(1):154-154.

[2] 晏 玲,张世强,张小文.气象水文耦合的三峡水库入库水量预报研究[J].人民长江,2009,24:26-33.

[3] 邢茂琳,周新志.都江堰涞水预测中BP网络训练方法的研究[J].微计算机信息,2009,25(12-1):149-150.

[4] 岳荣花.小波神经网络在沉降预测中的应用研究[D].南京:河海大学,2007.

[5] 张红英,吴 斌.小波神经网络的研究及展望[J].西南工学院学报,2002,17(1):8-10.

[6] 汤成友,官学文,张世明.中长期水文预报[M].北京:中国水利水电出版社,2008.

[7] 史 峰,王小川.MA TLAB神经网络 30个案例分析[M].北京:北京航空航天大学出版社,2010.

[8] Zhang Qinghua.Bmvenlste A.Wavelet Networks[J]. IEEE Trans.On Neutral Networks,1992,3(6):889-898.

[9] 洪锦祥,黄 卫.小波神经网络预测混凝土强度研究[J].工业建筑,2004,34(7):47-49.

[10]许后磊,储冬冬.基于改进阀值的提升小波变换在探地雷达信号去噪中的应用[J].三峡大学学报:自然科学版,2010,32(2):42-47.

[11]曹红林,王靖涛.用小波神经网络预测深基坑周围地表的沉降量[J].土工基础,2003,17(4):58-60.

[12]马吉刚,崔远来.水库来水量预测的进化神经网络法[J].中国农村水利水电,2005(2):35-37.

[13]刘洪波.城市供水管网水量预测的小波神经网络方法[J].天津大学学报,2005,38(7):636-639.