基于多核PC软件雷达信号处理实时性仿真

徐文利，察豪，周沫，张光宇

（海军工程大学电子工程学院，湖北武汉 430033）

0 引言

由于不同用途的雷达其信号参数完全不一样，所以造成目前设计研制的雷达往往功能单一、体制单一、无法适应在不同的环境下对不同属性的目标进行智能化跟踪探测的需要。如果能把软件雷达的概念应用于雷达的设计研制，那么就能比较圆满地解决目前雷达设计所存在的上述问题。软件雷达的概念借鉴于软件无线电，其主要思想是在尽可能少更换或不更换硬件的前提下，利用软件在同一个雷达硬件平台上重新定义其功能并实现多功能，具有很强的灵活性［1－3］。这个灵活性的实现依赖于ADC的位置，离天线越近，灵活性越好。在ADC之后，就进入了数字信号处理部分。由于雷达是一个实时性很强的系统，因此，对ADC后的数字信号实时性研究，是雷达信号处理能否进行软件化的前提。本文通过常用警戒雷达的信号处理流程，针对信号处理每个模块的运算量和运算时间进行了详细的研究，对雷达视频信号进行软件化且满足实时性，提供了很好的参考价值。

1 雷达信号处理仿真模型

一般雷达是通过发射电磁波，再从回波中检测目标的。在回波当中，不但有目标回波，也会混杂着噪声、杂波和干扰。所以雷达探测目标是在十分复杂的信号背景下进行的，雷达需要通过信号处理来检测目标，并提取目标的各种有用信息。雷达的信号处理功能有很多，不同的雷达采用的功能也有所不同。本文以常用的警戒雷达信号处理流程进行分析，其仿真模型见图1［4－5］:

图1 警戒雷达信号处理仿真模型Fig.1The simulation model of guard radar's signal processing

2 信号处理系统中各功能模块运算复杂度分析

2.1 脉压模块

1）运算模型

脉压是大时宽带宽积信号通过1个脉冲压缩滤波器实现的，可以解决距离和距离分辨力之间的矛盾。实现脉冲压缩可以在时域进行，也可以在频域进行。实际工程实现时，往往是在频域实现的，因为对于采样点数较多时，可以利用FFT算法提高计算速度，其流程为首先计算出雷达回波和匹配滤波器的FFT，然后将雷达回波与匹配滤波器的FFT结果在频域相乘，再对相乘结果经IFFT变换，从而得脉压处理的结果，比卷积大大降低了运算量，其运算模型如图2所示［6－7］:

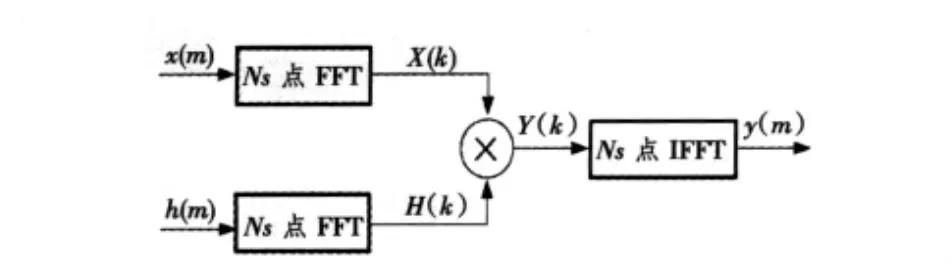
图2 脉冲压缩处理的频域实现模型Fig.2The realization model of pulse compressing processing in frequency domain

2）运算量

设I和Q两路A/D采样点都为Ns点，两路合成Ns个复数点。由图1可知，脉压使用2个复数FFT，1个复数IFFT和Ns个复数乘法生成Ns个脉压输出。其中，匹配滤波器的FFT可以事先算好，放入缓存当中，计算脉压时，可直接拿来使用。习惯上，Ns常取2的n次方，以利于FFT的计算。

2.2 MTI对消模块

1）运算模型

MTI的用途是抑制来自建筑物、山、树、海和雨之类固定的或慢动的无用目标信号，提高雷达信号的信杂比，以利于运动目标检测。MTI利用动目标回波的多普勒频移来区分动目标和固定目标。它利用固定地物的多普勒频率为0的特点，采用跨周期相消方式抑制掉回波中的固定地物杂波。实际工程应用得比较多的是多次对消器，其输出为:

其中，K为对消的次数;ωi为对消器的系数。K次对消器的仿真模型如图3所示。

图3 K次对消实现模型Fig.3The realization model of K times cancel

图3中xn（m）表示第n个发射周期，第m个距离门的回波信号。

2）运算量

设I和Q两路A/D采样点都为Ns点，两路合成Ns个复数点，由图3可知，每个复数点需要K+1次复数乘法和K次复数加法。因此，K次对消器所需要的运算量为:Ns×（K+1）次复数乘法，Ns×K次复数加法。

2.3 动目标检测（MTD）模块

1）运算模型

动目标检测（MTD）是由于MTI对地物杂波抑制能力有限，根据最佳匹配滤波，在MTI之后级联匹配滤波器构成，实现输出信噪比最大，提高目标的检测性能。匹配滤波器组的实现方式有2种:一种是在时域采用FIR实现，另外一种是FFT在频域实现。

2）运算量

设I和Q两路A/D采样点都为Ns点，两路合成Ns个复数点，回波采用16个通道进行滤波，当采用FIR方式时，每个复数点需要16次复数乘法和15次复数加法，因此，Ns个复数点所需要的运算量为: Ns×16次复数乘法，Ns×15次复数加法。当采用FFT方式时，需要进行Ns个16点复数FFT。

2.4 求模模块

1）运算模型

求模模块的功能是对I和Q两通道进行检波，用于后面的CFAR处理。其运算模型是:

m为第m个距离单元。

2）运算量

设I和Q两路A/D采样点都为Ns点，两路合成Ns个复数点，因此，求模的运算量为Ns×2次实数乘法，Ns次实数加法，Ns次实数开方。

2.5 恒虚警处理（CFAR）模块

1）运算模型

恒虚警处理（CFAR）是保持信号检测时的虚警概率恒定，使处理器不致于因虚警太多而过载。其实现方法是采用自适应门限代替固定门限，此自适应门限能随着被检测点的背景噪声、杂波和干扰的大小自适应的调整。恒虚警处理分为慢门限CFAR和快门限CFAR。慢门限CFAR主要针对接收机内部噪声，快门限CFAR则主要针对杂波环境下的雷达自动检测。本文主要讨论平均单元选大快门限CFAR，其仿真模型如图4所示［8－9］。

图4 CFAR单元平均取大实现模型Fig.4The realization model of GO-CFAR

2）运算量

设I和Q两路A/D采样点都为Ns点，两路经检波合成Ns点实数，以被检测单元左右2个保护单元，左右16个单元平均取大为例:假如第0个距离单元到第18个距离单元和第Ns－18个距离单元到Ns个距离单元不参与平均单元计算，那么每个单元需要进行30次实数加法和2次除法。因此，总共所需要的运算量为:（Ns－36）×30次实数加法、（Ns－36）×2次除法和（Ns－36）次比较。除法在编程实现时，可以采用向右移四位算出，比采用除法函数要快得多。

3 信号处理系统中各功能模块仿真时间

根据对各个信号处理模块的运算量分析，分别采用常规方法和IPP（集成性能原件）［10］算法库的方法对各处理模块的实现进行耗时仿真，计算步骤和结果如下:

3.1 脉压模块

1）常规、IPP脉压计算步骤和区别

脉冲压缩在频域实现，其主要的计算归结于FFT和IFFT的实现。

Ns点FFT和IFFT常规实现步骤:首先计算出Ns点旋转因子的值，存储成表，放在内存中，供后面Ns点FFT和IFFT计算时用;接着将x（m）码位倒置，使得输出的Ns点FFT和IFFT结果是顺序的;最后进行蝶形单元计算，得出Ns点FFT和IFFT的计算结果。

Ns点FFT和IFFT的IPP实现步骤:首先，利用函数ippsFFTInitAlloc_C_32fc（IppsFFTSpec_C_32fc＊＊ppFFTSpec，int order，int flag，IppHintAlgorithm hint）［10］进行内存分配和初始化FFT和IFFT计算复数信号的上下文环境。初始化主要包括计算的点数，FFT和IFFT结果是否归一化，FFT和IFFT计算以计算精度还是计算速度为主;接着利用函数ippsFFTFwd_CToC _32fc_I（Ipp32fc*pSrcDst，const IppsFFTSpec_C_32fc *pFFTSpec，Ipp8u*pBuffer）［10］和ippsFFTInv_ CToC_32fc_I（Ipp32fc*pSrcDst，const IppsFFTSpec_C _32fc*pFFTSpec，Ipp8u*pBuffer）［10］进行FFT和IFFT复数计算，最后利用函数ippsFFTFree_C_32fc （IppsFFTSpec_C_32fc*pFFTSpec）［10］关闭FFT和IFFT计算复数信号的上下文环境，释放分配的内存。

2）仿真结果

根据上述计算步骤，分别对FFT、IFFT采用常规方法和IPP计算方法，在四核2.34G CPU的工控机上进行了10 000次蒙特卡罗仿真，得出仿真时间结果见图5和图6。

3.2 MTI K次对消模块

1）常规、IPP MTI K次对消计算步骤和区别

首先计算出每个对消系数和每个回波Ns点采样进行相乘，然后把这K+1个脉冲的每个回波单元进行相加，最后把进行过相加的Ns个回波单元存放在

2）仿真结果

根据上述计算步骤，以MTI 6次对消为例，分别采用常规方法和IPP计算方法，在四核2.34G CPU的工控机上进行了10 000次蒙特卡罗仿真，得出仿真时间结果见图7和图8。预先设置的缓存里，供下一步处理用。2种方法的区别是在进行for（）{}循环时，一个调用的是常规复数乘、加法函数，另一个用的是IPP复数乘、加法函数: ippsMul_32fc（const Ipp32fc*pSrc1，const Ipp32fc* pSrc2，Ipp32fc*pDst，int len）［10］，ippsAdd_32fc（const Ipp32fc*pSrc1，const Ipp32fc*pSrc2，Ipp32fc* pDst，int len）［10］。

3.3 动目标检测（MTD）模块

1）常规、IPP动目标检测计算步骤和区别

本文中MTD主要进行了窄带多普勒滤波器组滤波的研究，采用FFT进行实现。常规和IPP实现步骤同脉压FFT。

2）仿真结果

根据上述计算步骤，以16点FFT进行Ns次循环为例，分别采用常规方法和IPP计算方法，在四核2.34G CPU的工控机上进行了10 000次蒙特卡罗仿真，得出仿真时间结果见图9和图10。

3.4 求模模块

1）常规、IPP求模计算步骤和区别

根据I、Q两路信号进行Ns点求模。2种方法的区别是:一个是求出1点的幅度，然后进行Ns点for （）{}循环，另一个用的是IPP复数求模函数: ippsMagnitude_32fc（const Ipp32fc*pSrc，Ipp32f* pDst，int len）［10］。

2）仿真结果

根据上述计算步骤，分别对求模采用常规方法和IPP计算方法，在四核2.34G CPU的工控机上进行了10 000次蒙特卡罗仿真，得出仿真时间结果见图11和图12。

3.5 快门限单元取大CFAR模块

1）常规、IPP快门限单元取大CFAR计算步骤和区别

图11 IPP求模仿真时间Fig.11The simulation time of magnitude in using IPP way

图12 常规求模仿真时间Fig.12The simulation time of magnitude in using conventional way

根据求模后的结果，对从第18个单元到Ns-18个单元的每个点进行左右16个点的求和，然后得出其平均值，进行比较，把得出的结果存储到相应距离单元，作为自适应门限值和本单元的回波强度值进行比较。2种方法的区别是:在进行for（）{}循环时，一个用的是常规求和和除法计算，另一个用的是IPP求和和除法函数:ippsSum_32f（const Ipp32f*pSrc，int len，Ipp32f*pSum，IppHintAlgorithm hint）［10］和ippsDiv_32f_I（const Ipp32f*pSrc，Ipp32f*pSrcDst，int len）［10］。

2）仿真结果

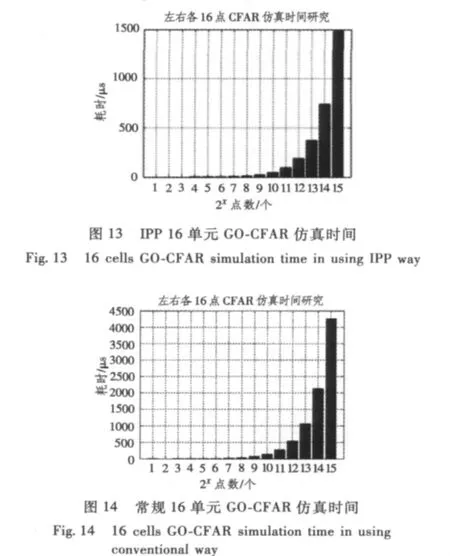
根据上述计算步骤，以被检测单元左右2个保护单元，左右16个单元平均取大为例，分别采用常规方法和IPP计算方法，在四核2.34G CPU的工控机上进行了10 000次蒙特卡罗仿真，得出仿真时间结果见图13和图14。

4 结语

雷达视频信号处理软件化过程中，不管雷达型号、采样频率、雷达重复周期、量程如何，本质都是采样点数的问题，实时性就是这些采样点在规定的时间内完成相应的计算。根据图5～图14可知，采用IPP算法比采用常规算法计算速度要高1～2个数量级，在1 500 μs内，回波采样点数在32 768个以内，脉压、MTI、求模和CFAR都可以满足实时性要求，16通道动目标检测（MTD）在2 000 μs内，回波采样点数在8 192个以内，可以满足实时性要求。

［1］Muursepp．Software Radar［Z］．IEEE，2008，4（84）．

［2］ZHANG Hui，LI Lin，WU Ke．Software-defined six-port radar technique for precision range measurements［J］．IEEE Sensors Journal，2008，8（10）:1252－1255．

［3］BARTENE V G．Software radar new reality［Z］．IEEE，2006:445－448．

［4］GRYDELAND T，LING F D，ERICKSON P J，HOLT J M．Software radar signal processing［J］．Annales Geophysical，2005，23:109－121．

［5］YANG Wan-hai．Model and simulation of radar system［M］．Xi'an:Xi'an Electronical Science and Technology University Press，2007．187－188．

［6］SCHULTE M．A low-power multithreaded processor for software definedradio［Z］．JournalofVLSISignal Processing，2006:143－159．

［7］SHI Yan-bin，TAN Zhong-ji，WANG Yan．Research of radar signal processor based on the software defined radio［Z］．IEEE，2007:1252－1255．

［8］DU Peng-fei，ZHANG Xiang-jun．A new conclusion in CACFAR detection［J］．Modern Radar，2007，29（2）:60－62．

［9］ANTONIO G，MARIO M，PEDRO S．Electronic protection and routing optimization of MANETs operation in an electronic warfare environment［J］．2007，5（8）:1031－1045．

［10］Intel Integrated Performance Primitives Reference Manual［M］．Intel Corporation，2008．