基于多属性群决策的舰船维修方案组合评估方法

訾书宇，魏汝祥，王丹

（1．海军工程大学装备经济管理系，湖北武汉430033;2．海军工程大学理学院，湖北武汉430033; 3．中国船舶重工集团公司第七一四研究所，北京 100192）

0 引言

舰船装备维修是一项复杂的系统工程，维修方案的优劣将会对舰船的可靠性和作战能力产生直接影响。如何评价维修方案的优劣，传统的做法是装备维修管理部门依据以前的历史经验对不同维修方案可能产生的效果进行预测，并以预测结果作为优选方案的判断标准。从实践运行效果来看，由于传统方法受人为主观因素影响较大，维修方案评估将很难保证科学性和合理性，尤其是在舰船装备结构系统日益复杂的今天。因此，如何从多个维修方案中择优选取，就成为目前舰船维修决策需要重点研究的一个问题。虽然当前学术界已发展了多种方案评估方法，例如层次分析法［1］、灰关联度法［2］、数据包络分析法［3］、熵值法［4］以及模糊综合评判法［5］等，这些方法在一定程度上消除了方案评估中人为主观因素的影响，且保证了方案评估一定的客观公正性，但由于每一评估方法在评估时考虑的信息侧重点有所不同，对于同一方案，采用不同的评估方法可能就会得到不同的结果。由于每一评估方法均利用了方案的某种信息，所以每一评估方法的结果又具有一定的合理性。鉴于此，本文提出采用一种组合评估方法对舰船维修方案进行评估，即首先利用多种单一评估方法分别得到舰船维修方案的评估结果，然后再将这些评估结果进行组合，以组合后的评估结果作为舰船维修方案优选的依据，这样可最大限度地保证评估结果的准确性和权威性。该方法的关键在于设计一个科学合理的评估结果组合方式，本文拟借鉴多属性群决策方法［6］，构建舰船维修方案的组合评估模型，即将每一评估方法得到的评估结果看成是多属性群决策中一名领域专家的决策意见，然后采用一种专家权重动态赋权法，将众专家的决策意见集中成一个每名专家均可以接受的决策意见，该决策意见即为组合评估模型的最终输出结果。

1 舰船维修方案组合评估模型

假设某型舰船维修，备选的维修方案集X= {x1，x2，…，xn}，根据既定的评估指标，分别使用m个单一评估方法对每一维修方案的维修效果进行评估，能得到n个方案的m组不同排序结果:

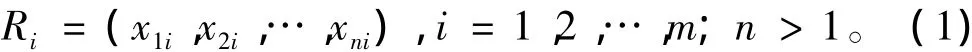
式中:xni表示用第i个评估方法计算得出的第n个方案的维修效果的排序名次。

假设存在1个组合排序结果Y，其与m组评估结果均应具有较高的相关性。不妨用斯皮尔曼等级相关系数［7］表述组合排序结果Y与m组评估结果的相关性，建立组合评估模型如下

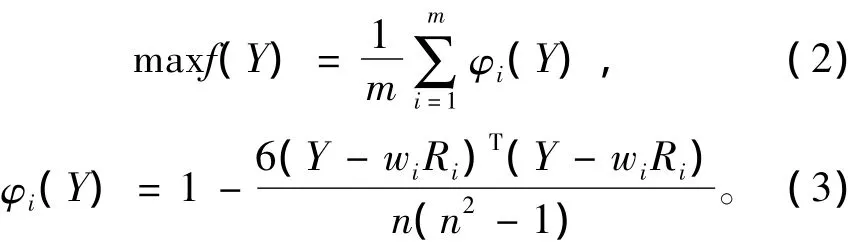
其中:Y=（y1，y2，…，yn）;f（Y）为Y与m组评估结果的平均斯皮尔曼等级相关系数;φi（Y）为Y与第i组评估结果的斯皮尔曼等级相关系数;wi为第i个评估方法的权重

2 基于多属性群决策的权重系数wi求解

由式（5）可知，求解出1组最优的权重系数wi，就可得到最优的Y。本文拟采用多属性群决策方法，对权重系数wi进行求解。首先将上述问题中的m个评估方法看成是多属性群决策中的m名领域专家，则m组排序结果即为m名领域专家的个人决策结果。然后上述问题中对评估方法权重系数wi的求解就可转化为多属性群决策中对专家权重系数的求解。目前，专家权重系数的求解方法很多，一般可分为2类:一是主观赋权法，如特征向量法、最小平方和法［8］等;二是客观赋权法，如离差分析法［9］、主成分分析法等。主观赋权法往往简单可行、操作方便，但易受决策者知识、能力、经验等限制，随意性很大，不同的决策者给出的结果千差万别，直接影响到决策的科学性与合理性［10］;客观赋权法虽然具有对已知信息客观处理的优点，但得出的结果有时会与实际情况相悖，而且解释性较差。因此，主、客观赋权法均具有一定的局限性。为此，本文提出采用一种专家权重动态赋权法，来求解专家权重。该方法的思想是:首先在第一轮决策中，赋予m名领域专家相同的权重（因为我们无法否认每一评估方法的合理性），用简单线性加权法对每名专家的个人决策结果进行组合形成群决策结果，然后比较个人决策结果与群决策结果的一致性，如一致性较差，说明专家之间还没有形成很好的共识;其次在第二轮决策中，按个人决策结果与群决策结果的一致性大小，分别对专家权重进行调整，根据调整后的权重，同样采用线性加权得到第二轮的群决策结果，该结果与上一轮的群决策结果进行比较，如果偏差小于某一阈值，说明群决策结果比较稳定，专家之间共识度较高，该群决策结果为最终的组合评估结果，如偏差大于该阈值，说明群决策结果不稳定，专家仍没有达成广泛共识，仍需对专家权重进行调整，重复第二轮决策过程，直到群决策结果趋于稳定，专家之间达到一个满意的共识度水平。

2.1 问题描述

2.2 专家权重动态赋权

群决策是一个专家协商的过程，其应遵循“少数服从多数”的原则，即当1名专家与大多数专家的决策结果一致时，该专家就应该拥有较大的决策权力，相应的专家权重就应该较大;与此相反，当该专家与大多数专家的决策结果一致性较差时，其决策权力就应该较小，相应的专家权重就应该较小。为叙述方便，我们记第i位专家与专家群体的一致性程度为λi。下面我们构造对专家决策权力的动态赋权模型，模型求解步骤如下:

步骤1:赋予m名专家初始权重，由于我们无法确切知道每一专家的能力大小，即无法否认每一评估方法的合理性，所以设每一专家的初始权重均为1/m，由式（6）得初始的群决策结果为Y=（y1，y2，

步骤2:计算专家di的个体决策结果Ri与群决策结果Y的一致性程度λi，设λi为n×1矩阵，λi= （λ1i，λ2i，…，λni）T，定义

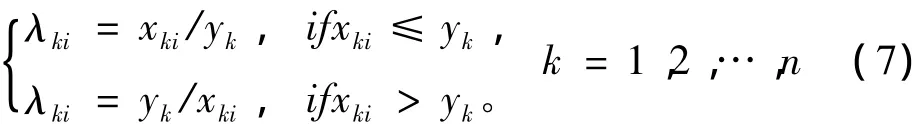
据此定义，可知个体决策结果Ri与理想的群决策结果Y的一致性程度λ*=（1，1，…，1）T，个体决策结果Ri与负理想的群决策结果Y的一致性程度λ＊＊=（0，0，…，0）T;

步骤3:计算个体决策结果Ri与理想群决策结果和负理想群决策结果的接近程度，我们用欧式距离度量接近程度，即

步骤4:计算个体决策结果Ri与群决策结果的综合接近程度，引入参数αi，设其是Ri与理想群决策结果的相似度，则1－αi就是Ri与负理想群决策结果的相似度，综合接近程度的度量公式为:

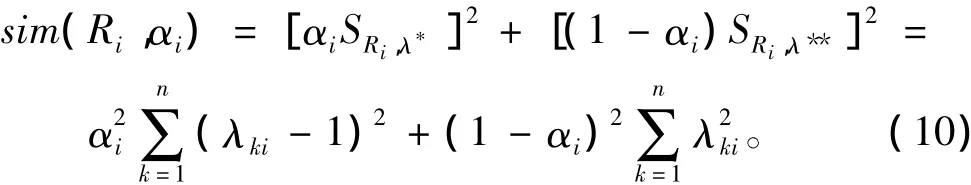
令dsim（Ri，αi）/dαi=0，可得Ri与理想群决策结果的相似度

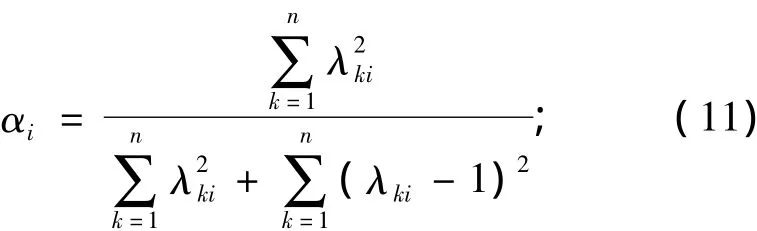
步骤5:对专家权重进行调整。依据Ri与理想群决策结果的相似度大小，对每一专家的权重进行重新调整，调整的公式为

3 实例分析

下面通过一个例子来说明这种方法在舰船维修方案决策中的应用。

假设某型舰船维修，有10个备选的维修方案，分别选用层次分析法、模糊综合评价法、BP神经网络法、综合指数法和DEA方法，对10个备选维修方案进行评价，评估结果如表1所示。

如前所述，以上5种评估方法的计算结果可看成5个专家的个体决策结果，首先给出专家初始权重w=（0.2，0.2，0.2，0.2，0.2），由式（6）求得的初始群体决策结果为Y=（3.4，1.6，1.6，4.6，4.8，7.6，7.4，5.4，8.8，9.8）。设置稳定性阈值参数θ= 0.0001，根据2.2节所描述的赋权过程，经计算得经过9次动态赋权之后，两相邻的群决策结果之间的距离将小于θ，可认为群决策结果已趋于稳定，此时专家权重为:

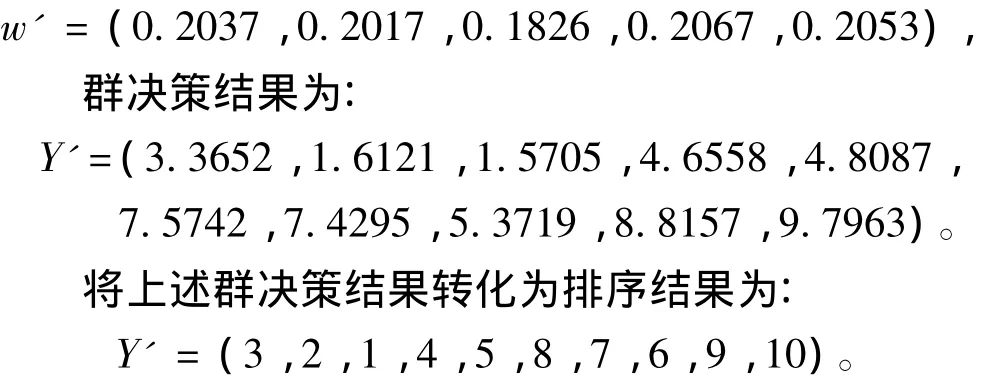
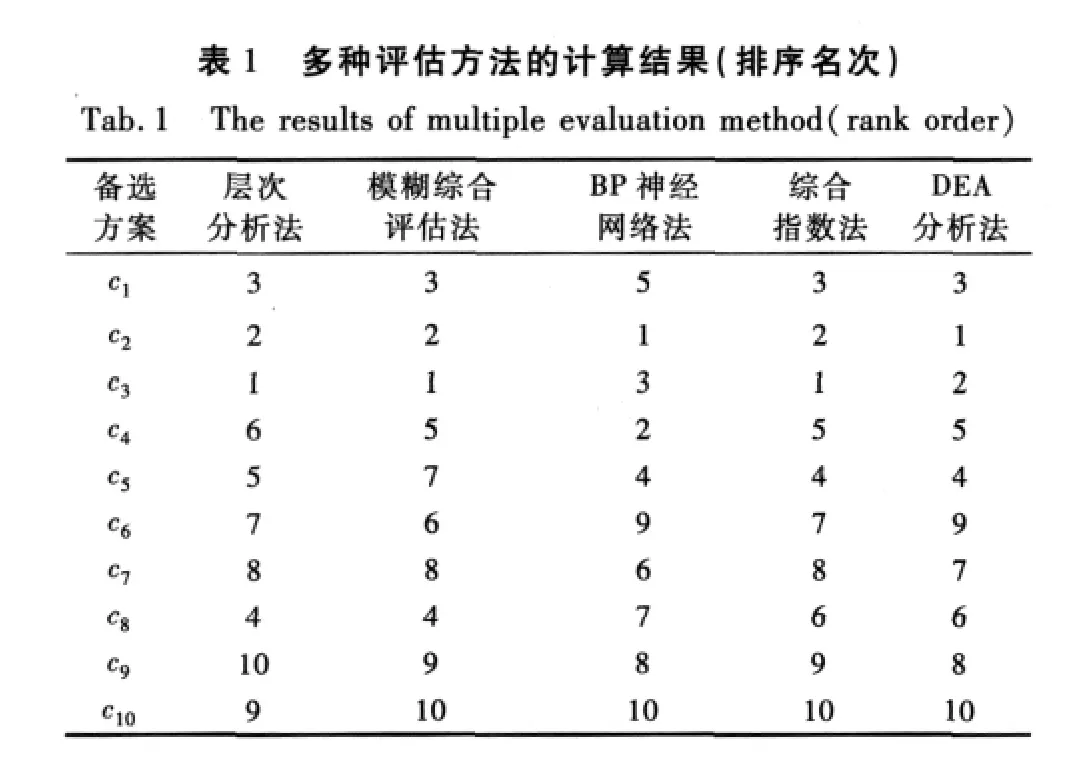
从表1可以看出，该型舰船维修方案的组合评估结果为c3≻c2≻c1≻c4≻c5≻c8≻c7≻c6≻c9≻c10，方案c3为最优方案。用斯皮尔曼等级相关系数计算组合评估结果的可信度，计算结果如表2所示。

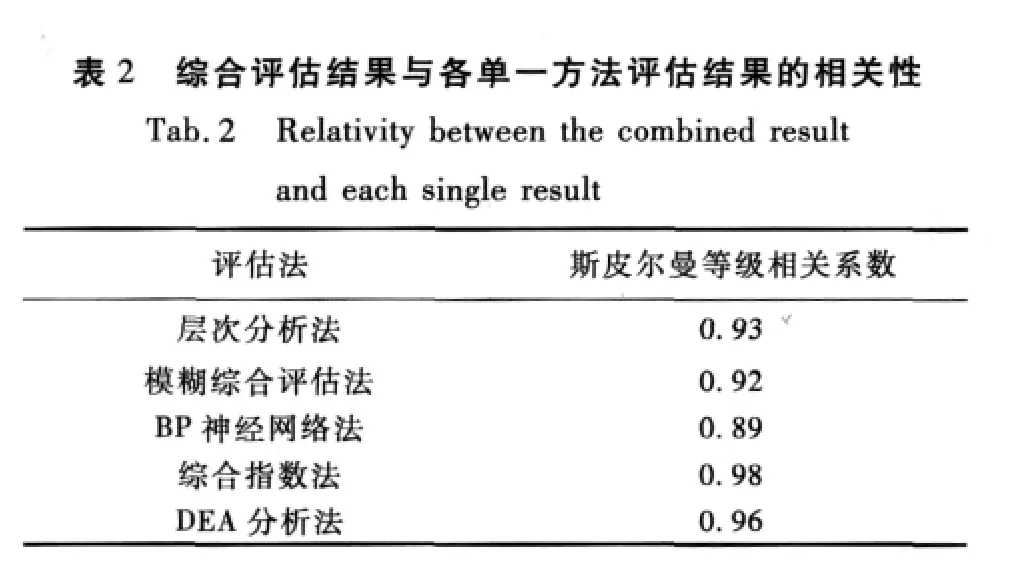
从表2中可以看出，组合评估结果的可信度为: （0.93+0.92+0.89+0.98+0.96）/5=0.936。所以，用本文所提的方法对舰船维修方案进行评估，得出的最优方案为c3，且可信度水平为93.6%;如采用上述5种单一评估方法对维修方案进行评估，得出的最优方案可能为c3或c2，c3的可信度为60%，c2的可信度为40%。由此可知，使用本文所提的组合评估方法对舰船维修方案进行评估，不仅可以得到较为科学合理的评估结果，而且可以保证评估结果具有较高的可信度。

4 结语

算例的结果说明该组合评估方法是可行的。该方法最大程度地利用了每一评估方法的信息量，并通过模拟专家决策思维的多属性群决策方法对评估方法进行组合，提高了评估结果的准确性、科学性，是评估舰船维修方案的一种可靠而有效的方法。舰船维修管理部门可以参照评估的结果，对舰船维修方案进行合理优化，以利于舰船作战能力的充分发挥。另外该模型适用性较强，可以推广应用于其他领域的排序性方案评估问题。

［1］吴力平，冯杨，李刚．基于层次分析法的施工现场平面布置方案评估［J］．浙江工业大学学报，2010，38（1）:111－114．

WU Li-ping，FENG Yang，LI Gang．The evaluation of layout scheme in the construction sites based on the Analytic Hierarchy Process（AHP）［J］．JournalofZhejiang University of Technology，2010，38（1）:111－114．

［2］万树平．布雷方案评估的灰关联度方法［J］．计算机工程与应用，2009，45（32）:206－208．

WANShu-ping．Methodofgreyrelationdegreefor evaluation of minelaying plans［J］．Computer Engineering and Applications，2009，45（32）:206－208．

［3］刘艳，顾雪平，张丹．基于数据包络分析模型的电力系统黑启动方案相对有效性评估［J］．中国电机工程学报，2006，26（5）:32－38．

LIU Yan，GU Xue-ping，ZHANG Dan．Data envelopment analysis based relative effectiveness assessment of power system black-start plans［J］．Proceedings of the CSEE，2006，26（5）:32－38．

［4］鲁泳，廖文和．一种基于信息熵的供应商优选方法［J］．机械制造与研究，2007，36（6）:7－9．

LU Yong，LIAOWen-he．Selectingandevaluatinga supplier of parts based on information entropy［J］．Machine Building＆Automation，2007，36（6）:7－9．

［5］鲍平鑫，杨永伟，吴东广，等．模糊综合评判在军事装备装载加固方案评估中的应用研究［J］．军事交通学院学报，2008，10（4）:17－20．

BAO Ping-xin，YANG Yong-wei，WU Dong-guang，et al．Application of synthetical evaluation based on fuzzy theory to military equipment loading and securing method［J］．Journal of Academy of Military Transportation，2008，10 （4）:17－20．

［6］徐玖平，吴巍．多属性决策的理论与方法［M］．北京:清华大学出版社，2006．

XU Ju-ping，WU Wei．Multiple attribute decision making theory and methods［M］．Beijing:Tsinghua University Press，2006．

［7］李汶华，郭均鹏，王涛，等．彩票与国民经济的关联性分析［J］．天津大学学报（社会科学版），2007，9（6）:521－523．

LI Wen-hua，GUO Jun-peng，WANG Tao，et al．Relation analysis between lottery industry and national economy［J］．Journal of Tianjin University（Social Sciences），2007， 9（6）:521－523．

［8］徐泽水．互补判断矩阵的2种排序方法——权的最小平方和法及特征向量法［J］．系统工程理论与实践，2002，22（7）:71－75．

XU Ze-sui．Two methods for priorities of complementary judgementmatrices-weightedleast-squaremethodand eigenvector method［J］．Systems Engineering-Theory＆Practice，2002，22（7）:71－75．

［9］陈华友．多属性决策中基于离差最大化的组合赋权方法［J］．系统工程与电子技术，2004，26（2）:194－197．

CHEN Hua-you．Combination determining weights method for multiple attribute decision making based on maximizing deviations［J］．Systems Engineering and Electronics，2004，26（2）:194－197．

［10］MA Jiun，FAN Zhi-ping HUANG Li-hua．A subjective and objective integrated approach to determine attribute weights［J］．European Journal of Operational Research，1999，112 （lssue2）:397－404．