捷联式惯导系统仿真器设计

王喜龙，程远，吴汪洋

（1．海军驻431厂军代表室，辽宁葫芦岛125004;2．中国舰船研究院，北京 100192）

0 引言

计算机技术的飞速发展使得捷联系统的设计与分析工作（特别是系统的误差分析工作）可以首先在计算机进行，在此基础上再进行系统的硬件（包括陀螺、加速度计与计算机等）及系统软件（包括各种计算机算法及不同迭代周期的选择等）的设计和选择。但由于条件所限，在不能提供系统硬件的情况下为了进行捷联惯导系统的研究，开发惯导仿真器是必不可少的。

1 捷联惯导系统仿真器的实现

本文针对飞行器用捷联惯性导航系统的工作环境进行仿真，其主要目的是仿真出符合实际惯导系统的误差，捷联惯导系统仿真器包括4个模块:飞行轨迹发生器，惯性敏感元件仿真器（陀螺仿真器和加速度计仿真器），导航计算机仿真器和误差处理器。仿真结构如图1所示［1］。

1.1 飞行轨迹发生器［2－4］

飞行轨迹数据生成是为了测试验证导航软硬件系统实时计算性能而必需的输入信号数据。对于捷联惯导仿真系统，需要2类飞行轨迹数据:飞行姿态数据（姿态角、姿态角转动速率）和飞行轨迹数据（位置、速度、加速度）。实际飞行时，这2类数据的变化是有关联的。如果根据飞机模型和飞行力学原理，用数学的方法来产生一个与实际完全相符的飞行轨迹数据文件，将会因为各飞行轨迹量之间的耦合关系，使数学模型的建立非常复杂，甚至无法建立起精确的数学模型。

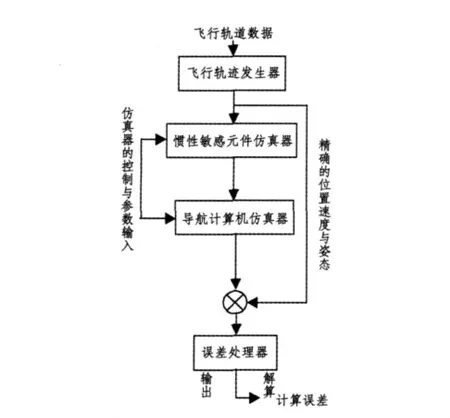
图1 数字仿真器原理方框图Fig．1Principle block diagram of digital simulation

为了简化建模，认为2类数据按照各自独立的规律变化，二者之间的变化没有关系，这样就可以很方便地用数学公式产生出任意时刻精确的理想飞行轨迹数据。测试用飞行轨迹数学模型的基础是相互独立的3个姿态角时间函数、3个位置时间函数。这样计算生成的飞行轨迹虽然不是实际飞行轨迹，但可以很方便地得到任意时刻的精确测试用飞行轨迹数据，用来检验捷联惯导系统仿真器的正确性和精度。

1.1.1 飞行姿态数据生成

设定飞行姿态角是随时间变化的余弦函数（也可以根据需要设定为其他函数）:

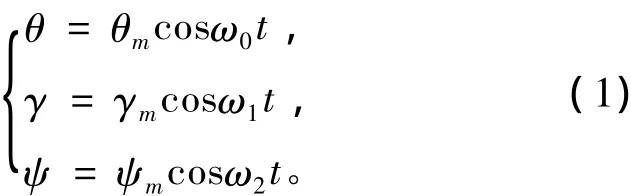
机体系相对于地理系的转动角速率ϖ在机体系中的投影为:

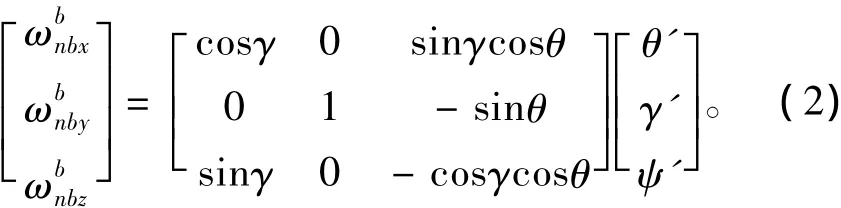
1.1.2 飞行轨迹数据生成

设定位置（纬度、经度、高度）的变化规律为时间的正弦函数（也可以根据需要设定为其他函数），并计算出位置的一阶和二阶导数:

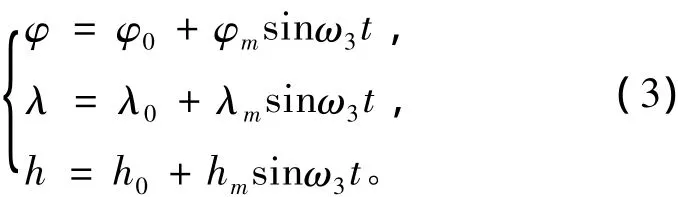
计算出地球直角坐标系中飞行载体位置所对应的直角坐标系R（x，y，z），并求直角坐标的一阶和二阶导数，

其中，R′为导航系相对于地球的速度在地球坐标系中的投影。

在地球系中的相对于地球加速度在导航系中的投影和在导航系中的相对于地球加速度在导航系中的投影为:

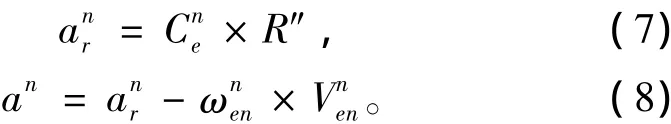
其中，R″为相对于地球加速度在地球系中的投影。

1.2 惯性敏感元件仿真器

惯性敏感元件仿真器给出陀螺与加速度计的仿真模型。当只研究计算机的算法误差时，则不考虑敏感元件的误差;当研究敏感元件的误差时，其误差也通过仿真器给出。

1.2.1 陀螺仿真器的数学模型［5－6］

职业教育主要培养面向企业一线具有较强实践性和职业性的技能型人才，要求教师不仅具备专业理论知识，还需要有一定的实践能力。近年来，随着我国社会经济发展，产业结构调整等新情况的出现，职业教育师资队伍总量不足、培养机制不完善等，因此，有必要分析职院校“双师型”教师队伍建设存在的问题以及提出解决路径。

理想角速率陀螺仪测量的是机体坐标系（b系）相对与惯性坐标系（i系）的转动角速率在机体坐标系中的投影ϖ。从飞行轨迹数据中，可以得到机体坐标系相对于导航坐标系（n系）的转动角速率在机体坐标系中的投影。通过飞行轨迹数据中的水平速度、纬度、高度可以计算出导航坐标系相对于惯性坐标系的转动角速率在导航坐标系中的投影，通过姿态角算出从导航坐标系到机体坐标系之间的转换矩阵乘上转换矩阵得到相加，得到陀螺仪模型的理想输出。

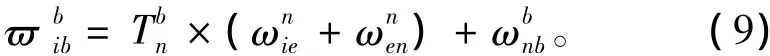
完整的陀螺模型包括理想输出量、随机误差量（随机常值误差、白噪声误差、一阶马尔可夫过程误差）、刻度因子误差，用数学公式表示为:

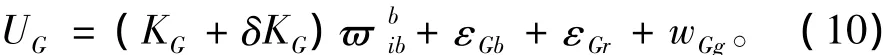
式中:UG为完整陀螺模型的输出;KG为刻度因子; δKG为刻度因子误差;为陀螺模型理想输出;εGb为陀螺随机常数误差;εGr为陀螺一阶马尔可夫过程误差;wGg为陀螺白噪声误差。

1.2.2 加速度计仿真器的数学模型［7－8］

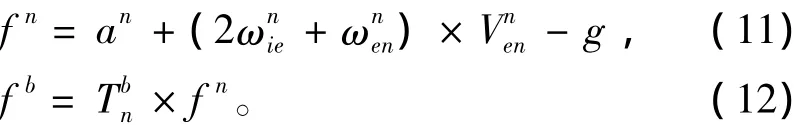
完整的加速度计模型包括理想输出量、随机误差量（随机常值误差、白噪声误差、一阶马尔可夫过程误差）、刻度因子误差，可用数学公式表示为:

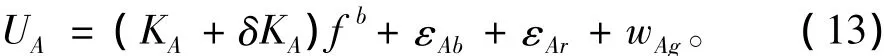
1.3 导航计算机仿真器

导航计算机的仿真可以根据系统对计算机的要求及现有的机载计算机的性能进行。在仿真中可以对计算精度、计算时间、计算字长及单精度与双精度计算等方面取得必要的数据，以便选择合适的机载计算机及计算机算法。

1.4 误差处理器

由导航计算机仿真器计算出的带误差的导航参数与飞行轨迹发生器产生的精确导航参数进行比较，得出计算的位置、姿态、地速、高度等参数的导航误差。可以通过误差曲线图分析仿真结果是否正确，完成全部的捷联系统数字仿真器工作。

利用C语言设计的捷联惯导系统仿真器已在微机上实现。仿真环境是在静态条件下，选择地理坐标系为数字平台。在对飞行轨迹数据仿真的算法公式中:θ，λ和h分别为纬度、经度和高度;φ，γ和ψ分别为俯仰角、横滚角和航向角。仿真过程中，式（1）和式（3）所涉及参数设定的缺省值为［9］:

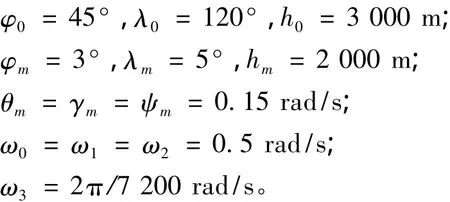
飞机位置、姿态角的误差曲线图分别如图2～图4所示。

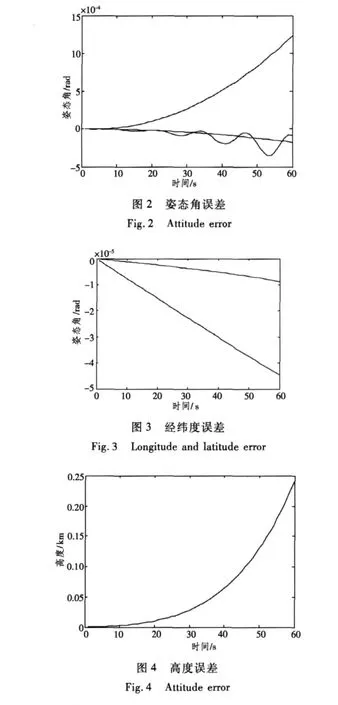
仿真结果表明，捷联惯导仿真器工作正常，惯导的位置误差、姿态误差随时间积累，长时间工作后惯导精度无法满足导航或制导的精度要求。以上仿真误差曲线是在陀螺仪与加速度计没有误差，也没有初始对准误差的理想条件下生成的捷联惯导仿真误差曲线，产生误差的主要因素是计算误差。可以看出，随着时间的增长，误差也在呈发散趋势增长。因此，必须采取有效手段，对惯导系统进行修正，以提高导航精度。

2 结语

本文所设计的捷联惯导系统仿真器利用面向对象的思想进行模块分解，具有很强的扩展性。该仿真器大大缩短了从理论方案到实际应用之间的距离，为工程应用提供了一种全面观察捷联系统在不同应用条件下精度、性能的强有力的工具。结合不同的使用环境，可以对其中具体的模块进行相应的重新设计。比如轨迹发生器仿真模块、惯性敏感元件误差模块都可以依据系统具体的工作环境，对其中的各种参数或公式进行重新选择，从而达到更加真实的仿真效果。

［1］陈哲．捷联惯导系统原理［M］．北京:宇航出版社，1986．206－211．

［2］李丽娟，王琪，罗超．VC环境下捷联惯导模拟器的开发［J］．应用科技，2006，33（3）:46－49．

［3］刘柱，高伟，曹洁．捷联惯导系统仿真器的设计［J］．应用科技，2004，31（7）:40－42．

［4］LEE J G，PACK H W．Multiposition alignment of strapdown inertial navigation system［J］．IEEE Transactions on Aerospace and Electronic Systems，1993，29（4）:1323－1328．

［5］GAI E．The century of inertial navigation technology［J］．Aerospace Conference Proceedings，2000，11（3）:59－60．

［6］LOVREN N，PIEPER J K A．Strapdown inertial navigation system for flat-earch model［J］．IEEE Transaction on Aerospace and Electronic Systems，1997，33（1）:214－224．

［7］吴小兰．易于实现的捷联式惯性导航系统仿真［J］．弹箭与制导学报，2006，26（4）:89－91．

［8］黄金明，王立文，郑淑涛．飞行模拟器综合导航系统建模与仿真［J］．系统仿真学报，2006，18（s2）:665－668．

［9］赵玉霞．捷联惯导系统仿真算法的研究及其实现［D］．大连:大连理工大学，2005．