叠合板用预制预应力混凝土带肋薄板的刚度试验研究与计算方法*

吴方伯,黄海林,陈 伟,周绪红

(湖南大学 土木工程学院,湖南 长沙 410082)

叠合板用预制预应力混凝土带肋薄板的刚度试验研究与计算方法*

吴方伯†,黄海林,陈 伟,周绪红

(湖南大学 土木工程学院,湖南 长沙 410082)

为探讨新型预制预应力薄板(带肋且肋上设有孔洞,截面刚度呈阶梯形变化)的短期刚度与弯曲挠度的计算方法,进行了10块矩形肋预制预应力带肋薄板、2块T形肋预制预应力带肋薄板静载试验,得到了跨中荷载-挠度曲线.理论推导得到考虑肋上孔洞分布及肋端缺口的预制预应力带肋薄板弯曲挠度通用公式以及等效刚度公式,便于编制计算机程序进行计算.对比分析了基于等效刚度公式计算及试验得到的跨中荷载-挠度曲线,结果表明:均布荷载作用下两端简支预制预应力带肋薄板短期刚度可按0.85倍等效刚度计算.

叠合板;带肋薄板;预制混凝土;弯曲挠度;阶梯形刚度

混凝土叠合板是在底部采用预制板件,上部叠合现浇混凝土,二者共同形成整体的结构.我国从20世纪50年代开始生产预制混凝土实心板件,针对混凝土叠合结构二次受力特性进行了大量研究[1-2].而国外的研究主要集中在叠合面的抗剪强度、抗剪连接,叠合面上下两部分的收缩微差造成的附加内力和变形,预制构件对后浇混凝土极限变形的抑制以及抗裂度和挠度的计算方法等问题,大部分研究是针对一次受力叠合结构,未能反映混凝土叠合楼板在无支撑施工条件下的二次受力特点[3].20世纪90年代,由于高强材料的应用,钢筋已从非预应力发展到预应力,受力主筋也从冷加工钢筋发展到采用高强、低松弛的钢丝、钢绞线,混凝土也向轻质、高强方向发展.针对采用新型材料的混凝土叠合板结构性能,国内外学者进行了大量研究[4-9],但研究较多的还是针对采用实心平板的混凝土叠合结构.

由于叠合板用预制预应力混凝土实心平板为不带肋预制板件,在运输及施工过程中易折断,预应力反拱值难以控制,施工过程中需设支撑、施工工艺复杂.我国现行国家标准《叠合板用预应力混凝土底板》GB/T 16727—2007、国家建筑标准设计图集《预应力混凝土叠合板》06SG439中叠合板预制部分均为平板,施工时需设置支撑,不宜双向配筋,自重大,降低了这种结构的经济效果,影响了其推广使用.为此,国内学者提出预制预应力带肋薄板,并针对带肋式混凝土叠合板进行了大量研究[10-12].将预制混凝土实心平板改进为带肋的预制薄板,提高了薄板的刚度和承载力,增加了预制薄板与叠合层的粘结力,但由于只能单向配筋,垂直于底板板长方向的抗裂性不好,且荷载采用单向板传力模式,计算模型不合理.

针对上述问题,文献[13]提出以预制预应力带肋薄板为底板,在板肋预留孔中布设横向穿孔钢筋及在底板拼缝处布置折线形抗裂钢筋,再浇注混凝土叠合层形成的双向配筋楼板.预制预应力带肋薄板(以下简称预制薄板)带肋且肋上预留矩形孔洞,如图1所示,截面刚度呈阶梯形变化,其短期刚度及弯曲挠度的计算成为该新型叠合板二次受力分析要解决的重要问题.本文通过10块矩形肋、2块T形肋预制薄板静载试验,得到了跨中荷载-挠度曲线;通过理论分析推导了预制薄板弯曲挠度的通用公式与考虑肋上孔洞分布及肋端缺口的等效刚度公式,为深入开展该新型叠合板二次受力性能的研究提供了依据.

1 试验研究

1.1 试件设计与制作

共设计制作了12块预制薄板试件,其中10块为矩形肋预制薄板,适用跨度为2.4～6.0 m,2块为T形肋预制薄板,适用跨度为6.0～9.0m,试件设计见图2.预制薄板试件基本参数及混凝土性能指标见表1.预制薄板试件的底板配预应力筋,预应力筋受拉截面中心距板底17.5mm,在矩形肋内、T形肋翼缘内配普通钢筋,钢筋截面重心到矩形肋或翼缘上边缘距离为20 mm,钢筋配置情况及力学性能见表2.

图1 预制薄板Fig.1 Precast p restressed ribbed panels

表1 预制薄板试件基本参数Tab.1 Basic parameters of precast ribbed panels

表2 钢筋配置情况及力学性能Tab.2 M echanical properties of reinforcing steels

1.2 试验装置与加载方案

试验采用红砖及水泥袋进行加载.在预制薄板试件跨中和支座处安装百分表,以测量跨中挠度,试验加载装置及挠度测点布置见图3.试验前先计算出预制薄板试件的开裂荷载和极限荷载,以便试验过程中进行控制和比较.预加载取计算开裂荷载的20%.正式加载中,达到计算开裂荷载90%前,每级荷载取计算开裂荷载的20%;此后,每级荷载取计算开裂荷载的5%.开裂后,加载达到计算极限荷载90%前,每级荷载取计算开裂荷载的10%;此后,取计算开裂荷载的5%.开裂后,加载达到计算极限荷载90%前,每级荷载取计算开裂荷载的10%;此后,每级荷载取计算开裂荷载的5%.每级荷载加载完毕后停留 10 m in.当试件跨中挠度超过跨度的1/50,即认为板件破坏,停止加载.

图2 预制薄板试件设计图Fig.2 Design of precast panels

1.3 试验结果及分析

试验测得的矩形肋预制薄板跨中荷载-挠度曲线如图4所示,所有试件在加载到承载力极限状态时挠度尚未达到跨度的1/50,试件抗弯刚度较大.预应力筋与混凝土之间的粘结锚固性能很好,最后由于钢筋达到极限抗拉强度而破坏.试验测得的T形肋预制薄板跨中荷载-挠度曲线如图5所示,开裂前每级荷载产生的挠度较小;开裂时,跨中首先出现数道细密裂缝,随着荷载的增加,板件挠度变形及裂缝不断增加,最后由于板件挠度达到跨度的1/50而停止加载.破坏时试件弯曲变形特征明显,最大裂缝宽度0.3 mm;大部分裂缝向上延伸至板件底板上表面,但T形肋上未发现可见裂缝,板件受压区混凝土完好,无压碎,预应力钢筋无滑移现象.卸载后,板件基本回复至原来位置,残余变形15 mm.

图3 试验加载装置及挠度测点布置Fig.3 Test setup andmeasured points

2 理论分析

工程实际中常遇到阶梯形变截面梁、板,求其复杂荷载作用下的变形多采用近似的数值解法.文献[14]给出阶梯形变截面梁第n段变形的通用方程,需计算各段端点的转角多项式和挠度多项式的值.文献[15]利用广义函数研究了截面呈阶梯形变化的梁板弯曲问题,直接导出了挠度通用公式.文献[16]采用直接积分法求解变惯性矩梁变形,要确定若干积分常数.文献[17]利用Heaviside函数,将任意变刚度化为阶梯刚度,导出了任意变刚度梁变形的一种通用方程的微分形式和积分形式.本文在已有变截面梁、板弯曲挠度理论研究成果基础上,结合预制薄板特点,推导得到考虑肋上孔洞分布及肋端缺口的预制薄板弯曲挠度通用公式,并利用M atlab7.1编制计算机程序进行计算.结合工程实际,通过简化分析推导得到均布荷载作用下两端简支预制薄板等效刚度公式.

图5 T形肋预制薄板跨中荷载-挠度曲线Fig.5 Load-deflection curves o f T-shaped rib precast panels

2.1 预制薄板的刚度函数

利用单位阶梯函数:

式中常数 α≥0,预制薄板的抗弯刚度 D(x)= EI(x)可表示为阶梯形式,如图6所示.根据预制薄板肋上孔洞分布及肋端缺口将其划分为2 n+3段(n为肋上预留孔数,n≥10),其中第r段的端点号为(r,r+1),dr为第r点(r=1,2,…,2 n+3)的x坐标,Dr为第r段抗弯刚度,dr(r=2,3,…,2 n +3)截面为预制薄板抗弯刚度函数D(x)的跳跃间断点,该点左右极限取:

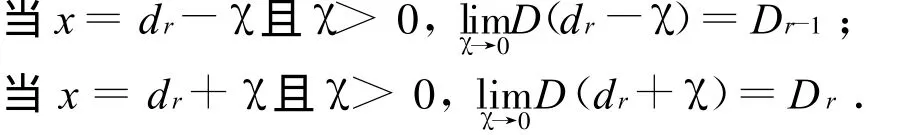
则预制薄板任意截面的刚度函数表示为:

2.2 预制薄板内力的通用方程

在图6所示工程常见荷载作用下(集中荷载、任意线性分布荷载、集中力偶),利用单位阶梯函数与Dirac delta函数δ的性质[18],预制薄板荷载密度函数 f(x)表示为:

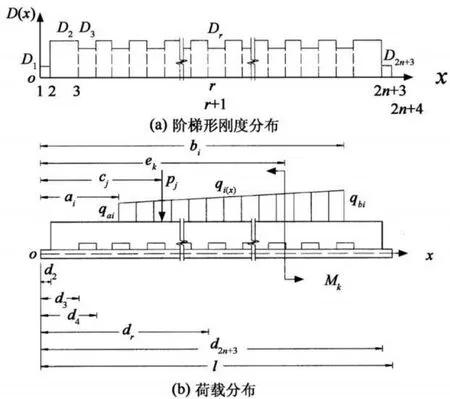
图6 预制薄板试件荷载、阶梯形刚度分布Fig.6 Load and stepped rigidity distribution of p recast panels

线性分布荷载函数为:

式中:qi(x)为第i个线性分布荷载,qai,qbi为第i个线性分布荷载区间[ai,bi]两端给定值.

将式(4)代入式(3),简化得到:

将式(5)代入式(6),并将左端支座截面(x= 0)弯矩与剪力记入外载中,得含单位阶梯函数及δ函数的常系数微分方程:

采用拉普拉斯变换进行求解,得到预制薄板内力的通用方程:

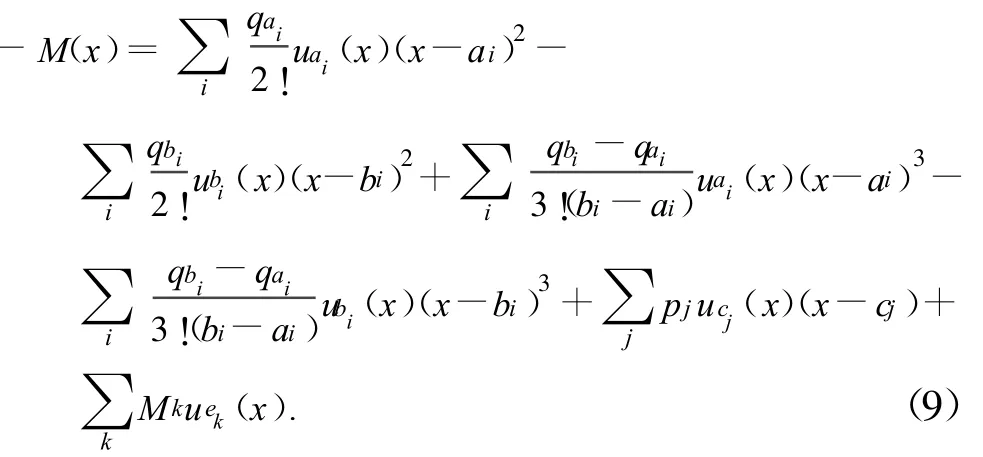
2.3 预制薄板变形的通用方程

一般情况下,预制薄板弹性小变形挠曲线可由式(10)求得:

将式(2)、式(9)代入式(10)得预制薄板变形的通用方程:

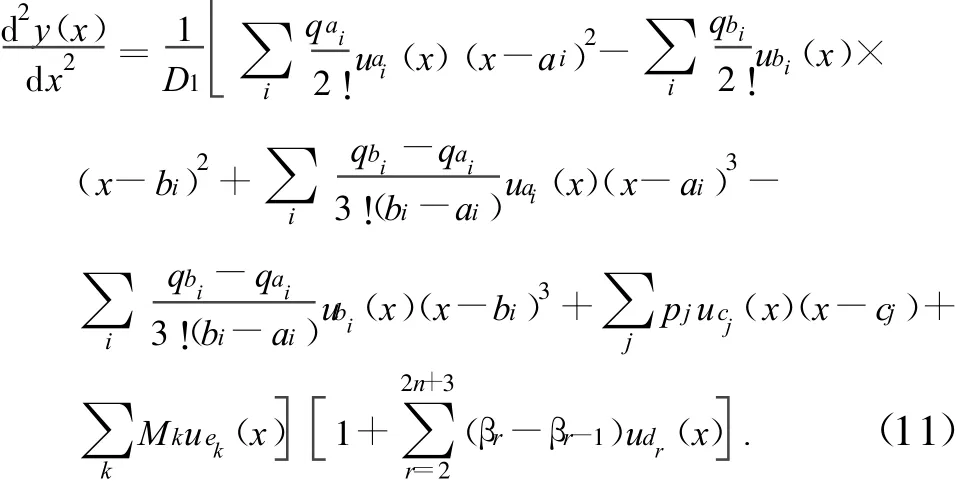
本文预制薄板试件两端简支,采用均布荷载进行加载,有:

将其代入式(11),采用拉普拉斯正反变换求解得到均布荷载作用下两端简支预制薄板弯曲挠度的通用公式:

式中:y0,θ0为左端支座截面(x=0)的挠度和转角, yq(x),yp(x)分别为均布荷载、集中荷载单独作用下不考虑初始值的变形,具体表达式如下:

定义D e=λD 1,D e,λ分别为预制薄板等效刚度、等效刚度系数,则有:

3 理论分析与试验结果的对比

《混凝土结构设计规范》GB 50010-2002规定:对于要求不出现裂缝的预应力混凝土受弯构件短期刚度取0.85Ec I0,式中,Ec I0为预制构件理论弹性刚度,0.85为理论弹性刚度的折减系数,Ec为预制构件混凝土弹性模量,I0为换算截面惯性矩.

由于预制薄板肋上孔洞及肋端缺口的存在,截面刚度呈阶梯形变化,实际工程中若不考虑肋上孔洞及肋端缺口对板件刚度的影响,则计算出的刚度偏大,计算模型与实际受力情况不符.为此,本文考虑了肋上孔洞及肋端缺口对预制薄板刚度的影响,根据式(25),利用M atlab7.1编制了计算机程序进行了计算,为验证式(25)计算公式的准确性,将计算结果与试验结果进行了对比,如图7所示.由图7可知,当预制薄板开裂前,基本处于弹性阶段,荷载-挠度曲线近似呈直线关系,但按De计算的跨中挠度小于试验值,可见预制薄板开裂前的刚度D e是板件刚度的上限值,实际工程设计应对D e取一定的折减系数,本文按0.85De计算的跨中挠度稍大于试验值,且与试验结果较为接近;当预制薄板板底出现第一条裂缝,跨中荷载-挠度即出现明显转折点,随着荷载加大,板底裂缝增多,预制薄板刚度逐渐减小,按式(25)计算的跨中挠度与试验结果偏离逐渐增大.因此对于开裂前的预制薄板,取0.85De作为弹性刚度是偏安全的,可用于实际工程设计.

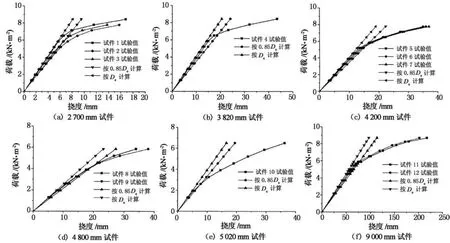
图7 跨中荷载-挠度曲线试验结果与理论计算结果对比Fig.7 Comparison of load-def lection curves inm id-span between experimental and theoretical result

4 结 语

本文分析了截面刚度呈阶梯形变化的预制薄板跨中挠度计算方法.通过简化分析,建立了均布荷载作用下两端简支预制薄板的等效刚度公式,根据式(25)计算了均布荷载作用下两端简支预制薄板的跨中挠度.通过对理论计算结果和试验结果的分析和比较,对于开裂之前处于弹性工作阶段的预制薄板,可得出如下结论:

1)用本文提出的考虑肋上孔洞分布及肋端缺口的预制薄板弯曲挠度通用公式,可精确求解任意截面的弯曲挠度,同时便于编制计算机程序进行计算.

2)不考虑预制薄板肋上孔洞及肋端缺口对板件刚度的影响,则计算的刚度偏大,计算结果不符合这种新型薄板的实际受力情况;考虑肋上孔洞分布及肋端缺口对预制薄板刚度的影响,计算精度明显提高,且与试验值吻合较好,可供工程设计参考.

3)对于要求不出现裂缝的均布荷载作用下两端简支预制薄板短期弯曲刚度,本文建议取0.85De进行实际工程设计;通过引入预制薄板等效刚度De,建立了与规范统一的弹性刚度形式.

[1] 过镇海.常温和高温下混凝土材料和构件的力学性能[M].北京:清华大学出版社,2006:63-89.

GUO Zhen-hai.Concretematerials and components performance under normal temperature and high temperature[M].Beijing:Tsinghua University Press,2006:63-89.(In Chinese)

[2] 周旺华.现代混凝土叠合结构[M].北京:中国建筑工业出版社, 1998:12-14.

ZHOUWang-hua.Modern concrete compositestructures[M].Beijing:China Architecture&Building Press,1998:12-14.(In Chinese)

[3] PC J.Composite structuremethods[M].New York:McGraw-Hill Book Company Inc,1976.

[4] 刘翠兰,祁学仁.部分预应力陶粒混凝土叠合板的试验研究[J].建筑结构学报,1992,13(4):12-20.

LIU Cui-lan,QI Xue-ren.Experimental study on partially prestressed ceramsite concrete composite slabs[J].Journal of Building Structures,1992,13(4):12-20.(In Chinese)

[5] 徐吉恩,骆艳斌.钢纤维混凝土预应力连续叠合板变形研究[J].武汉水利电力大学(宜昌)学报,2000,22(1):11-15.

XU Ji-en,LUO Yan-bin.Experimental study on deformation of SFRC prestressed composite plates[J].J of Univ of Hydr&Elec Eng/Yichang,2000,22(1):11-15.(In Chinese)

[6] 侯建国,贺采旭.高强刻痕钢丝预应力连续叠合板试验研究[J].建筑结构,1991,(10):43-48.

HOU Jian-guo,HECai-xu.Experimentalstudy on prestressed continuous composite slab reinforced with high tensile indented steel wires[J].Building Structure,1991,(10):43-48.(In Chinese)

[7] 杨万庆.螺旋肋筋预应力叠合板的受力性能研究[J].工程力学, 2001,(A 02):268-272.

YANGWan-qing.Mechanical properties study on prestressed concrete composite floor reinforced with spiral ribbed steel wires[J]. Engineering Mechanics,2001,(A02):268-272.(In Chinese)

[8] 廖莎,马远荣.活性粉末混凝土(RPC)预应力叠合梁受弯性能研究[J].湖南大学学报:自然科学版,2005,32(1):57-62.

LIAO Sha,MA Yuan-rong.Study on bending performance of reactive powder concrete prestressed composite beams[J].Journal of Hunan University:Natural Sciences,2005,32(1):57-62.(InChinese)

[9] ROBERTS-WOLLMANN C L,GUIROLA M,Easterling W S. Strength and performance of fiber-reinforced concrete composite slabs [J].Journalof Structural Engineering,2004,130(3):520-528.

[10]岳建伟,鲍鹏,徐书耀.新型叠合板的理论分析和实验研究[J].河南大学学报:自然科学版,2002,32(1):87-90.

YUE Jian-wei,BAO Peng,XU Shu-yao.Theoretical analysis and experimental study ofa new composite slab[J].Journalof Henan U-niversity:Natural Science,2002,32(1):87-90.(In Chinese)

[11]徐天爽,徐有邻.双向叠合板拼缝传力性能的试验研究[J].建筑科学,2003,19(6):11-14.

XU Tian-shuang,XU You-lin.Experimental study on transm ission propertiesof joints between superposed slabs[J].Building Science, 2003,19(06):11-14(In Chinese)

[12]刘汉朝,蒋青青.倒“T”形叠合简支板的试验研究[J].中南大学学报:自然科学版,2004,35(1):147-150.

LIU Han-chao,JIANG Qing-qing.Experiment of inverted“T” simply supported composite slab[J].JCent South Univ:Natural Science,2004,35(1):147-150.(In Chinese)

[13]周绪红,张微伟,吴方伯,等.预应力混凝土四边简支双向叠合板的设计方法[J].建筑科学与工程学报,2006,23(4):54-57.

ZHOU Xu-hong,ZHANG Wei-wei,WU Fang-bo,et al.Design method of prestressed concretesimply supported on four sidesof tw ow ay composite slab[J].Journal of A rchitecture and Civil Engineering,2006,23(4):54-57.(In Chinese)

[14]李建成.计算变截面梁变形的通用方程[J].力学与实践,1988, 10(1):37-39.

LI Jian-cheng.A general equation of deformation in variable crosssection beams[J].Mechanics in Engineering,1988,10(1):37-39. (In Chinese)

[15]章青.变截面梁板弯曲问题的一般解答[J].应用力学学报,1990, 7(3):94-98.

ZHANG Qing.General solution of the bending problem for variable cross-section beams and slabs[J].Chinese Journal of Applied Mechanics,1990,7(3):94-98.(In Chinese)

[16]李银山,杨椎阳.变惯矩梁变形的函数解[J].力学与实践,1992, 14(2):55-58.

LI Yin-shan,YANG Chui-yang.Functionmethod of deformation in variable inertiamoment beams[J].Mechanics in Engineering,1992, 14(2):55-58.(In Chinese)

[17]朱先奎.变截面梁弯曲挠度的通用公式及其应用[J].武汉水利电力大学学报,1993,26(5):562-568.

ZHUXian-kui.A general formula of deflection in variable cross-section beamsand itsapplication[J].JournalofWuhan Univ of Hydr& Elec Engineering,1993,26(5):562-568.(In Chinese)

[18]TYN MYINT-U.Partialdifferentialequationsofmathematicalphysics[M].New York:Elsevier Science&Technology Books,1980: 319-341.

Experimental Study and Calcu lating M ethods on Bending Rigidity of Precast Prestressed Concrete Ribbed Panels for Composite Slabs

WU Fang-bo†,HUANG Hai-lin,CHEN Wei,ZHOU Xu-hong

(College of Civil Engineering,Hunan Univ,Changsha,Hunan 410082,China)

In order to discuss the calculating methods of short term rigidity and bending deflection,ten precast prestressed concrete ribbed panels(PPCRP)with rectangular rib and two PPCRPw ith T-shaped rib were tested,and the load-deflection curves were obtained.The general formula of bending deflection taking into account the distribution of preformed holes in the rib and equivalent rigidity form ula for PPCRP were deduced.The contrastanalysis of load-deflection curves obtained from equivalent rigidity formula and test resu lt show that short term rigidity of sim ply supported PPCRP under uniform ly distributed load can be calculated at 0.85 times as equivalent rigidity.

com posite slabs;ribbed panels;precast concrete;bending deflection;stepped rigidity

TU 375.2

A

1674-2974(2011)04-0001-07 *

2010-09-20

国家自然科学基金资助项目(50978090);湖南大学研究生创新基金资助项目(CX2010B143);湖南大学博士学位论文选题资助计划项目

吴方伯(1959-),男,湖南长沙人,湖南大学教授,博士生导师

†通讯联系人,E-mail:w fbprof@163.com