大跨屋盖风压场的本征正交分解与重构适应性研究＊

李寿科，李寿英，陈政清，黄 韬

（湖南大学风工程试验研究中心，湖南长沙 410082）

大跨屋盖风压场的本征正交分解与重构适应性研究＊

李寿科，李寿英†，陈政清，黄 韬

（湖南大学风工程试验研究中心，湖南长沙 410082）

对3类典型屋盖（封闭式方形平屋盖、封闭式曲面屋盖和开合式曲面屋盖）进行了刚性模型风洞测压试验，分析了典型风向角下的平均及脉动风压系数分布.利用POD方法对3类屋盖的风压场进行了分解，并对平屋盖风压场进行了POD重建.结果表明：斜风向封闭式平屋盖的POD分解性能最优，开合式曲面屋盖次之，封闭式曲面屋盖最差.3类屋盖的第1阶POD特征向量均反映平均风压系数分布，45°风向角下封闭式平屋盖的第2阶POD模态可以较好地反映锥形涡分量，而其他类型屋盖的高阶特征向量则反映风压场的局部分布.风压场的POD重建具有不平衡的性能，对于相同测点，模态数越多，其重建效果越好.对于不同测点相同模态数，测点脉动风压系数越大，其风压重建效果越好.

风洞；封闭式平屋盖；封闭式曲面屋盖；开合式曲面屋盖；本征正交分解

大跨空间屋盖由于其形状各异，周围流场的分离、再附以及漩涡脱落等诸多因素导致其表面风压分布非常复杂，一般情况下，其风荷载采用风洞试验来确定.风洞试验受到同步测压通道数的限制，因此，研究者将本征正交分解（Proper Orthogonal Decomposition，POD）方法引入风工程领域，用来描述结构表面的风压场.POD方法是一种基于相关矩阵或协方差矩阵的特征值问题分析的随机场表示方法，是一种时空分离的分析方法，可把风压场分解为与时间相关的主坐标和与空间相关的特征向量组合.国外学者首先进行了这方面的研究工作，Bienkiewicz等［1］采用POD方法对一低矮建筑边角区域的面平均压力、整个屋面以及立墙测点风压进行了风压场重建研究，并讨论了前几阶本征模态的物理意义.Ho等［2］利用POD方法研究了双坡屋面风压场，并分析了POD方法简化风压场的精度.Jeong等［3］对TTU刚性模型风压场进行了POD分解，并采用自回归模型研究了其时间主坐标，从而进一步对风压场进行简化.Jeong等［4］对TTU模型的屋盖风压进行了均匀布点和非均匀布点的POD分解，提出了一种通过面积加权来实现非均匀布点POD分解的方法.POD方法还可用于风压预测，李方慧等［5］等采用POD方法对双坡屋面未布置测点处的风压进行预测，结果表明风压预测可以提高风压场的分辨率.李元齐等［6］研究了POD方法在曲面模型风压场重建中的应用，比较了球面和柱面模型风压场的POD重建特点.

以往的研究主要集中于一些特殊形式的屋盖，如平屋盖，球面屋盖和柱面屋盖等，而对工程实际中屋盖却鲜有研究.为使POD方法能用于工程实际，本文选取实际工程中的封闭式方形平屋盖、封闭式曲面屋盖和开合式曲面屋盖进行刚性模型测压风洞试验，采用POD方法对上述3种类型屋盖的风压场进行POD分解，通过对特征值和特征向量的比较分析，研究POD方法对上述3种屋盖的适应性问题.另外，以往对于POD重建性能的研究也较少，本文基于POD方法对封闭式方形平屋盖风压场进行重建，研究风压场POD方法重建性能.

1 基本理论

风压场POD分解的目的在于找到一组基函数Φ＝［Φ1，Φ2，…，ΦN］，使N个测点构成的风压系数场Cp（t）＝｛Cp1（t），Cp2（t），…，CpN（t）｝在基函数上的投影为最大，此时基函数与风压系数场最相关.POD分解提供了一种可仅使用较少的本征模态描述复杂的随机过程的途径，基函数Φj需满足［4，7］：

式中：RP为N个测点风压系数时程的协方差矩阵；λj为第j阶特征值；Φj为第j阶模态向量；N为测点总数；W为N个测点所属面积的对角矩阵，W＝diag（W1，W2，…，WN）.若各测点代表面积相等，即W1＝W2＝…＝WN＝ΔA，则式（1）可写为：

式（10）表明所有特征模态对特征值进行加权求和为风压场的均方能量，故每一阶模态所占能量百分比可用特征值比来表示.

风压系数场的能量可能集中在少数的前NR阶本征模态，NR＜N，因而可以用时间主坐标和本征向量表示压缩的风压系数场.风压系数场时程可采用前NR阶本征模态近似表示为：

2 工程背景

选取3种不同形式的屋盖结构进行刚性模型同步测压风洞试验.

第1种为封闭式方形平屋盖.其建筑尺寸为长100 m×宽100 m×高30 m，模型缩尺比1∶200，试验模型照片如图1（a）所示，测点布置在上表面，成10行10列排列，共100个测点，如图2（a）所示.第2种为封闭式曲面屋盖，该屋盖为具有椭圆形平面投影的屋盖结构，长轴135 m、短轴116 m，屋盖最高点标高为49 m，模型缩尺比1∶200，试验模型照片如图1（b）所示，测点布置在屋盖上表面，共165个，如图2（b）所示.第3种为开合式曲面屋盖，该屋盖包括固定屋盖和活动屋盖2部分，固定屋盖平面投影为椭圆形，长轴270 m、短轴220 m，屋盖最高点标高为60 m，活动屋盖位于主屋盖的中心处，长106 m、宽80 m，活动屋盖可以开启和关闭，模型缩尺比为1∶300，试验模型照片如图1（c）所示，采用双面测点，屋盖上、下表面测点一一对应，共408个，如图2（c）所示.

试验在湖南大学HD-2边界层风洞中进行，风场类型为B类，转盘中心处的平均风速剖面、湍流度剖面及顺风向风功率谱详见文献［8］.采样时间20 s，采样频率330 Hz.风向角间隔15°，共24个风向角，各模型的风向角定义见图2.限于篇幅，主要对上述3个模型典型的风向角进行研究.其中，方形平屋盖为0°和45°风向角；封闭式曲面屋盖为0°风向角，开合式曲面屋盖为活动屋盖开启工况下的180°风向角.

图1 试验模型在风洞中的照片Fig.1 Typical view of model test in BLWT

3 试验结果

平均风压系数C¯p和脉动风压系数Cp＇定义为：

式中：¯p和σp分别为各测点所测得风压时程的平均值和根方差值；qH为3个模型各自屋盖顶部参考高度处的总压，对每个模型，参考高度取为屋盖最高点处.

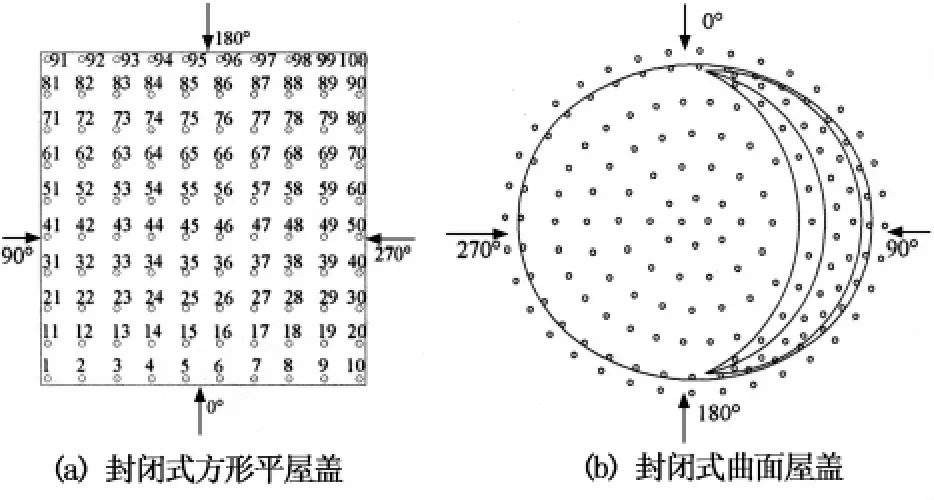
图2 刚性模型风洞试验测点布置图Fig.2 Pressure port locations

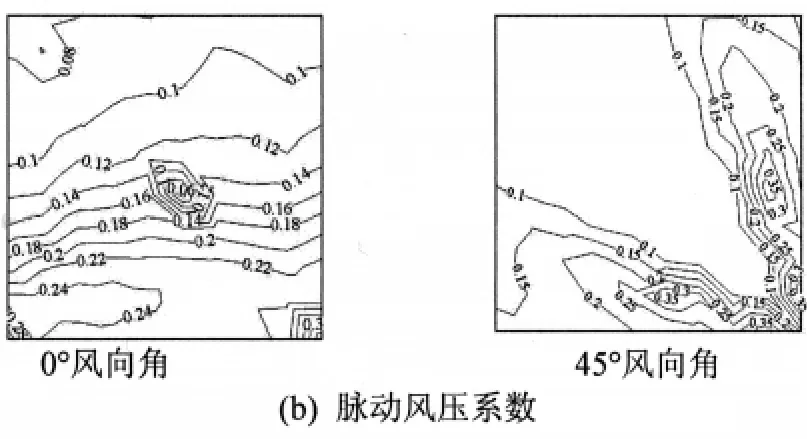
图3 平屋盖模型平均及脉动风压系数等值线（0°和45°风向角）Fig.3 Mean and fluctuating wind pressure coefficients distribution for flat roof（wind angle of 0°and 45°）

图3为封闭式方形平屋盖在0°和45°风向角的平均及脉动风压系数等值线图.由图3可知，平屋盖表面风压以负压为主，分布对称性较好，其0°风向角时屋盖迎风前缘气流分离明显，平均风压系数最大达到－0.9，脉动风压系数最大达到0.24；斜风向45°时气流分离形成明显的锥形涡，从而使迎风角点处的平均风压系数最大达到－1.6，且脉动风压系数达到0.35.图4为封闭式曲面屋盖在0°风向角下的平均及脉动风压系数等值线图.由图4可知，屋盖表面以负压分布为主，气流在迎风前缘和屋盖突起的两端分离较为明显.图5为开合式曲面屋盖在活动屋盖开启时180°风向角下的固定屋盖净平均及脉动风压系数等值线图.由图5可知，屋盖净平均风压系数在0.3～－0.3内变化，迎风前缘来流分离沿着屋盖边缘形成小区域带状的负压分布；而大部分的迎风区域为正压分布（0～0.3）；屋盖的背风面呈负压分布；固定屋盖净脉动风压系数在0.04～0.24内变化，最大值0.24出现屋顶开口的下风侧，此处来流分离最为强烈.比较图3，图4和图5可以明显看出，开合屋盖由于屋顶开启其平均风压系数（绝对值）要明显小于封闭式屋盖，但其脉动风压系数则略有增加.

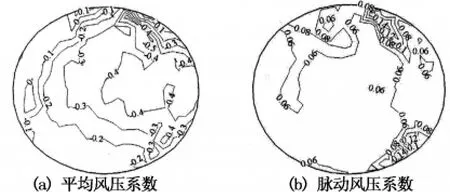
图4 封闭式曲面屋盖的平均及脉动风压系数等值线（0°风向角）Fig.4 Mean and fluctuating wind pressure coefficients distribution for closed curved roof（wind angle of 0°）

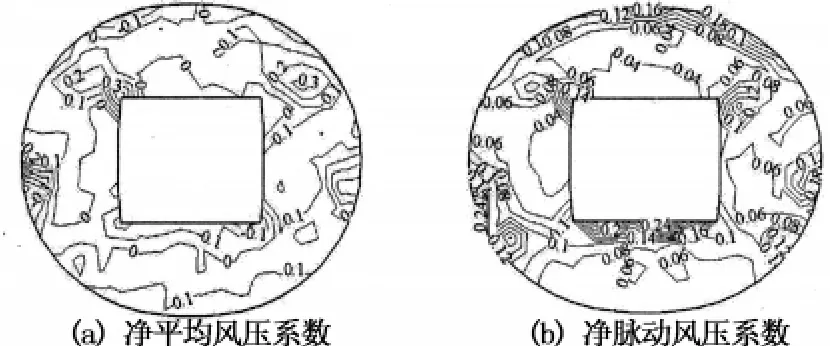
图5 开合式曲面屋盖净平均及脉动风压系数等值线（180°风向角）Fig.5 Mean and fluctuating wind pressure coefficients distribution for retractable roof（wind angle of 180°）

4 POD分解

4.1 特征值

表1给出了0°和45°风向角下的封闭式方形平屋盖风压系数场的POD分解特征值.不同风向角下风压系数场的气流分离机制不同，致使其风压系数场POD分解后的特征值不相同，各阶模态的特征值在整个风压系数场中所占能量百分比亦不同.从表1中可以看出，由一对锥形涡控制的45°风向角的1阶模态所占的能量累计为21.74%，而0°风向角的1阶模态所占的能量累计为18.84%.如需POD分解能量累计到90%以上，对于0°风向角，前54阶模态的能量累积达到90%，而对于45°风向角，仅需35阶模态的能量累积即可达到90%.因此，对于方形平屋盖，特征湍流锥形涡45°风向角的POD分解性能要明显优于0°风向角.

表2给出了封闭式曲面屋盖（0°风向角）和开合式曲面屋盖（180°风向角）在典型风向角下风压系数场POD分解的特征值.由表2可知，封闭式曲面屋盖前71阶模态的能量累积达到90%，占总模态数的43%；而开合式曲面屋盖前78阶模态的能量累积达到90%，占总模态数的38%.由表2可以看出，对于同属曲面屋盖形式的封闭式曲面屋盖和开合式屋盖，虽然封闭式曲面屋盖风压系数场的低阶模态（1～4阶）含有更多能量，但高阶时能量离散程度较大，故采用POD方法对风压数据进行压缩时，开合式曲面屋盖数据压缩性能要优于封闭式曲面屋盖.

表1 封闭式方形平屋盖风压系数场POD分解的特征值及其能量累积百分比Tab.1 Contribution proportion of each mode from POD for closed flat roof

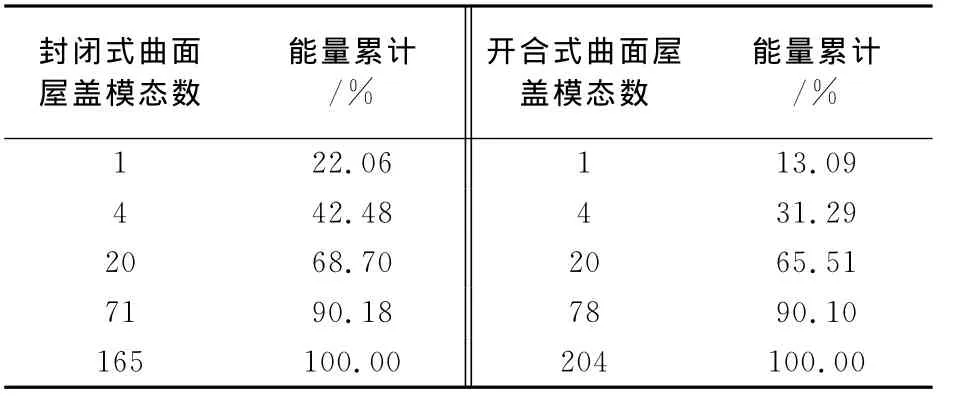
表2 封闭式曲面屋盖和开合式曲面屋盖POD分解的特征值能量累积百分比Tab.2 Contribution proportion of each mode from POD for closed curved roof and retractable roof

对比表1和表2可知，封闭式方形平屋盖的POD分解性能最优，其次为开合式曲面屋盖，封闭式曲面屋盖的POD分解性能最差.

4.2 特征向量

图6给出了0°和45°风向角下封闭式方形平屋盖风压系数场POD分解的前4阶特征向量的等高线图.比较图6（a）与图3（a）可知，POD分解的第1阶模态与表面平均风压系数具有相似的分布特征，随着模态阶数的增加，特征向量与风压系数总体分布的相似性越差，高阶模态则仅反映风场系数场的局部特征，这与文献［6］的结论相同.45°风向角下（图6（b）），屋盖风压由一对锥形涡控制，第1阶特征向量反映平均风压系数分布，特征向量最大值0.04出现在屋面边缘，位置与平均风压系数最大值出现位置相同.第2阶特征向量表现出明显锥形涡特征，左右两个锥形涡正负压交替出现，且能量较高，这与文献［9－10］结果一致.文献［11］则利用这一特点来识别锥形涡.

图7给出0°风向角下封闭式曲面屋盖风压系数场POD分解的前3阶特征向量的等值线图.从图7可以看出，第1阶特征向量与屋盖平均风压系数分布较为相似，主要反映平均风压分布，此结论与文献［12］结论一致，其来由可由准定常理论解释，根据准定常理论，随时间变化的风压系数分布可表示为：

式中：u（t），v（t），w（t）分别为在x，y，z3个方向的风速脉动；U为平均风速.

而第2阶和第3阶特征向量则与平均风压系数分布相差较远，反映的是平均风压系数与其位置的偏导关系，其物理解释为来流的气流分离涡的形成所致［12］，反映风压的局部分布特征.

图8为180°风向角下开合式曲面屋盖表面净风压系数场POD分解的前3阶特征向量等值线图.由图8可以看出，由于前3阶模态占总风压系数场能量的比重较大，其表面第1阶特征向量等值线图基本反映了表面平均风压系数分布的整体趋势，第2阶和第3阶特征向量反映局部风压分布.

比较图6，图7和图8可知，3种屋盖的第1阶特征向量均可以较好地反映平均风压系数的分布特征，其高阶分布具有较明显的差别，POD分解性能最优的45°风向角的方形平屋盖的2阶分量可以明显反映其特征湍流锥形涡分量，而开合式曲面屋盖和封闭式曲面屋盖的高阶则反映的是风压系数的局部特征.

图6 封闭式方形平屋盖风压系数场POD分解的前4阶特征向量等值线图Fig.6 First four POD modes of the measured wind pressure field for closed flat roof

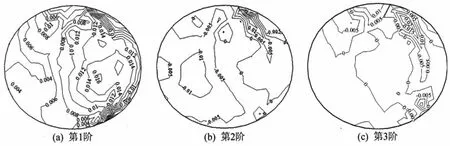
图7 封闭式曲面屋盖风压场前3阶POD特征向量分布（0°风向角）Fig.7 First three POD modes of the measured wind pressure field for closed curved roof（0°）

图8 开合式曲面屋盖前3阶POD特征向量分布（180°风向角、开合屋盖开启）Fig.8 First three POD modes of the measured wind pressure field for retractable roof（180°）

5 平屋盖风压场重建

利用POD分解可对风压场数据进行分解压缩，原有的风压场数据可通过少数阶的特征向量和时间主坐标进行重建.为研究风压场重建效果，选取封闭式方形平屋盖0°风向角下的3个典型测点（6，46和76号测点）来进行分析.其中，6号测点位于气流分离区，平均风压系数和脉动风压系数分别为－0.82和0.22；46号测点位于气流再附区域，平均和脉动风压系数分别为0.06和0.04；76号测点位于尾流区，平均和脉动风压系数分别为－0.2和0.09.

图9给出了0°风向角下封闭方形平屋盖典型测点的POD重建风压系数时程与目标时程的比较，为了便于比较，图9横坐标采用风洞试验时间.从图9可以看出：1）对于相同测点，考虑的模态阶数越多，重建效果越好；2）对于不同测点，采用相同模态阶数进行风压系数重建的精度差异较大，气流分离区处的6号测点精度最优，其次为尾流区的76号测点，再附区的46点效果最差.6号测点重建效果最优，主要原因是因为气流分离区脉动风压系数最大，而POD方法重建脉动风压场具有不平衡性，其重建效果向脉动风压系数大的测压点倾斜.对于76号测点，再附区的正风压是一个局部的突变（见图3（a）），需要高阶模态才能反映其特征，采用低阶模态进行重建则效果不佳.

图10给出了0°风向角下封闭方形平屋盖典型测点（6号，46号和76号测点）的POD重建风压谱与目标谱的比较.从图10可以看出：1）对于相同测点，考虑的模态阶数越多，风压谱重建效果越好；2）对于不同测点，气流分离区测点6重建效果最佳，46号测点次之，76号测点效果最差.

图9 封闭方形平屋盖典型测点POD重建效果比较（0°风向角）Fig.9 Comparison of the reconstructed wind pressure coefficients time history with measured results（0°）

图10 平屋盖典型测点POD重建功率谱比较Fig.10 Comparison of the reconstructed wind pressure coefficients spectra density with measured results

6 结 论

基于封闭方形平屋盖、封闭曲面屋盖和开合式曲面屋盖刚性模型同步测压风洞试验，研究了POD方法对于上述3种类型屋盖的适用性，并对封闭方形平屋盖的风压场数据进行重建，结果表明：

1）开合屋盖屋顶开启时其平均风压系数要明显小于封闭式平屋盖和曲面屋盖，但脉动风压有所增加；

2）由3类屋盖POD分解的特征值可以看出，斜风向封闭平屋盖的POD分解性能最优，其次为可开合式曲面屋盖，封闭式曲面屋盖最差；

3）由3类屋盖POD分解的特征向量分布可以看出，3种屋盖的第1阶POD特征向量均反映平均风压系数分布，对于45°风向角方形平屋盖的第2阶POD模态可以较好地反映其特征湍流锥形涡分量，而其他类型屋盖的高阶特征向量反映的则为风压场的局部分布；

4）由大跨平屋盖风压场的重建时程和重建功率谱比较可以得到POD重建具有较明显的不平衡性能，对于相同测点，模态数越多，其重建效果越好；而对于不同测点，测点脉动风压系数越大，其风压重建效果越好，而采用少数阶模态重建高脉动风压系数测点亦有较好的效果.

［1］ BIENKIEWICZ B，TAMURA Y.Proper orthogonal decomposition and reconstruction of multi-channel roof pressure［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，54：369－381.

［2］ HO T C E，DAVENPORT A G.Characteristic pressure distribution shapes and load repetitions for the wind loading of low building roof panels［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，57（2／3）：261－279.

［3］ JEONG S H，BIENKIEWICZ B.Application of autoregressive modeling in proper orthogonal decomposition of building wind pressure［J］.Journal of Wind Engineering and Industrial Aer-odynamics，1997，69：685－695.

［4］ JEONG S H，BIENKIEWICZ B.Proper orthogonal decomposition of building wind pressure specified at non-uniformly distributed pressure taps［J］.Journal of Wind Engineering and Industrial Aerodynamics，2000，87（1）：1－14.

［5］ 李方慧，倪振华，谢壮宁.POD方法在重建双坡屋盖风压场中的应用［J］.工程力学，2005，22：177－182.

LI Fang-hui，NI Zhen-hua，XIE Zhuang-ning.Application of POD to reconstruction of wind pressure fields of pitched roof［J］.Engineering Mechanics，2005，22：177－182.（In Chinese）

［6］ 李元齐，沈祖炎.本征正交分解法在曲面模型风场重构中的应用［J］.同济大学学报，2006，34（1）：22－26.

LI Yuan-qi，SHEN Zu-yan.Application of proper orthogonal decomposition method to wind field reconstruction of models with curved surfaces［J］.Journal of Tongji University，2006，34（1）：22－26.（In Chinese）

［7］ CHEN Xin-zhong，KAREEM A.Proper orthogonal decomposition-based modeling，analysis，and simulation of dynamic wind load effects on structures［J］.Journal of Engineering Mechanics，2005，131（4）：325－339.

［8］ 李寿科，李寿英，陈政清.开合屋盖体育场风荷载特性试验研究［J］.建筑结构学报，2010，31（10）：17－23.

LI Shou-ke，LI Shou-ying，CHEN Zheng－qing.Experimental investigation on wind loading of a stadium with a retractable roof［J］.Journal of Building Structures，2010，31（10）：17－23.（In Chinese）

［9］ KAWAI H.Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flows［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69：579－588.

［10］GILLIAM X，JAMES P D.Using projection pursuit and proper orthogonal decomposition to identify independent flow mechanisms［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92（1）：53－69.

［11］RUAN Dan，HE Hua，CASTANON D A.Normalized proper orthogonal decomposition for building pressure data compression［J］.Journal of Wind Engineering and Industrial Aerodynamics，2006，94（6）：447－461.

［12］UEMATSU Y，YAMADA M.Wind loads and wind-induced dynamic behavior of a single-layer latticed dome［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，66（3）：227－248.

Proper Orthogonal Decomposition and Reconstruction of Wind Field for Large-span Roofs

LI Shou-ke，LI Shou-ying†，CHEN Zheng－qing，HUANG Tao
（Wind Engineering Research Center，Hunan Univ，Changsha，Hunan 410082，China）

Wind tunnel tests were carried out to measure the wind pressure on the closed flat roof，closed curved roof and retractable roof.The characteristics of mean and fluctuating wind pressure coefficients were particularly studied.The wind pressure fields of the roofs were decomposed in the proper orthogonal decomposition method，and the wind pressure field of flat roof was reconstructed.It has been shown that the performance of POD of oblique wind flat roof behaves best among all the three roofs，retractable roof is second，and closed curved roof is the worst；The overall distribution of mean wind pressure is reflected by the first dominant eigenvectors of POD.The POD reconstruction performance varies a lot among individual taps.The same taps have better performances for more eigenvectors.Different taps have better performances for higher variance taps.

wind tunnels；closed flat roof；closed curved roof；retractable roof；Proper Orthogonal Decomposition（POD）

TU311.3

A

1674-2974（2011）06-0020-07＊

2010-09-09

国家自然科学基金资助项目（50708035）

李寿科（1981－），男，江西萍乡人，湖南大学博士研究生

†通讯联系人，E-mail：shyli＠hnu.cn