首次积分法下非线性偏微分方程的精确行波解*
刘开宇,党军杰
(湖南大学数学与计量经济学院,湖南长沙 410082)
首次积分法下非线性偏微分方程的精确行波解*
刘开宇†,党军杰
(湖南大学数学与计量经济学院,湖南长沙 410082)
针对一类非线性偏微分方程,提出行波解的存在性问题.通过引入波变量,利用基于交换代数环论的首次积分方法,直接得到2种非线性演化方程模型的精确行波解.首次积分法较之传统的技巧更方便、更快捷.因此首次积分法在解决某些非线性方程的复杂孤波解时是一种有效并且有着巨大潜力的方法.
非线性微分方程;行波解;首次积分法
关于非线性偏微分方程行波解的探讨在研究非线性物理现象中起着非常重要作用、非线性波动现象出现在各种科学和工程领域,如流体力学、等离子体物理、光学纤维、生物、固体物理、化学动力学、化学物理和地球化学等.非线性波的色散、耗散、扩散、反应和对流现象在非线性波动方程中是非常重要的,新的精确行波解可以帮助人们发现新的现象.为此,在过去的几十年里人们做了大量工作,提出了许多有效的方法,如齐次平衡法[1]、双曲正切值扩展方法[2-3]、雅可比椭圆函数展开法[4-7]、sine-cosine法[8-9]、tanh函数法[10-11]等等.运用上述方法求解非线性演化方程的一个共同特点,就是要利用Maple或Mathematica软件作繁琐计算.近年来,出现了一个非常有效的新方法——首次积分法.该方法是基于交换代数环的理论[12],我们可用它研究多种非线性演化方程的行波解[13-14].运用首次积分可以方便、快捷地求出某些非线性演化方程的精确孤波解,与传统方法相比它具有许多优点,它主要避免了大量复杂和繁琐的计算,提供了精确、明确的孤波解.
1 首次积分法
Raslan[15]对运用首次积分法的步骤作了如下总结.
步骤1 考虑如下一般非线性偏微分方程(PDE):


引入波变量ξ=x-ct.于是方程(1)可表示为非线性常微分方程(ODE):式中.如果式(2)中含有阶数高于2的导数,我们假定通过积分后可使所含的最高导数阶数是2(见方程(4)).
步骤2 在ODE式(2)中引入新的独立变量

步骤3 由常微分方程的定性理论,如果能够找到相同条件下式(3)的积分,则可以直接求出式(3)的解.然而,一般来说,这的确是很困难的.因为对于一个给定的平面自治系统,我们既没有一个系统的理论,也没有一个逻辑方法可用来获得它的首次积分.我们将运用除法定理获得式(3)的首次积分,通过求解这个方程从而得到方程(1)的精确解.下面我们给出除法定理.
除法定理 假设P(w,z),Q(w,z)是定义在复数域C(w,z)上的2个多项式,且P(w,z)是C(w,z)上的既约多项式.若Q(w,z)在P(w,z)的所有零点均为零,则存在C(w,z)上的多项式G(w,z)使得:
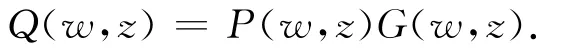
除法定理易由文献[12]中的交换代数环定理得到.
2 Fornberg-Whitham方程
Fornberg-Whitham方程为:
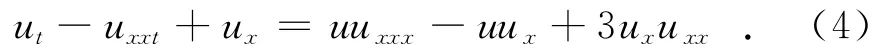
方程(4)是在研究波裂的定性行为时由Fornberg-Whitham提出的[16-17],它是一个非线性色散波动方程,由于式(4)是一个派生方程,关于它的研究并不多见.在文献[17]中Fornberg和Whitham得到了一个如下形式的尖峰波解:

其中A为任意常数.
下面我们用首次积分法进行研究.若方程(4)有如下形式的行波解:

利用式(3),方程(7)可改写为二维自治系统:

式中:ai(X),i=0,1,…,m为关于X的多项式且am(X)≠0.则方程(10)称为式(9)的首次积分.由除法定理,存在复数域C[X,Y]上的多项式g(X)+h(X)Y,使得
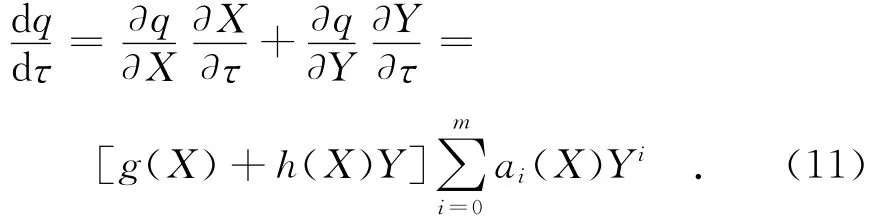
为简便起见,对方程(10)我们取m=1.通过比较方程(11)两边Yi(i=0,1)的系数,可得
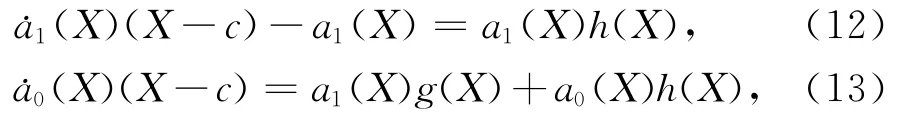

3 变形Boussinesq方程

作为水波模型,u表示波速,H为总深度,方程中右下标记表示偏导数.假设方程(16)有下面形式的行波解:

我们考虑如下变形Boussinesq方程[18]:

式中c0为积分常数.
通过与文献[18]中所得结果比较,我们所得到的解的表达式更为简单.
4 结 论
本文利用首次积分建立2种非线性演化方程的精确行波解.许多为人们熟知的非线性波动方程均可用这种方法处理,由此可见这一方法是非常行之有效的.相比于其他传统方法,它的优势在于避免了大量复杂和繁琐的计算,提供精确和简单行波解的表达式,同时能给出多个显式解.
[1] WANG M L.Exact solutions for acompound Kd V-Burgers equation[J].Phys Lett A,1996,213:279-287.
[2] YANG L,LIU J B,YANG K Q.Exact solutions of nonlinear PDE,nonlinear transformations and reduction of nonlinear PDE to a quadrature[J].Phys Lett A,2001,278:267-270.
[3] PARKES E J,DUFFY B R.Travelling solitary wave solutions to a compound Kd V-Burgers equation[J].Phys Lett A,1997,229:217-220.
[4] FAN E,ZHANG J.Applications of the jacobi elliptic function method to special-type nonlinear equations[J].Phys Lett A,2002,305:383-392.
[5] YOMBA E.The extended fan’s sub-equation method and its applications to Kd V-Mkd V,BKK and variant Boussinesq equations[J].Phys Lett A,2005,336:463-476.
[6] ZHOU Y B,WANG M L,WANG Y M.Periodic wave solutions to a coupled Kd V equations with variable coefficients[J].Phys Lett A,2003,308:31-36.
[7] ZHANG S.New exact solutions of the Kd V-Burgers-Kuramoto equation[J].Phys Lett A,2006,358:414-420.
[8] WAZWAZ A M.A sine-cosine method for handling nonlinear wave equations[J].Math Comput Model,2004,40:499-508.
[9] WAZWAZ A M.Analytic study on nonlinear variant of the RLW and the PHI-four equations[J].Commun Nonlinear Sci Numer Simul,2007,12:314-327.
[10]YAN Z Y.New explicit travelling wave solutions for two new integrable coupled nonlinear evolution equations[J].Phys Lett A,2001,292:100-106.
[11]WAZWAZ A M.Travelling wave solutions of generalized forms of Burgers,Burgers-Kd V and Burgers-Huxley equations[J].Appl Math Comput,2005,169:639-656.
[12]BOURBAKI N.Commutative algebra[M].Paris:Addison-Wesley Publishing,1972:20-45.
[13]FENG Z.Exact solutions in terms of elliptic functions for the Burgers-Kd V equation[J].Wave Motion,2003,38:109-115.
[14]FENG Z.Travelling wave behavior for a generalized fisher equation[J].Chaos Soliton Fract,2008,38:481-488.
[15]RASLAN K R.The first integral method for solving some important nonlinear partial differential equations[J].Nonlinear Dynamics,2008,53(4):281-287.
[16]WHITHAM G B.Variational methods and applications to water wave[J].Proc R Soc Lond Ser A,1967,299:6-25.
[17]FORNBERG B,WHITHAM G B.A numerical and theoretical study of certain nonlinear wave phenomena[J].Philos Trans R Soc Lond Ser A,1978,289:373-404.
[18]WANG M L.Solitary wave solutions for variant Boussinesq equations[J].Physics Letters A,1995,199:169-172.
Exact Travelling Wave Solutions of Nonlinear Partial Differential Equations by Using the First Integral Method
LIU Kai-yu†,DANG Jun-jie
(College of Mathematics and Econometrics,Hunan Univ,Changsha,Hunan 410082,China)
Considering the many models of nonlinear partial differential equations existing in physics and other fields,the existence of exact travelling wave solutions of equations was proposed.By introducing a wave variable and using the first integral method based on the ring theory of commutative algebra,we have obtained the exact travelling solitary wave solutions for two nonlinear evolution equations.It has many advantages over other traditional techniques,it is direct and concise.It also shows that the first integral method is an effective method with great potentials when finding complex solitary wave solutions of the nonlinear equations.
nonlinear differential equations;travelling wave solutions;first integral method
O175.12
A
1674-2974(2011)06-0089-04*
2010-06-15
国家自然科学基金资助项目(10601016);教育部留学回国人员科研启动基金资助项目
刘开宇(1964-),女,湖南长沙人,湖南大学副教授,博士
†通讯联系人,E-mail:Liukyhnu@yahoo.com.cn

