一种新型的变领域搜索算法

于继江

(菏泽学院 计算机与信息工程系，山东 菏泽 274015)

0 引言

变邻域搜索算法（VNS, Variable Neighborhood Search）是一种求解优化问题的启发式算法，是有 Hansen 和Mladenovic´首次提出。它的基本思想在搜索过程中系统地改变邻域结构集来拓展搜索范围，获得局部最优解，再基于此局部最优解重新系统地改变邻域结构集拓展搜索范围找到另一个局部最优解的过程。由于VNS在简易性、时效性、人性化和创新性等方面表现突出，若干改进算法已应用于NP难问题的求解中[1-4]。

VNS提出后被应用于很多组合优化问题的求解，许多应用实例也表明了VNS对解决组合优化问题的优越性能[5-7]。对于组合优化问题，一个邻域内的可行解是有限的，因此在局部搜索过程中，是可以计算出邻域内的所有可行解的目标函数值，进而找到邻域内的最优解，即局部最优解。区别于组合优化问题，连续优化问题中的可行解空间是连续的，因此无法找到邻域内所有可行解，也就无法找到局部最优解。

针对上述问题，提出了一种结合序列二次规划法(SQP,Sequential Quadratic Programming)的变邻域搜索方法，并将其应用到无约束连续优化问题中。

1 结合SQP的变邻域搜索算法

SQP是当前公认的处理中、小规模非线性规划问题最优秀的算法之一，它具有良好的局部收敛性和较强的超线性收敛速度。它能快速精确地获取当前点附近的局部极小点。为了较好处理VNS中的局部搜索过程，更快速、更精确得到局部最优解，将SQP结合到VNS中，即应用SQP求解局部搜索过程中的局部最优解。这样既保持了SQP在求解局部最优解上的优势，又突出了VNS全局收敛性的特点。

对于一个问题 P，设初始解为 x，邻域结构 Nk(x),k=1,2,…,kmax，设定参数的初始值，kmax,tmax,kstep，其中kmax为最大邻域，tmax为最大计算时间，kstep是每次迭代的邻域步数。

结合SQP的VNS算法流程如下：

①令k=1；②随机选取x的 p邻域中的一点x′（x′ ∈Np(x)）；③以x′为初始解，运行SQP算法，获得局部最优解x′；④若 f(x′′)＜f(x)，令 x=x′′，转到步骤①，反之，令 k=k+kstep，转到步骤②；⑤若终止规则满足，则终止计算。

在VNS的应用中，为了加快算法的运行速度、提高算法的搜索精度，可以采用以下策略改进算法。

（1）初始点策略

在VNS中初始点的选取，对最后得到的最优解和运算时间、迭代步数有直接的影响，若初始点选取的好，能够尽可能的靠近全局最优解，得到全局最优解所需要的时间以及迭代步数就会减少。在初始点选取中，可以采用多点选择，取目标函数值最小的一个点作为初始值。

（2）多样性策略

在VNS中一般包含3个部分：随机扰动、局部搜索、邻域变换。当通过局部搜索过程，找到一个局部最优解时，利用随机扰动的方法，在距离局部最优解一定距离的地方，选取一个可行解作为新的局部搜索的起始点。这样就能够从局部最优解的“山谷”中脱离出来，从而找到全局最优点。

一般VNS中，每次的随机扰动都只是选择k邻域中的一点。当邻域比较大时，邻域内的可行解数量就会比较多，由于扰动的随机性，只随机选取一点，有可能就会漏掉全局最优解。因此，可以采用多样性（Diversification）策略，选取邻域内的多个点作为起始点，对每个点进行局部搜索，选取其中最优的局部最优解与现有最优解比较。这样可以尽可能的搜索整个区域，以达到寻找全局最优解的目的。

对于一个问题 P，设初始解为x，邻域结构Nk(x),k=1,2,…,kmax，设定参数的初始值，kmax,tmax,kstep，其中kmax为最大邻域，tmax为最大计算时间，kstep是每次迭代的邻域步数。

改进的VNS算法流程如下：

以上算法中多样性部分可以用并行化处理。

2 数值实验

实验所用的计算机配置Core2 Duo CPU，主频2.17 GHz，2 GB内存，操作系统为 windows7，使用的编程软件是MATLAB2009.优化算法的比较通常是基于一些标准函数的典型问题展开的通过5个标准函数(见表1示)测试算法的性能。这些函数具有多峰、非凸等特点,经常被国外学者用于对优化问题的测试。

表1 5个标准的测试函数

首先比较所提出的VNS算法与纯SQP算法的求解效果。对于VNS算法，首先在可行域内随机选取了20个点，选择其中目标函数值最小的作为初始解，邻域半径差为 0.1，最大迭代次数 kmax=20。SQP算法采用MATLAB优化工具箱中的fmincon函数。为了使结果具有可比性，两种算法都从相同的初始解开始，对每个函数（前两个函数取n=2）做了 5次实验，对比了最优解的情况，得到的结果如表2。

从表2可以看出，VNS算法具有很好的全局收敛性，最优解和目标函数值都能够精确到 1e-8以上，寻优的精确性都远好于单纯的SQP算法。特别对于测试函数Shubert，使用 VNS算法，很容易找到了全部 18个最优解，分别是：(-7.7083,-7.0835),(-7.7083,-0.8003),(-7.7083,5.4829),(-7.0835,-7.7083),(-7.0835,-1.4251),(-7.0835,4.8581),(-1.4251,-7.0835),(-1.4251,-0.8003),(-1.4251,5.4829),(-0.8003,-1.4251),(-0.8003,4.8581),(-0.8003,-7.7083),(4.8581,-7.0835),(4.8581,-0.8003),(4.8581,5.4829),(5.4829,-7.7083),(5.4829,4.8581),(5.4829,-1.4251)。由此可以看出，VNS算法的有效性。

然后，比较所提出的VNS算法与其他算法的求解效果。选用了粒子群算法（PSO，Particle Swarm Optimization）[8-9]、遗传算法（GA,Genetic Algorithms）[10]与 VNS算法进行比较。VNS算法延用上一部分的参数设置；PSO算法取了20个粒子，进行了200次的迭代；GA算法选取种群规模为100，最大遗传代数为200，交叉采用线性重组，交叉概率为0.9，高斯变异，其它参数使用缺省值。利用上述3种算法，对第1节中的5个测试函数分别进行了50次的实验，其中对前两个函数，n分别取了2、5、10。首先对比了50次实验的平均最优值、最小最优值和以及到达全局最优值的比率(简称为比率)，所有数据精确到万分位，具体结果如表3示。

由表3可以看出，VNS在全局收敛性上要好过PSO和GA，对5个函数来说，VNS都能够取到全局最优解，而且取到全局最优解的比率也远远高于其他两种算法，特别是当可行解空间维数较小时，几乎每次都能够到达全局最优值。随着可行解空间维数的增大，算法的收敛性会有所下降，但是依然要好过其他两种算法。只是再算法的稳定性上稍差，最优解的平均值要比其他两种算法高，不过在可以接受的范围之内。

对比了50次实验中所用的平均时间和达到最小最优值的最小时间，具体结果如表4。

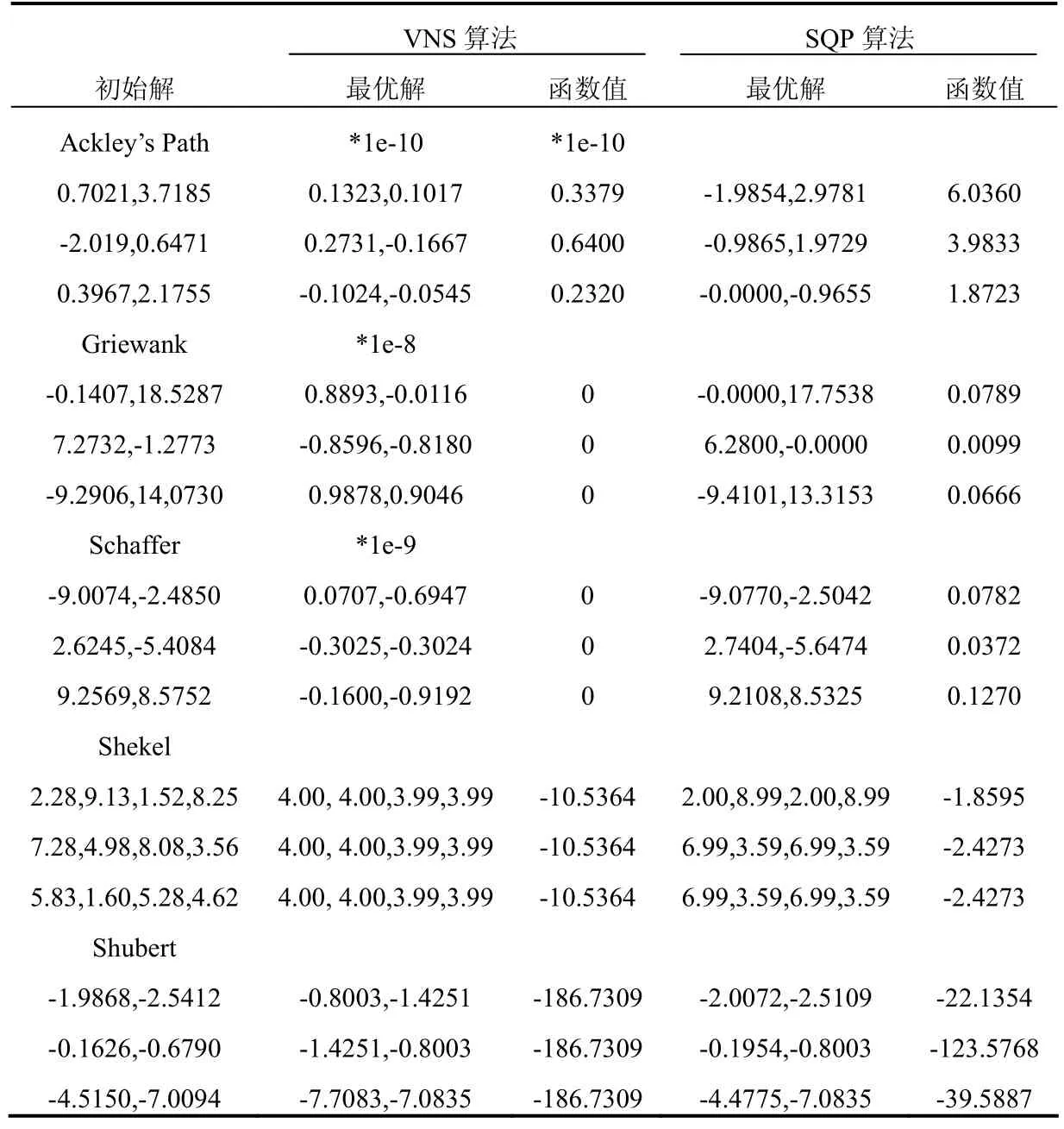
表2 VNS算法与纯SQP算法的求解效果比较

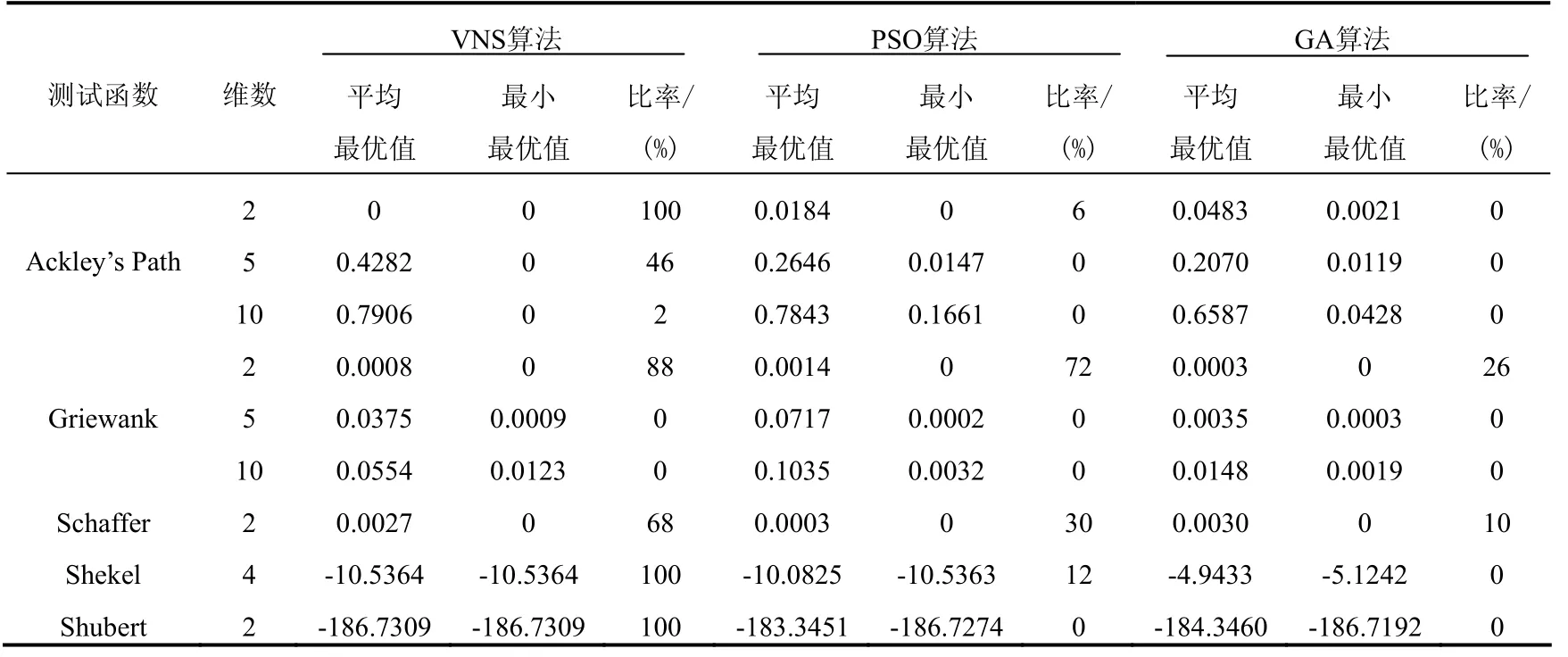
表3 算法求解的最优值比较

表4 算法耗时比较

由表4可以看出，VNS所用的时间要比PSO和GA多，特别是当空间维数比较大时。这是因为在VNS过程中，需要大量运算求目标函数值，当空间维数比较大时，求解目标函数值需要的时间就比较多。但是，相对于VNS算法的收敛性，特别是在空间维数小时，所用时间依然在可承受的范围内。

3 结语

提出了一种结合SQP的VNS算法，用来解决大量非线性、不可微和多峰值复杂问题的优化。该算法能够保持SQP局部寻优能力强的优点和VNS的全局收敛性。通过实验证明，该算法是一种有效的全局优化方法，相比于其他启发法具有更强的寻优能力和更高的搜索精度。

[1] HANSEN P, MLADENOVIC´ N.Variable Neighborhood Search:Principles and Applications[J].European Journal of Operational Research, 2010, 36(03): 449–467.

[2] TOKSARI D, GUNER E.Solving the Unconstrained Optimization Problem by a Variable Neighborhood Search[J].Journal of Mathematical Analysis and Applications,2009, 32(08):1178-1187.

[3] MLADENOVIC´ N, DRAZIC M.General Variable Neighborhood Search for the Continuous Optimization[J].European Journal of Operational Research, 2009, 19(01):753-770.

[4] GARCIA C, PEREZ-BRITO D.Variable Neighborhood Search for the Linear Ordering Problem[J].Computers & Operations Research,2010, 33(03): 3549-3565.

[5] 王明兴.连续禁忌搜索算法改进及应用研究[D].杭州：浙江大学，2009.

[6] 杨敬.禁忌搜索与SQP相结合的混合优化算法研究[D].杭州：浙江大学，2009.

[7] 刘忠耀,彭重嘉,伍乃骐.基于禁忌搜索算法的生产调度[J].微计算机信息,2008,24(02):55-57.

[8] 刘小聪,刘洪武.基于粒子群算法的预编码设计[J].通信技术,2010,43(09):37-39.

[9] 池越,赵东明,夏克文,等.基于QPSO算法的信道分配方法[J].通信技术,2009,42(02):204-207.

[10] 肖冬荣,杨磊.基于遗传算法的关联规则数据挖掘[J].通信技术,2010,43(01):205-207.