双排刚性桩屏障对平面SH波的隔离性状研究

夏唐代,孙苗苗,陈 晨,陈炜昀

（浙江大学 岩土工程研究所,杭州 310058）

车辆荷载、建筑施工等引起的振动因其干扰人们的日常生活而对周围环境产生了不容忽视的影响,并已成为学者关注的热点问题。采用屏障是隔离环境振动的有效措施。目前采用较多的有2种屏障形式,一种是连续屏障,主要有空沟、填充沟,混凝土墙等形式,对于连续屏障的研究已较为成熟。最早由Barkan[1]和Richart[2]对空沟和钢板桩屏障进行了试验研究;其后Woods[3]进行了一系列的现场原位测试,并首次提出用无量纲振幅比ARC来评价屏障的隔振效果;但是在地下水位较高或者软土地区,连续屏障的施工难度加大因而增加了施工和维护的费用,非连续屏障便成为近年来在软土地区运用广泛的隔振手段之一。

非连续屏障对弹性波的散射研究起步较晚,目前较多采用排桩和排孔等形式。Woods[4]运用全息照相技术原理,对瑞利波波场中圆孔屏障隔振进行了研究;Liao和Sangrey[5]用模型桩屏障做试验得出柔性桩比刚性桩的隔振效果更好的结果;Boroomand和Kaynia[6]用简化的地基模型来检验单排桩的隔振效果;Avilés和 Sánchez-Sesma[7-8]研究了单排实心桩对P波、S波及R波的散射问题;Kattis[9-10]等运用三维频域边界元技术分析了实心桩和方桩的隔振作用;徐平等[11-12]研究了刚性空心管桩屏障对平面P、SH和SV波的隔离效果;Cai[13-14]等分析了饱和多孔弹性介质中单排桩的屏蔽作用;Lu[15-16]等对用排桩隔离移动荷载产生的振动进行了详细的研究。

迄今为止,上述文中所述的计算非连续屏障对平面波的隔离问题都只考虑了单重散射,单重散射假设的不足在于它忽略了散射体也就是桩列作为一个整体相互之间相干相位关系,仅仅在桩间距较大的时候才是正确的;而在实际工程中,通常采用的排桩间距较小,排桩体系作为整体屏障起到作用。并且,多个任意排列,任意半径大小的桩屏障对平面波多重散射问题的精确解尚未见报道。该文引入圆柱体对声波和电磁波的多重散射解[16-17],提出了一种新的考虑多重散射的方法来求解平面SH波入射下任意排列任意直径的刚性桩的散射问题。

1 波函数展开

1.1 问题的基本公式

如图1所示,各向同性的无限均质弹性介质的土体中含有任意排列的任意半径圆柱形刚性桩,假设桩长远大于桩径,则该问题可以简化为二维平面问题。入射平面SH波（偏振方向平行于桩身轴线）应满足Helmholtz方程：

图1 任意布置、任意半径圆柱形桩对SH波的散射计算简图

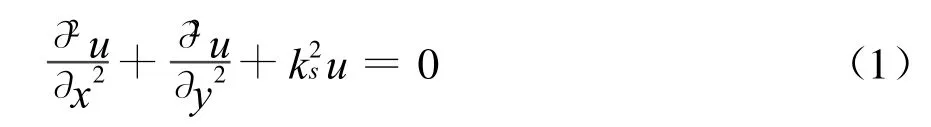
式中ks=ω/c,称为土体中SH波的波数,ω为圆频率,c=G/ρ,其中G和ρ分别为土体的剪切模量和密度。

在第s根桩的坐标系下,满足上述方程的入射SH波可以表示为

式中上角标inc表示入射,这里为了研究和讨论方便,运动量中的时间因子exp（-iωt）（i= -1为虚数单位,t为时间）均被省略。

基于变量分离法,设第s根桩对SH波第m重散射解可表示为

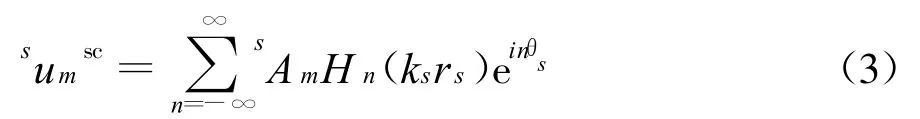
式中上角标sc表示散射,H n（◦）为第一类Hankel函数,n为阶数。s Am为每根桩第m重散射的待定复系数（s Am系数随散射重数m而不同）。

因此可得总共s根桩的总散射波解为

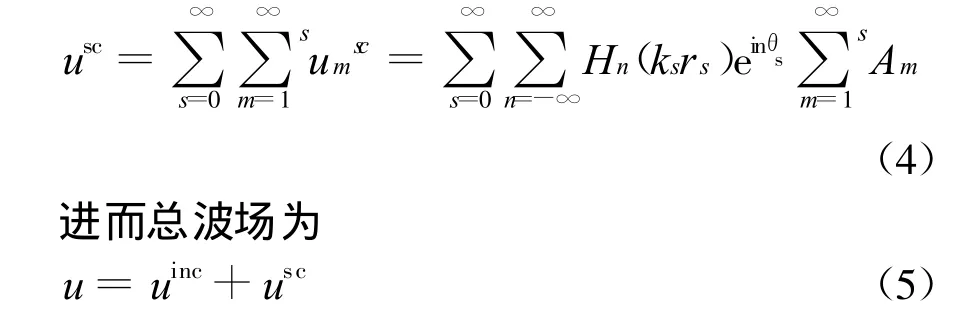
1.2 散射系数的求解

对于任意排列的刚性圆柱桩,计算简图如图1所示。以第s桩为例,假定桩半径为as,选定s=0时的桩中心为参考坐标系原点,每根桩各自坐标轴都平行于参考坐标轴。远场P点可以用与s桩的距离rs和角度θs确定,s′桩相对于参考坐标系的坐标可用（rss′,θss′）确定 。例如P点对于s′桩坐标系的坐标为（rs′,θs′）,s′桩相对 于 0 桩 的坐标为（r0s′、θ0s′）等 。为了求出散射系数s Am,首先考虑m=1的第一重散射的散射系数s A1,因刚性桩埋置得足够深,假设土体与刚性桩界面完全联结,即桩与周围土体界面处满足位移连续条件,则第一重散射的边界条件为：

其中s A=-Jn（ks as）/H n（ksas）,r0s为s=0时远场P点到0桩的距离矢量。

其次考虑第s根桩被其余桩的第一重散射波所激发,产生第二重散射波,同样可以假设第二重散射在桩土界面处也满足边界条件

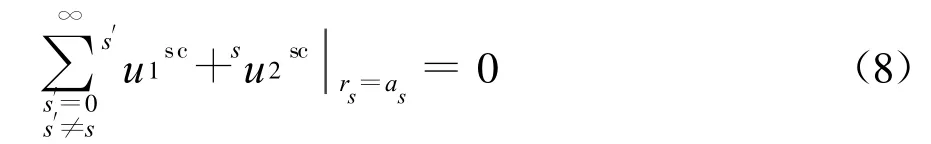
即可求出第二重散射系数s A2：

为了便于相加,需要把s′u1sc化为s点坐标下的函数,根据Graf加法原理,

2 数值计算和分析

2.1 单排桩计算结果分析

假设桩为无限长,入射稳态平面SH波振幅为u0,入射角α,桩排布于同一直线上,桩半径as和桩间距sp均相同,桩数N,为了便于讨论,对位移场的频率进行归一化处理

定义归一化位移幅值为排桩后某处总波场引起的位移幅值与入射波在该处引起的自由场位移幅值的比值。各变量参数取值如下：α=π/2,as=1,sp/as=3.,N=8,ηs=0.4。此算例计算中Bessel函数阶数n截断到8阶已满足精度的要求。

式中λs为土体中SH波长。

图2 单排N根桩屏障计算模型及参考坐标系

图3分别为不同散射重数（m=1～4）屏障后中线上土体无量纲位移幅值随y/as（-20≤y/as≤500）的变化曲线,首先从图3中可以得到,屏障前的区域因入射波与散射波的干涉产生振幅放大现象,而在屏障后,靠近屏障处的隔振效果优于远离屏障处。其次当散射重数取3和4时,屏障后无量纲位移的增量很小,当y/as≥150时的值几乎没有变化,曲线重合,说明该理论计算方法同实际情况相符。

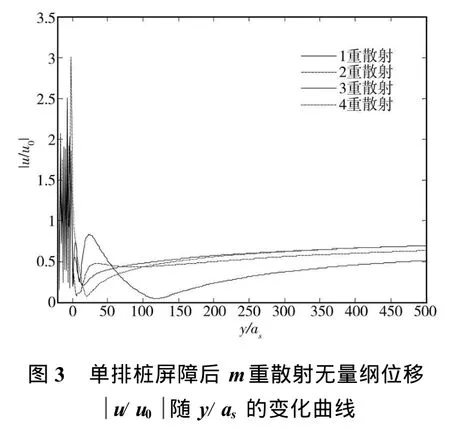
在实际工程中,近场主动隔振的区域在2.5～3.0倍波长内,从图3中可以看到屏障后10≤y/as≤60左右范围内相同位置处的位移幅值随着计算时所取的散射重数增加而减少,多重散射的理论计算结果与以往只考虑单重散射的相比更接近工程实际情况,有一定的工程应用价值。从图3还可以看出,当多重散射的重数取到3重时已经能够满足计算的精度要求,且此结果与文献[7]的结果较为吻合。

图4为位移场不同归一化频率入射波下的单排桩屏障后无量纲位移等值线图,低频波（ηs=0.4）入射时屏障后无量纲位移分布较为平均,靠近屏障区域隔振效果较好,在10≤y/as≤60范围内可以有效隔离80%左右的入射波,因此低频波用单排桩屏障已经能起到较好的屏蔽作用。然而,对于高频波（ηs=1.0）入射时屏障后中心范围内集中出现振幅放大效应,最佳隔离区域向两侧分散,屏蔽作用较为不均匀,单排桩已不能起到较好的屏蔽作用,故可以考虑多排桩屏障进行隔振。

2.2 双排桩计算结果分析

实际工程中对高频入射波较多采用双排桩进行振动污染的隔离,因此双排桩理论计算分析的结果对于工程应用具有重要意义。为了与单排桩屏障进行对比,同样选取屏障参数如下：N=8,α=π/2,as=1,sp/as=3.0,N=8,ηs=1。排桩按两排梅花型布置,计算模型及参考坐标系见图5。

图5 双排N根桩屏障计算模型及参考坐标系

双排桩与单排桩屏障的区别在于双排桩的隔振效果与屏障的厚度即排间距有较大关系。图6考查了排距对隔振效果的影响（排间距0≤h/as≤3.5）。

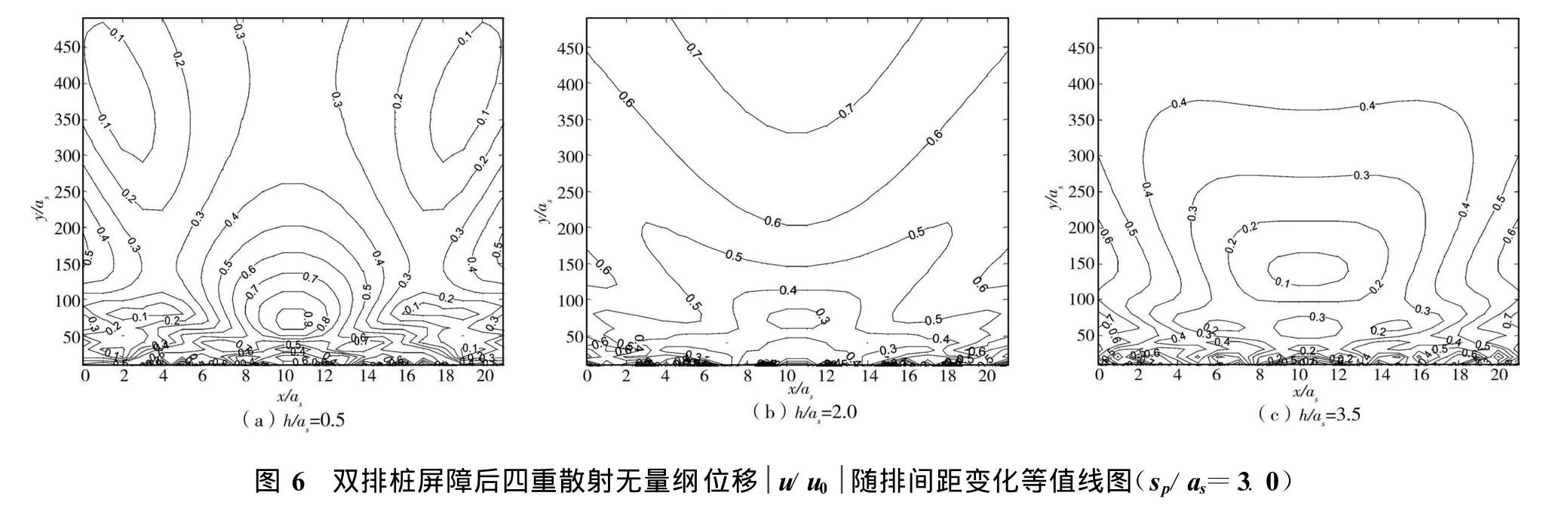
从图6可以看出,屏障后等值线分布规律基本相同,越靠近屏障处屏蔽效果越好。当h/as=0时,双排桩即退化为单排桩,退化解与单排桩屏障的数值计算结果一致,进一步说明本文理论计算方法的正确性。由之前的研究可得,单排桩隔振的屏蔽区域较小,且排桩前中心处有明显的振幅放大效应。随着双排桩排距的增加（0.5≤h/as≤2.0）,屏障后20≤y/as≤100范围内无量纲位移减小,屏障后振幅放大效应趋于平均,说明双排桩逐渐作为一个整体对入射波进行隔离。当排间距h/as=3.5时,屏障后20≤y/as≤200较大范围内都能隔离70%～80%的入射波,隔振效果明显优于单排桩。工程中可以选择排间距h/as=3.5作为双排桩隔振屏障的设计依据。

为了讨论桩间距对双排桩隔振效果的影响,考查了不同桩间距下（2.5≤sp/as≤5.0）屏障后中线上无量纲位移随y/as的变化。图7表明桩间距较小时（2.5≤sp/as≤3.0）,屏障后位移减小不明显,屏障未能起到较好的屏蔽作用;当sp/as=3.0时,屏障后一定区域内（20≤y/as≤200）无量纲位移减小,振幅放大效应明显,能有效隔离约70%的入射波,表明此时双排桩作能为整体取得较好的隔振效果;随着桩间距增加（3.0≤sp/as≤5.0）,屏障后无量纲位移明显增加,振幅放大效应减弱,双排桩不再作为整体屏障起到屏蔽作用,因此在实际工程中为了能形成整体屏障,双排桩间距一般应满足sp/as≤3.0。

3 结 论

对排桩隔离环境振动的问题,提出了一种新的计算任意排列任意直径的刚性桩对平面SH波的散射问题方法—多重散射法。通过对单排,以及双排桩后土体竖向位移振幅的研究,对环境振动的污染隔离提出了有意义的建议。数值分析计算的结果表明：

1）排桩作为隔振体以整体屏障发挥作用,文中提出的考虑多重散射的计算方法优于以往只考虑单重散射而不考虑散射波之间相干相位关系假设的单重散射解。散射重数越多,计算结果与实际情况符合得越好,一般取到四重时已满足工程要求。

2）当入射SH波频率较高时可以考虑多排桩进行隔离,多排桩数值计算结果可以退化至单排桩,表明本文理论计算方法的正确性。

3）多排桩隔离效果与屏障厚度和及整体性有关,屏障厚度即排间距,排间距h/as=3.5左右能取得较佳的隔离效果;同时隔振设计中桩间距应满足sp/as≤3.0,屏障才能作为整体发挥作用。

[1]BARKAN D D.Dynam ics of bases and foundations[M].New York：M c Graw-H ill.1962.

[2]RICHART F E,HALL J R,WOODS R D.V ibrations o f soils and foundations[M].Prentice-H all,Englewood cliffs,NJ.1970.

[3]WOODS R D.Sc reening of surface w aves in soils[J].Journal of Solids M echanics and Foundation.Division,ASCE,1968,94（4）：951-979.

[4]WOODS R D,N E BARNET,R SANGESSER.Holography,a new too l for soil dynam ics[J].Journal of Geotechnical Engineering Division,ASCE,1974,100：1231-1247.

[5]LIAO S,SANGREY D A.Use of piles as isolation barriers[J].Journal o f Geotechnical Engineering Division,ASCE,1978,104（9）：1139-1152.

[6]BOROOMAND B,KAYNIA A M.Vibration isolation by an array of piles [C]//First International Conference on Soil Dynam ics and Earthquake Engineering.Karlsruhe,Germany,1992：683-691.

[7]AV ILÉS J,SÁNCHEZ-SESMA F J.Piles as barriers for elastic w aves[J].Journal of Geotechnical Engineering Division,ASCE,1983,109（9）：1133-1146.

[8]AV ILÉS J,SÁNCHEZ-SESMA F J.Foundation isolation from vibrations using piles as barriers[J].Journal of Engineering Mechanics,1988,114（11）：1854-1870.

[9]KATTIS S E,POLYZOS S,BESKOS D E.Vibration iso lation by a row of piles using a 3-D frequency domain BEM[J].International Journal o f Numerical Methods Engineering,1999,46：713-728.

[10]KATTISS E,POLYZOSS,BESKOS D E.Modelling of pile w ave barriers by effective trenches and their screening effectiveness[J].Soil Dynam ics and Earthquake Engineering,1999,18：1-10.

[11]徐平,夏唐代,吴明.刚性空心管桩屏障对P波和SH波的隔离效果研究[J].工程力学,2008,25（5）：210-217.

XU PING,XIA TANG-DA I,WU GANG.Study on the effect of barrier of a row of rigid hollow pipe piles for the iso lation o f P and SH waves[J].Engineering M echanics,2008,25（5）：210-217.

[12]徐平,夏唐代,周新民.单排空心管桩屏障对平面SV波的隔离效果研究[J].岩土工程学报,2007,29（1）：131-136.

XU PING,XIA TANG-DA I,ZHOU XIN-M IN.Study on effect of barrier of a row o f hollow pipe piles on isolation of incident plane SV w aves[J].Chinese Journal of Geotechnical Engineering,2007,29（1）：131-136.

[13]CA I Y Q,DING G Y,XU C J.Screening of p lane S w aves by an array of rigid piles in poroelastic soil[J].Journalof Zhejiang University,Science A,2008,9（5）：589-599.

[14]CA IY Q,DING G Y,XU C J,et al.Vertical amplitude reduction of Rayleigh w aves by a row of piles in a poroelastic half-space[J].International Journal for Numerical and Analytical Methods in Geomechanics,2009,33（16）：1799-1821.

[15]LU J F,XU B,WANG J H.Numerical analysis of isolation of the vibration due tomoving loads using pile row s[J].Journal o f Sound and Vibration,2009,319（3/4/5）：940-962.

[16]WANG JH,ZHOU X L,LU JF.Dynamic response of pile groups embedded in a poroe lastic medium[J].Soil Dynam ics and Earthquake Engineering,2003,23（3）：235-242.

[17]TWERSKY V.Multip le scattering o f radiation by an arbitrary configuration of parallel cy linders[J].Journal of the Acoustical Society of America,1952,24（1）：42-46.

[18]TWERSKY V.Mu ltip le scattering of radiation by an arbitrary p lanar configuration of parallel cy linders and by tw o paralle l cy linders[J].Journal of A pp lied Physics,1952,23（4）：407-414.

（编辑王秀玲）