水网密集区粘土路基当量回弹模量的预估分析

邱 欣,杨 青,钱劲松

(1.浙江师范大学工学院,浙江金华 321004;2.同济大学交通运输工程学院,上海 201804)

水网密集区粘土路基当量回弹模量的预估分析

邱 欣1,杨 青1,钱劲松2

(1.浙江师范大学工学院,浙江金华 321004;2.同济大学交通运输工程学院,上海 201804)

基于非饱和土基本理论,利用基质吸力及土水特征曲线的最新研究成果,对受地下水位控制的粘土路基的平衡湿度状态进行了预估分析;同时采用室内重复动三轴试验方法,建立了非饱和粘性路基土动回弹模量的双线性本构经验预估模型。将上述研究成果相结合,创建了综合考虑路基湿度和应力状态的路基当量回弹模量的预估方法,并结合实体工程建立了以地下水位、路基填筑高度为核心的路基当量回弹模量预估方程。通过与试验路上传统测试方法测试结果的对比分析,表明该评价方法具有准确、可靠特点。研究成果从平衡湿度和应力状态耦合控制的角度,对水网密集区粘土路基当量回弹模量的确定提供了新的视角和途径。

粘土路基;平衡湿度;回弹模量;预估方程

路基是路面的支撑结构物,其性状对于上承路面结构的力学响应和使用性能具有显著影响。在基于力学-经验法的沥青路面结构性能评价分析中,一般采用路基当量回弹模量()来表征路基结构的力学特性,因此的科学评定是完善路面结构承载能力评价分析的一项重要内容[1]。目前,中国相关测试规范中规定采用室内试验法(小承载板法和强度仪法)或现场实测法(承载板法和贝克曼梁法)对路基的进行评价分析,但室内试验中试件无侧限受压,受力状况与现场路基土的实际应力状态不一致,且测试方法与取值标准均缺乏合理性;而现场实测法费时、费力、操作烦琐,变异性大,且测试结果仅适于静态模量标定。近年来广大学者从不同角度对路基结构的ER评定进行了广泛的研究,一方面通过室内外试验建立了基于路基土纯物性指标或力学指标的预估模型[2-3];另一方面则通过落锤式弯沉仪(FWD)检测技术提出了各种反演的方法[4]。但上述分析思想,没有充分考虑路基内平衡湿度状态及应力依赖性对于路基的综合影响,进而导致评价分析结果存在局限性,而这对于水网密集区高地下水位的粘土路基而言问题更显突出。基于此,该文在不改变现有路面结构设计及评价理论体系的条件下,拟将非饱和土湿度预估方法与路基土动回弹模量预估模型的研究成果相结合,采用路表弯沉等效原理,创建了综合考虑路基湿度和应力状态的路基当量回弹模量的预估分析方法,同时结合实体工程建立了以地下水位、路基填筑高度为核心的路基当量回弹模量的预估方程,研究成果对水网密集区粘土路基当量回弹模量的确定具有现实的理论意义和工程实践价值。

1 路基平衡湿度状态预估

1.1 预估模型

路基一般属于经过开挖、重塑和再压实的非饱和土。基质吸力是表达非饱和土工程性质的一项重要参数[5]。当地下水位较高,毛细水上升控制范围较大,粘土路基的湿度往往受地下水位控制,并在基质吸力、重力和填土荷载的共同作用下达到平衡湿度状态[6]。此时可采用描述基质吸力与含水量之间热力学关系的土水特性曲线(Soil Water Characteristic Curve,SWCC)对路基平衡湿度状态进行预估。分析步骤如下：首先,确定路基内某点距地下水位的距离h;其次,预估该点基质吸力,见式1;最后,标定SWCC模型参数,预估路基内某点的体积含水量(θw),并转化为质量含水量。通过对常见SWCC预估模型(Van Genuchten模型、Hillel模型以及Fredlund&Xing模型)适用性的系统论证[8-9],拟采用Fredlund&Xing模型对受地下水位控制的粘土路基平衡湿度进行预估,见式2。

式中,为基质吸力;h为计算点距地下水位的相对距离;为水重度。式中：θw为体积含水量;hr为与剩余含水量对应的基质吸力;θs为饱和体积含水量;α,b,c为模型参数。

1.2 模型参数标定

以沪宁高速(上海段)粘性路基土为例,通过室内物性参数指标的相关测试,结合 Claudia E. Zapata提出的 Fred lund&Xing模型参数标定方法[10],见式(3),对模型参数进行了标定。分析结果见表1。

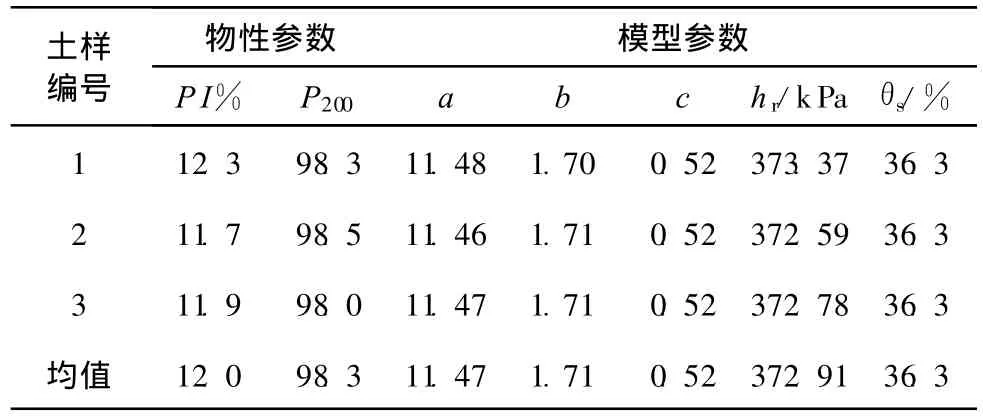
表1 Fredlund&Xing模型参数标定

式中,wPI为加权塑性指数;P200为通过0.074 mm筛的土粒含量;PI为塑性指数。

1.3 平衡湿度预估值可靠性验证

基于Fred lund&Xing土水特征曲线模型,路基内部平衡湿度状态预估结果,如图1所示。为了验证预估结果的正确性,研究中在沪宁高速(上海段)某一评价路段行车道下部利用螺旋钻和环刀进行了场地取土,取土点位粘土路基填高为3 m,地下水位距路表为0.6 m,深度方向取土间隔20 cm,总计14个测点,每个测点3个平行试件,通过室内含水量及击实曲线测试后,并利用式(4)进行了体积含水量与质量含水量的转换,分析得到的路基内部各点实测湿度值与预估湿度值之间的相关关系,如图2所示。由此可知,同一深度测点路基土湿度实测结果与预估值基本相当,比值在0.98～1.03之间,均值为1.01,且彼此之间具有显著的相关性。实际应用中可以通过将基于Fredlund&Xing模型预估出的路基土湿度,利用两者之间的线性相关关系转化为路基土的实际湿度状态。

图1 路基平衡湿度预估结果

图2 路基湿度实测与预估结果对比

2 路基土MR预估模型建立

2.1 路基土常有预估模型分析

路基土动回弹模量(MR)这一概念最初由Seed等人提出,定义为瞬时动态脉冲荷载下动态偏应力与回弹或可恢复应变的比值[11]。概括起来当前预估路基土动回弹模量的模式形式主要包括2类：基于应力状态的本构模型和基于经验关系的回归模型。通过总结归纳可知：基于纯应力状态的本构模型,无法考虑路基内不同点位上湿度状态对回弹模量取值的影响;基于土组纯物性指标的经验回归模型无法体现应力状态对动回弹模量取值的影响。为了综合考虑湿度和应力状态对路基土动回弹模量的影响,分析中通过对粘性路基土实施重复动三轴测试,以建立相应的本构经验预估模型。

2.2 试验方案

三轴重复加载试验是测试路基土动回弹模量的首选方法,在国际上被广泛接纳和应用。参照美国AASHTO路基土与未处治粒料回弹模量试验规程(T292-91)[12],制定了三轴重复加载测试方法。试验仪器为澳大利亚产通用测试仪UTM-100,围压为气压加载。测试试件尺寸为Ø10×20 cm,采用万能液压试验机静压压实成型。试件目标含水量由路基实测湿度状态的取值范围控制,应力状态的影响在应力加载序列中体现,试验中加载序列参照AASHTOT292-91[12]、NCHRP1-28A[3]等试验方法,并根据我国实际路面结构的受力特点而确定[13],见表2。荷载测试波形采用Haversine波;荷载频率为1 H z;加载时间为0.2 s,间歇时间为0.8 s。每一加载级位组合的加载循环次数一般取100,待应变水平稳定后取最后5次的数据计算动回弹模量值。

2.3 测试误差控制

试验中,土样在不同含水量状态下各制备3个平行试件。每个试件的高度和含水量与平行试件均值误差不超过1%。试件加载预压1 000次时,如果垂直永久应变达到5%,预压停止。每个平行试件回弹模量值与平均值之间误差不超过5%。

2.4 MR测试结果及预估模型建立

基于上述动三轴测试方案和相关技术要求,对粘性路基土的进行了测试,测试结果见表2。从测试结果可知：在相同偏应力条件下随围压的增大而增加;在相同围压条件下MR随偏应力的增大而减小,其变化程度远远大于围压的影响,表现了应力软化的特性;不同应力状态下随含水量的增加而显著下降。事实上,对于具有较多塑性的粘性土,其强度主要来源于粘结力,摩阻作用较小,故MR通常由偏应力起主导作用,并随偏应力的增加而下降。分析中充分地考虑粘性土的上述力学行为,以Thompson提出的双线性本构模型为基础对粘性路基土的MR进行了数据拟合分析[14],预估分析模型如式(5)所示。

式中,σd为动偏应力;k1、k2、k3及k4为模型参数。

结合试验测试数据,对模型中及进行了回归分析。数据分析表明,参数和随含水量的变化相对稳定,可取定值(k2=42.75 kPa,=1 110=178)。随含水量的变化相对较大,其与含水量的对应关系,见表3,两者之间的相关性方程,见式(6)。回归方程的显著性F检验结果,见表4。由此可见,在显著性水平为0.01的条件下,F观测统计值＞F0.01(1,4),回归方程高度显著。

表2 MR测试结果

表3 参数k1与含水量的对应关系

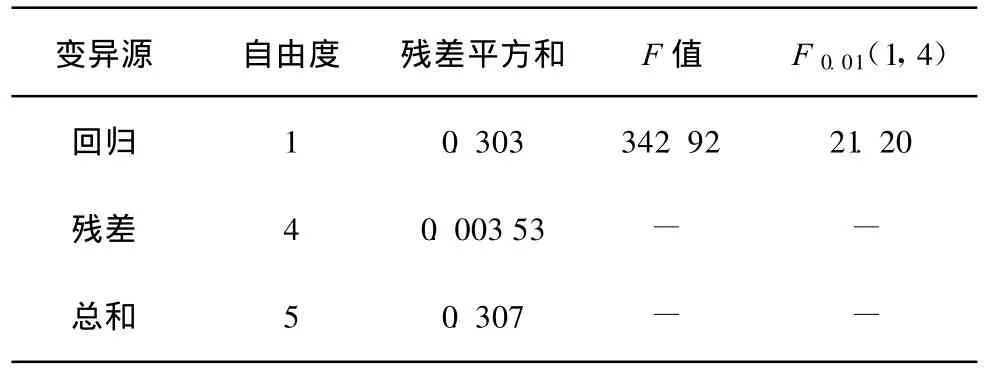
表4 回归方程显著性检验

图3给出了上述预估模型的可靠性分析结果。由此可见,预估值与实测值之间具有较高的相关性,进而表明该文建立的综合考虑湿度及应力状态的粘性路基土双线性本构经验预估模型合理可靠。上述研究成果为基于耦合路基平衡湿度及其粘性路基土的思想,求取水网密集区粘性路基的提供了有利的技术支撑。

3 路基当量回弹模量预估分析方法

3.1 分析实施流程

就水网密集区而言,地下水位是影响非饱和粘土路基内某点湿度状态的关键因素,并与该点所处的应力状态一起,决定了其动回弹模量取值。在不改变当前路面结构设计理论体系的条件下,同时又兼顾应力及平衡湿度对粘土路基力学行为的影响,结合上述研究成果,文章提出采用一种变通的方法进行粘性路基当量回弹模量的预估,如下述：

1)根据地质勘探资料确定地下水位,并将地下水位以上的路基划分为若干亚层,并预估各亚层中部位置的平均基质吸力(hs)。

2)由表征基质吸力与含水量之间相关关系的土水分特征曲线,预估各亚层中部位置湿度值,并根据预估值与实测值之间相关关系,转化为实测值。

3)在不同含水量及应力控制条件下进行路基土室内动三轴测试,建立粘性路基土MR双线性本构经验预估模型,并标定模型参数。

4)基于多层弹性理论体系模型,根据各亚层湿度状态,确定各层MR初使回弹模量值,施加测试荷载求取各亚层中间高度点的偏应力值(σd),结合动回弹模量预估模型及参数标定结果,求取一组新的模量值,并计算出新的一组偏应力值,重复这个过程直至相邻两次迭代的模量差小于某个规定的精度为止(≤1%),最终输出各亚层动回弹模量收敛值,并以此计算路表最大基准弯沉值(l0)。

5)按照路表弯沉等效的原则,将路基看作为弹性半空间体,施加相同测试荷载,反复调整路基ER值,直至路表理论计算弯沉(ls)与路表基准弯沉(l0)之间的差异满足预先给定的收敛精度要求为止(≤0.5μm),并最终确定理论计算值。

图3 MR预测值与实测值之间的相关性

3.2 基本假定

基于上述分析流程,进行路基当量回弹模量预估分析时,作出如下基本假定：

1)考虑结构层自重作用,存在初始应力场,但没有初始变形。

2)计算荷载为静态均布荷载,加载面直径30 cm,荷载集度为0.7 MPa。

3)由于外荷载在路基内某点所产生的附加主应力σ2与σ3可能不等,计算中采用与的平均值作为σ3,同时兼顾上部结构层自重应力在内,采用式(7)计算路基内某点的偏应力(σd)[15]。

式中,σ1、σ2、σ3分别外荷载在路基内某点所产生的附加主应力,kPa;γ为路基土重度,kN/m3;Z为路基内计算点距路表的距离,m为静力土压力系数,分析时取0.8。需要指出的是式(7)在理论上并不正确,因为外荷载产生的主应力不一定和土体自重产生的土压应力方向相同,但由于路基内计算模量的点位选在了加载对称轴上,则保证了上述公式的正确性。

3.3 实体工程E R预估方程

由于实体工程中地下水位随季节常年发生变化,同时由于路线设计标高的差异,既有道路结构不同路段的路基填高也不近相同。为了充分体现路基填高(H)和地下水位距路表距离(h)对的影响,以沪宁高速(上海段)典型半刚性基层沥青路面为例,基于上述分析流程,计算了不同工况组合条件下的值。上承路面结构材料取值及计算结果,分别如表5及图4所示。

表5 实体工程上承路面结构材料参数

图4 不同h和H组合条件下E R计算值

图5 E R预估值与理论计算值的对比分析

基于计算结果,通过多元非线性回归技术,建立了综合考虑h和H的双因素粘性路基的预估方程。分析时首先探讨了不同路基填高H条件下,与h之间的相关关系,回归方程如式(8)所示,表6给出了回归系数a、b与H的对应关系,由此可见,不同H条件下,与h之间的回归方程相关性较高,且回归方程高度显著;其次结合回归系数a、b与H的对应关系,建立了彼此之间的相关性方程,如式(9)、式(10)所示;最后结合式(8)、(9)和(10)的研究成果,建立的综合考虑h和H的双因素路基当量回弹模量的预估方程,如式(11)。

表6 回归系数与H的对应关系

图5给出了预估方程的可靠性分析结果。由此可见,基于预估方程的ER预估值与理论计算值之间具有较高的相关性,进而表明所建立的双因素预估方程合理可靠。

3.4 E R预估结果可靠性分析

利用上述建立的预估方程,在实体依托工程中抽样选取5个代表性点位,进行了预估计算,并在对应位置的路表及路基顶面分别进行了FWD及承载板测试。观测月份地下水位距路表的距离为0.6 m,测点路基填高分别为1.2 m、2.2 m、3.8 m、5.4 m和6.5 m。ER预估值及测试值,如图6所示。

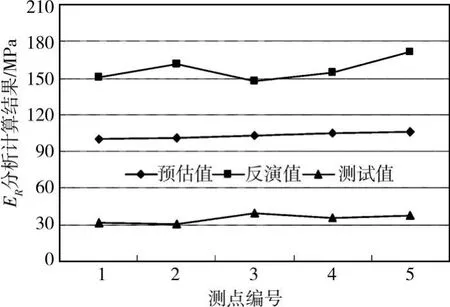
图6 不同分析方法的E R值对比

由此可知：不同点位上承载板测试静态值与FWD反演动态值之比处于0.19～0.27之间,均值为0.23;而承载板测试静态值与本文预估值之比处于0.31～0.38之间,均值为0.34。导致前者比值较低的主要原因在于FWD反演值过高,一般来说由于路基土具有应力依赖性,FWD加载中心点下路基的实际当量回弹模量值最小,而现阶段在利用FWD进行沥青路面各结构层模量反演分析时,所采用的各种分析软件(本文采用Evercalc 5.0)由于假设路基结构是弹性半空间体,这样反演得到的路基模量是一个综合值,其值远比FWD加载中心点下实际当量回弹模量值要大。相比而言,文中提出的预估分析方法充分考虑了荷载作用区域下路基土平衡湿度及应力状态对于ER值的影响,进而导致承载板测试结果与预估分析结果的比值与AASH TO (1993)提出的路基静动回弹模量之比为0.33的研究成果基本吻合[1],这充分验证了文中提出的ER预估分析方法及双因素预估方程合理可行。

4 结 论

基于非饱和土基本理论,通过室内外试验研究,集成创建了综合考虑路基平衡湿度和应力状态的路基当量回弹模量的预估分析方法,并结合实体依托工程,建立了路基顶面当量回弹模量的预估方程,具体研究结论如下：

1)水网密集区粘土路基的平衡湿度状态主要由地下水位控制,采用以路基相对高度为变量的土水特征曲线Fredlund&Xing模型可有效对粘土路基的平衡湿度进行预估。

2)在相同围压条件下,粘性土的动回弹模量随偏应力的增大而减小,表现了应力软化的特性,双线性动回弹模量预估模型可较好地解释其在不同湿度条件下的回弹特性。

3)将上述研究成果相耦合,集成创建了综合考虑路基平衡湿度和应力状态的路基当量回弹模量的预估分析方法,并结合实体工程,建立了以以地下水位、路基填筑高度为核心的路基当量回弹模量预估方程,试验路上不同测试方法的对比分析表明该评价方法及预估方程具有准确、可靠的特点。

4)研究成果为水网密集区粘土路基当量回弹模量的合理确定提供了新的视角和途径,具有现实的理论意义和工程实践价值。

[1]AASH TO Guide for design of pavement struc tures[S]. Washington DC：American Association of State Highw ay and Transportation O fficials,2002.

[2]杨树荣,拱祥生,黄伟庆,等.非饱和粘性路基土回弹模量之研究[J].岩土工程学报,2006,28(2)：225-229.

YANG SHU-RONG;GONG XIANG-SHENG,HUANG WEI-QING,etal.Resilientmodulus of unsaturated cohesive subgrade soils[J].Chinese Journal of Geotechnical Engineering,2006,28(2)：225-229.

[3]LI T,BA US R.Use of soil stiffness gauge for evaluatingmodulus ofgranular basematerials[C]//85th Annua lMeeting of Transportation Research Board(CDROM),2006.

[4]SUNIL SHARMA,AN IMESH DAS.Backcalculation of pavement layer moduli from falling weight deflectometer data using an artificial neural network[J].Can.J.Civ. Eng.,2008,35：57-66.

[5]BLATZ J,CU IY,OLDECOP L.Vapour equilibrium and osmotic technique for suction control[J].Geotechnical and Geological Engineering,2008,26(6)：661-673

[6]杨明,余飞.膨胀土路基毛细水上升规律及处置技术[J].中国公路学报,2009,22(3)：26-30.

YANG MING,YU FEI.Capillary water upw ard law and treatment technique of expansive soil subgrade[J]. China Journal of H ighw ay and Transport,2009,22(3)：26-30.

[7]曹长伟.路基湿度状况及模量调整系数研究[D].上海：同济大学,2007.

[8]BULUT R,LEONG E.Indirec t measurement of suction[J].Geotechnical and Geological Engineering, 2008,26(6)：633-644

[9]SOONK IE N,MARTE G,PANAYIOTIS D,et al. Comparison of testing techniques and models for establishing the SWCC of riverbank soils[J]. Engineering Geology,2010,110(1/2)：1-10.

[10]ZAPATA C,HOUSTON W,HOUSTON S,et al. Soil-water characteristic curve variability [C]// Proceedings of Sessions of Geo-Denver 2000,Advance in Unsaturated Geotechnics.Denver：University of Denver,2000：84-124.

[11]DAEHYEON K IM,JONG RYEOL K IM.Resilient behavior of compacted subgrade soils under the repeated triaxial test[J].Construc tion and Building Materials, 2007,21(7)：1470-1479.

[12]AASH TO.T292-91 Resilientmodu lus of subgrade soils and untreated base/subbase materials[S].USA：AASH TO Pub lications Department,1993.

[13]陈声凯,凌建明,张世洲.路基土动态回弹模量室内试验加载序列的确定[J].公路,2006(11)：148-152.

CHEN SHENG-KA I,LING JIAN-MING,ZHANG SHI-ZHOU.Fixing loading sequence for resilient modu lus test of subgrade soil[J].H ighway,2006(11)：148-152.

[14]THOMPSON M,ROBNETT Q.Resilientproperties of subgrade soils[J].Journal of T ransportation Engineering,1979,105：71-89.

[15]HUANG YANG H.Pavement analysis and design (second edition)[M].USA：Prentice H all,2003.

(编辑 王秀玲)

Prediction Analysis on Equivalent Resilient Modulus of Clay Subgrade ofWater Network Intensive Areas

QIUXin1,YANGQing1,QIANJin-song2

(1.College of Engineering,Zhejiang NormalUniversity,Jinhua,321004,P.R.China; 2.Traffic and T ransportation Engineering Institute,Tongji University,Shanghai,201804,P.R.China)

According to unsaturated soil basic theories,equilibrium moisture of clay subgrade is predicted based on the updated studiesof soil suction and soilwater characteristic curve.A lso,the bilinearity constitutive experience model of resilientmodu lus of clay soil is p resented by triaxial repeated loading tests in laboratory.Using abovementioned results,a prediction method of equivalent resilient modulus of clay subgrade is established by comprehensively considering subgrademoistureand stress condition.Then,based on the concreteengineering,the prediction function of equivalent resilientmodu lus of the clay subgrade is provided by taking ground water tab le and subgrade height as centers.Compared with the results of other traditional testing methodson the same test road, the new prediction method may be used in practice.The results provide new perspectives and standpoints to determine the equivalent resilient modu lus mechanics features of clay subgrade structure from two aspects of equilibrium moisture and stress condition.

clay subgrade,equilibrium moisture,resilientm odu lus,p rediction function

TU113

A

1674-4764(2011)02-0038-07

2010-07-11

国家自然青年科学基金项目(50908176)

邱欣(1978-),男,博士,主要从事路基路面结构力学行为与工程技术研究,(E-mail)xqiu@zjnu.edu.cn。