三边约束钢板的抗剪承载力
郭 震,袁迎曙
(中国矿业大学力学与建筑工程学院,江苏徐州 221008)
三边约束钢板的抗剪承载力
郭 震,袁迎曙
(中国矿业大学力学与建筑工程学院,江苏徐州 221008)
利用静力加载方法对4种宽厚比的三边约束钢板单元进行了试验研究,通过试验考察了三边约束钢板的破坏形态和抗剪极限承载力,分析了宽厚比对钢板抗侧性能的影响,试验结果表明:小宽厚比钢板的抗屈曲能力较强,但是对边界约束条件要求较高,易造成边界连接破坏。根据钢板破坏形态,对其抗侧性能进行了理论分析,建立了三边约束钢板的抗侧性能计算模型,给出了三边约束钢板极限抗剪承载力计算公式。文章最后对三边约束钢板的选择和设计提出了建议。
三边约束钢板;抗剪承载力;屈曲荷载;剪切屈服;边界条件;约束刚度
以钢板作为钢框架抗侧构件的钢板剪力墙结构体系始于20世纪70年代[1]。钢板以四边约束的形式嵌固于钢框架梁柱间,嵌固形式可以是高强螺栓连接,也可以采用焊接。早期的钢板剪力墙设计以弹性屈曲为极限状态,为防止钢板屈曲失稳,钢板较厚[2-3]。Basler[4]认为薄板失稳属于稳定分叉失稳,钢板屈曲后仍具有一定的后继强度承担外部荷载。1983年,Thorburn[5]等人首次利用屈曲后强度理论对薄型钢板进行了理论分析;随后,Tim ler和 Kulak[6]也利用试验手段验证了屈曲后强度理论。近年的研究结论表明:非加劲薄钢板剪力墙屈曲后形成的对角斜向拉力带仍然能够承担水平剪力,并且具有较好的经济性[7]。
国内外研究人员针对结构的抗侧特点和钢板受剪特征,对四边约束钢板剪力墙构造提出了多种改进形式。如,从优化结构耗能方面,提出了开竖缝式钢板剪力墙和两侧开缝钢板剪力墙(两边约束钢板)[8];从提高结构抗侧能力方面,提出了加劲钢板剪力墙[9];从改善钢板受力、防止钢板屈曲方面,提出了组合钢板剪力墙形式[10-11]。以上的改进方案均秉承一个原则:优化改善钢板单元抗侧性能,提高结构整体的抗侧能力和耗能能力。
参考短肢混凝土剪力墙和四边约束钢板剪力墙两者的受力特征,提出了适用于小高层建筑的新型钢板剪力墙结构体系[12],见图1所示。经过初步试验研究,该结构体系具有较好的耗能能力和滞回特性。然而,关于三边约束钢板剪力墙对钢框架抗侧性能的贡献、钢板自身抗剪承载力大小及三边约束钢板破坏形态和受力特征还尚未进行相关的研究。因此,深入研究三边约束钢板的受力特征、抗剪承载力及破坏形态是探索开洞式组合钢板剪力墙结构体系抗震性能的必要前提。论文提取剪力墙中三边约束钢板作为研究对象,针对4种不同宽厚比的三边约束钢板进行静力试验研究和理论分析,以揭示三边约束钢板的受力特征、抗剪承载力及破坏形态。

图1 钢框架中三边约束的钢板剪力墙示意图
1 试验设计
为获取三边约束钢板的屈曲模式、破坏特征、抗侧刚度及抗剪极限承载力,将通过静力加载方式对独立钢板进行试验研究分析。因为仅考察钢板自身的特性,所以试验采用铰接钢框架而忽略钢板周边框架节点的抗侧性能。
1.1 试件设计及分组
按照钢板宽厚比不同试件共有4个,试件P-1、P-2、P-3及P-4的钢板宽厚比逐次增大。试验用钢板为 Q235-B级钢,实测抗拉强度为256 MPa。钢板三个固接约束边预留孔距180 mm的Ø14圆孔,与加载框架的连接耳板用8.8级M12高强螺栓连接,螺栓预拉力为140 kN。四块钢板的自由边均焊接L40×3双拼等边角钢弹性约束。钢板有效高度均为h=1 100 mm,其他有效尺寸见表1。图2为钢板与加载框架耳板连接的示意图。
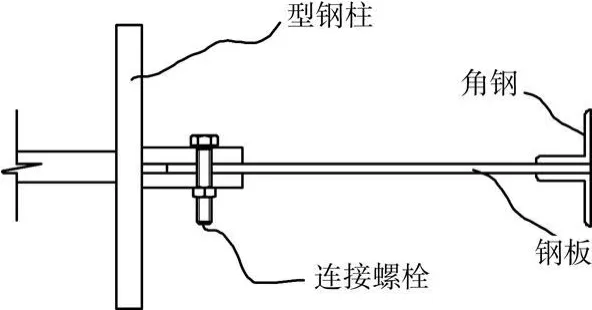
图2 钢板与加载框架连接方式
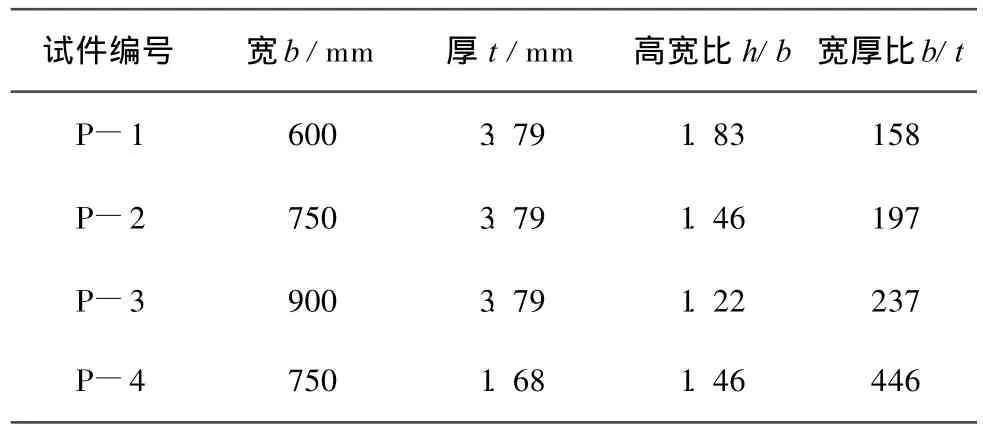
表1 试件分组及内嵌钢板有效尺寸
1.2 试验装置及加载机制
1.2.1 试验装置组成及作用 由于不考虑梁柱变形及梁柱节点刚度对钢板的影响,故试验装置为纯铰接框架,钢板采用相同的连接固定方式分别在同一加载框架内完成试验,试验加载示意见图3(a)所示。梁柱截面刚度远大于内嵌钢板屈曲刚度,采用焊接H型钢制作,梁柱截面均为H200×200×15× 15(mm),地梁截面为H 400×400×20×20(mm)。削去柱两端翼缘,将柱腹板插入钢梁预焊鱼尾板内,用M60销栓相连形成梁柱铰接节点。框架内部翼缘预焊20mm连接耳板,耳板开孔尺寸及间距与钢板对应。
1.2.2 试件安装 试验中,通过反力墙上水平液压伺服作动器铰接框架施加低周往复荷载,模拟水平荷载。加载位移由水平位移传感器量测,所有数据通过TDS303数字采集仪输入到电脑端。试验装置及加载情况见图3(b)。在铰接加载钢框架钢横梁施加平面外约束防止侧向失稳,加载框架地梁用地脚螺栓固定在地槽内,水平方向再与反力墙连接防止水平滑移。
1.2.3 加载制度 通过数值模拟预估各试件的屈服位移δy,以0.5δy,1.0δy,2δy,3δy,4δy, 5δy,6δy,7δy,8δy,9δy,10δy,11δy及12δy为位移加载级别,每级循环2次。当加载荷载降低到极限荷载85%时终止试验。
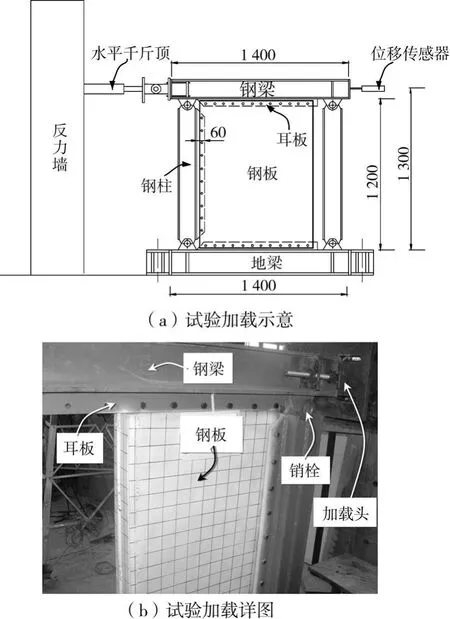
图3 试验加载情况
2 钢板墙体试验过程
2.1 钢板墙体抗力过程与破坏形态
2.1.1 小宽厚比钢板 试件P-1、P-2及P-3的钢板约束边均出现不同程度的螺栓滑移和破坏现象,说明这3个试件的钢板屈曲强度要高于边缘摩擦约束强度,边缘约束能力不足造成螺栓滑移和破坏。螺栓破坏位置及时机见图4和表2所示。螺栓的滑移和破坏导致钢板形成有效的抗剪面积减小,试验中加载荷载均有不同程度的降低。试件P-1螺栓破坏现象最严重,有4颗螺栓被剪断。试件P -1和P-2面外变形较小,当连接螺栓滑移停止后,即螺栓从摩擦型转变为承压型,钢板发生单波鼓曲变形。试件P-3钢板有对角线方向交叉屈曲的趋势。角钢扭曲破坏程度随着钢板宽厚比的增加不断减轻,靠近钢板上边缘的角钢仍旧保持初始形态,为发生变形。试件P-1破坏形态见图5。
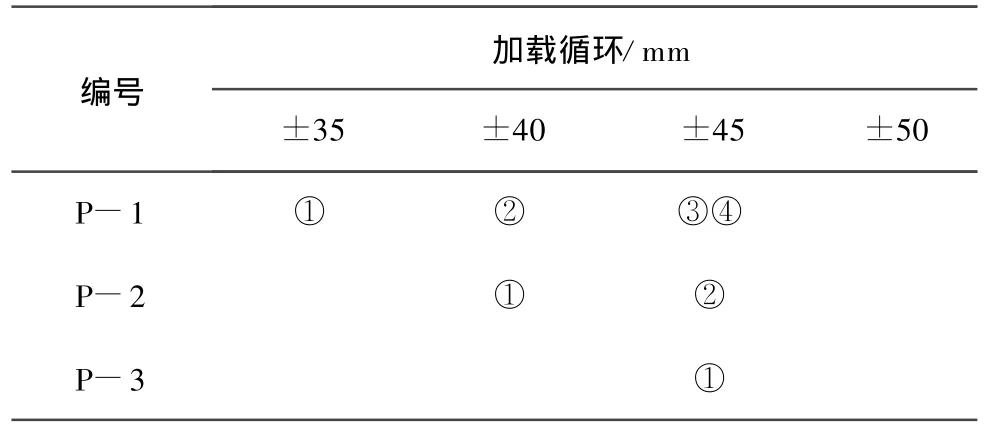
表2 螺栓破坏顺序

图4 钢板与耳板螺栓连接示意
2.1.2 大宽厚比钢板 试件P-4的钢板宽厚比较大,钢板的面外变形也最为严重。钢板对角线方向发生较为明显的交叉屈曲带,最终在交叉点钢板被撕裂。该钢板与耳板连接的螺栓未发生滑移和破坏现象。与试件P-1、P-2及P-3相比,角钢扭转变形量最小,在靠近钢板上边缘的角钢部分并未出现变形,说明角钢的弹性约束是有一定的有效长度的。钢板破坏情况见图6。

图5 试件P-1破坏形态

图6 试件P-4破坏形态
2.2 试件抗剪承载力分析
通过水平千斤顶处的荷载传感器获得试件的加载荷载,试件的水平加载荷载-层间位移角(P-θ)变化曲线见图7。
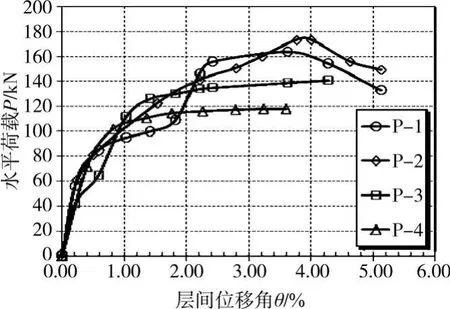
图7 抗剪承载力与层间位移角关系曲线
从图中可以看出:试件P-1、P-2及P-3的荷载-位移曲线较不规整,这是因为在试验过程中钢板与耳板间的连接螺栓破坏,造成钢板有效抗剪面积减小引起的;当螺栓破坏后,水平荷载的有一阶段增幅缓慢,随着面内应力重发布后钢板承载能力又有较大恢复。虽然这3个试件的初始抗侧刚度要高于P-4,但是对边界约束条件要求较高,否则易造成边界约束失效,钢板的材料性能也得不到应有的发挥,而影响整体的抗侧性能。
2.3 钢板剪力墙抗剪机理分析
不同宽厚比钢板的抗侧机理是不同的。根据钢板抗屈曲承载力与全截面抗剪承载力的关系,当其比值为1时,可以得到钢板临界宽厚比为143。
当钢板宽厚比小于143时,钢板的抗屈曲承载力要高于钢板全截面抗剪承载力,钢板将以材料破坏为主,这也是早期钢板剪力墙设计的依据。当钢板宽厚比大于143时,钢板将先发生屈曲失稳,但是它不同于受压构件屈曲,这种失稳属于稳定分叉失稳,也即是屈曲后仍具有较高的承载能力,具有薄板特征。文献[13]也论证了:钢板屈曲强度与截面屈服强度比值越小,钢板屈曲后强度发展也越充分。由于实际钢板的初始缺陷,当钢板几何特征为临界宽厚比时,屈曲失稳破坏的可能性最大,此时钢板承载力也已接近屈服承载力,钢板屈曲后的强度无法利用。
试验中采用的4种钢板试件的宽厚比均大于143,虽然抗侧机理相同,但是它们的破坏形态各异,说明钢板宽厚比及边缘约束能力决定了钢板的受力特征和破坏形态。
1)试件P-1及P-2 4种宽厚比的钢板在相同固结约束条件下,试件P-1和P-2的固结边约束发生螺栓滑移和剪断破坏;4种宽厚比的钢板采用相同的角钢弹性约束,试件P-1和P-2的角钢扭曲最为严重,说明试验选用的角钢型号对该级别宽厚比的钢板弹性约束能力有限。试件P-2的破坏程度要小于试件试件P-1。综上可以发现:
(1)属于薄板范畴的小宽厚比钢板在屈曲后,在拉力带尚未屈服时,过高的拉力场将使钢板的嵌固连接较早破坏,有效拉力带数量减少,钢板单元承载力不能充分发挥;
(2)小宽厚比钢板对弹性约束边的要求也较高,角钢约束能力的不足,也导致钢板面内有效拉力场面积较小,见图8(a)和(b),钢板屈曲后的自身塑性得不到有效发展。
2)试件P-3及P-4试件P-3钢板的宽厚比虽小于试件P-4,但前者的破坏形态已与小宽厚比试件(P-1和P-2)有了较明显区别,角钢扭转变形减小,连接螺栓破坏程度减轻。试件P-3及P-4的钢板表现出了屈服和屈曲同时存在特点。以试件P-4为例,钢板先是面外屈曲,而后屈服;屈服发展的过程中,亦存在对角线拉伸屈服和边缘剪切屈服;钢板的面外变形也最为严重。
3 三边约束钢板的力学分析
三边约束钢板墙体利用角钢限制钢板自由边的面外屈曲,使内嵌钢板成为三边固结,一边弹性约束的纯剪板。弹性约束边尚有转动的可能性,其约束性能介于刚性固结与简支之间。Thorburn[5]认为弹性边界对钢板屈曲后拉力带的形成没有帮助,可以忽略弹性约束边的影响,建议采用Basler[4]提出的等效桁架模型,见图8(a)。
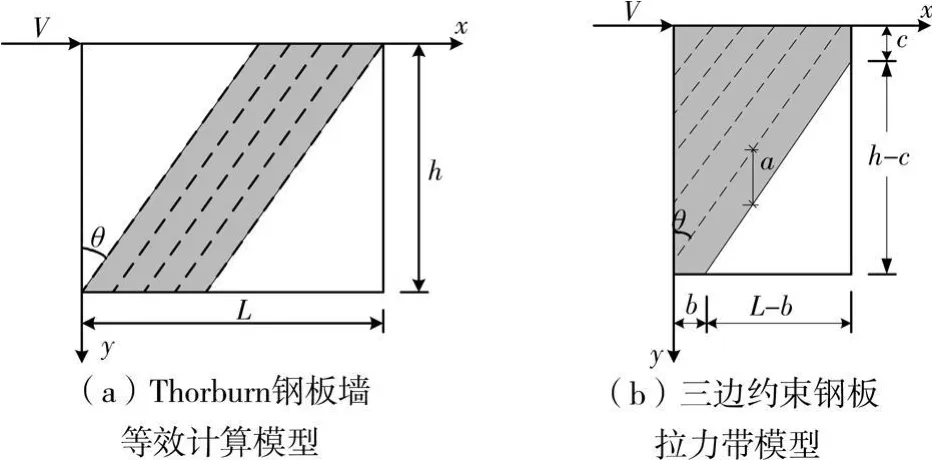
图8 钢板墙单元等效模型
然而通过试验发现,角钢对钢板斜向拉力带的形成还是有一定贡献的,见图8(b)所示阴影区,角钢的有效约束长度为c。
3.1 屈曲阶段
如果钢板屈曲强度τcr小于钢材的比例极限,那么钢板将发生弹性屈曲失稳,大宽厚比钢板(λ>400)属于此类情况。弹性阶段仍可以采用薄板理论进行分析,此阶段的最大抗剪承载力为屈曲荷载,通常情况下,钢板宽厚比越大,钢板的屈曲荷载越小。

9 钢板平面应力分析简图
钢板的失稳破坏特征是钢板中部对角斜向单波屈曲。当钢板平面内剪应力在某一方向形成的主压应力σc达到屈曲强度时,钢板发生单波鼓曲,该方向已不能继续承受压力,如图9。然而在垂直于主压应力的方向将形成斜向拉力带,沿波棱线方向钢板继续承受对角线方向拉力,超出屈曲荷载的水平荷载增量沿拉力带方向的分量由拉力带承担。
3.2 屈曲后阶段
钢板屈曲后,可以认为σc增量等于零,由斜向拉力带承担水平剪力,但是由于角钢弹性特点,钢板能够形成拉力带的区域见图8(b)阴影部分。在该区域内,σt逐渐达到屈服强度,钢板最终受拉屈服破坏。同时从图中也能看出,角钢在钢板屈曲后对钢板屈曲后继强度的发展及有效承载面积起到了重要作用。
4 三边约束钢板抗剪极限承载力计算模型
4.1 钢板屈曲临界状态
角钢在钢板屈曲前起到了弹性约束的作用所以钢板屈曲时的抗剪承载能力是钢板屈曲临界承载力,仍然可以用经典薄板理论的解析解求出。
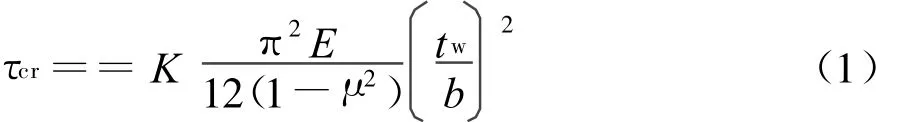
式中,b为钢板宽度,mm为钢板厚度,mm;τcr为钢板临界屈曲应力,MPa为钢材弹性模量,MPa,K为弹性屈曲系数,令钢板宽高比α=L/h,则K=
钢板屈曲临界承载力Vcr为

4.2 钢板屈曲后状态
钢板屈曲后,角钢有效约束长度为c,见图8 (b),钢板能够发展屈曲后继强度的区域为虚线部分。假定钢板的斜向拉力带均匀分布,则每条拉力带y向宽度为a,拉力带与边界夹角为θ,对于四边约束钢板,Driver[14]与Elgaaly[15]认为该拉力带倾角约为45°。
图10 钢板与角钢计算简图
从图8(b)可知:

根据图10(a)可知:

当σt达到极限强度时,钢板达到屈曲后极限抗剪承载力。因此,三边约束、一边弹性约束钢板的极限抗剪承载力Vu为
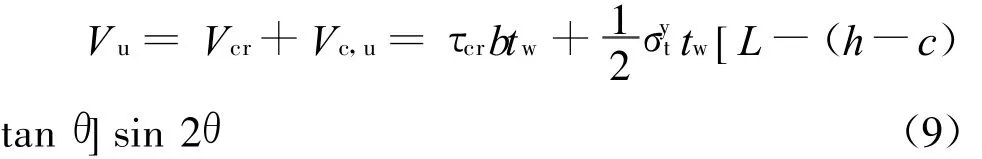
按图10(b)所示机构,采用机动法可求出c,

式中,c为弹性边有效约束长度为有效边缘构件的塑性弯矩,钢板屈服强度。
根据图8(b)所示,当柱顶施加水平剪力V时,三边约束钢板屈曲后,正应力在有效的拉力场做功为:
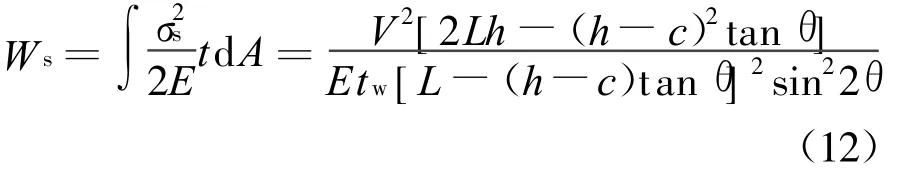
式中A为图8(b)所示阴影区域的面积。当/∂θ=0时存在极大值,以β=L/h和γ=c/h为考察参数,可以得到:

根据式(13),可以绘制图11所示的c/h与倾角θ的关系,分别选取试验的钢板宽高比1.22,1.46及1.83进行对比分析。从图11中可以看出,当c/h在0~1之间变化时,钢板拉力带与竖向边缘构件的夹角最大为45度,也即说明无论钢板与边缘构件间约束为何种形式,水平剪力使钢板产生的拉力带与边缘构件间夹角最大为45度。还可以看出,钢板倾角的大小仅与钢板高宽比及角钢有效约束长度有关,与钢板厚度或宽厚比无关。
图11 与倾角θ的关系根据图11曲线可以得到角度的简化计算公式:
θ=θ0+(45-θ0)(c/h)3(14)式中,θ0为c/h=0时,钢板斜向拉力带与y向的夹角,即为无角钢约束的情况。
4.3 钢板抗剪承载力计算与试验结果比较分析
计算结果与试验结果对比见表3,表中计算结果采用式(9)和(14)求得。
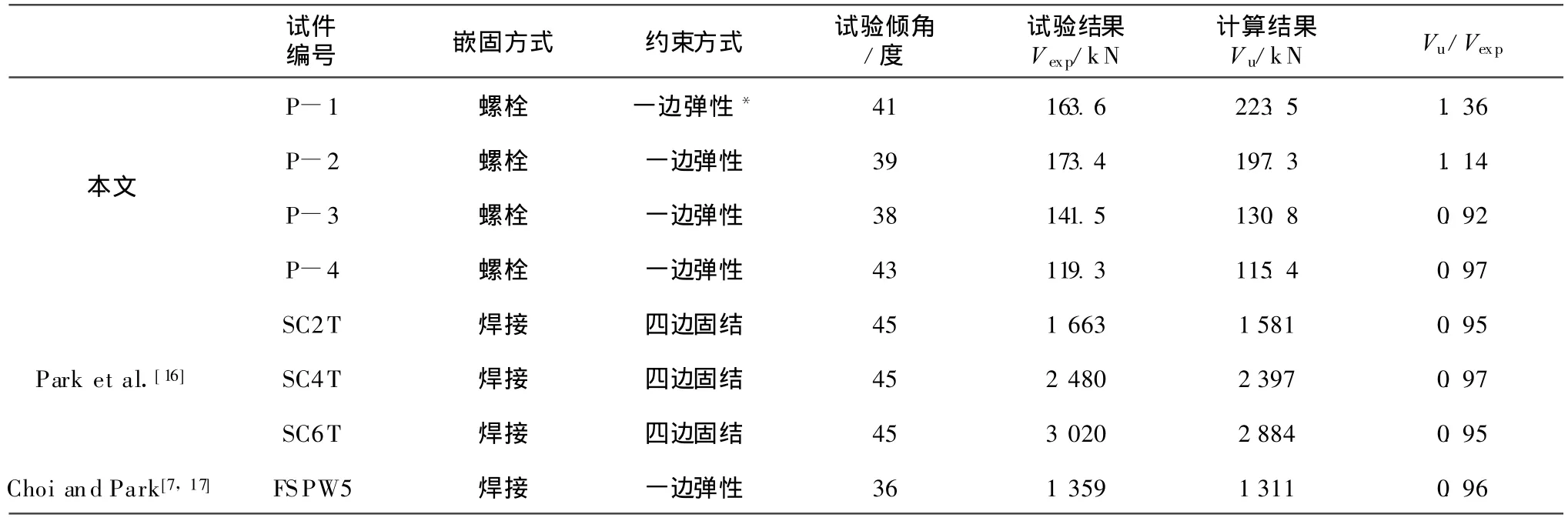
表3 计算结果与实验结果对比
表3中的计算与试验比较结果反应了理论分析假定及公式简化推导的方法是可行的。从试验现象和数据分析上看,具有较大宽厚比的三边约束、一边弹性约束钢板(P-3和P-4),其试验结果与理论计算结果吻合较好,能够采用本文提出的计算公式,相应的力学模型亦能够对其进行相关理论分析。试件P-1和P-2的试验结果与计算结果偏差较大,这是因为在试验中,钢板与边缘框架连接破坏,嵌固作用丧失,导致钢板无法充分发展材料性能。
5 结 论
针对4种不同宽厚比的三边约束钢板进行了试验研究和理论分析,通过试件的破坏特征和试验结果,建立了理论分析模型并提出了三边约束钢板的极限抗剪承载力公式,为深入研究开洞式组合钢板剪力墙结构体系的抗侧性能提供了必要的理论基础。试验和理论分析结果表明:
1)三边约束钢板的承载力除了与自身宽厚比有关外,还与弹性约束边的角钢约束能力有关,当角钢型号越大,即有效约束长度c越长,钢板承载能力发挥越充分。
2)小宽厚比三边约束钢板抗屈曲能力较强,抗剪承载力也较高,但是钢板面内的较高拉力场也对边缘约束能力有较高的要求。边缘约束是保证钢板屈曲后充分发挥材料性能的重要条件,根据式(7)可以求得钢板与耳板间的最小连接强度,选择合理的连接措施,以保证边缘约束不破坏。但是,钢板宽厚比越小,边缘连接强度要求越大,从施工难易程度和材料用量的方面来看是不适宜的。
3)大宽厚比三边约束钢板虽然抗剪承载力不高,但是对边缘约束的要求亦不高。当采用相同的角钢弹性约束时,相对于小宽厚比三边约束钢板来说,大宽厚比三边约束钢板屈曲后有效受力面积最大(见图8(b)),钢板材料也能够得到最大的发挥。
4)理论分析结果与试验结果较为吻合,说明理论分析假定及公式简化推导是合理的,理论计算方法是可行的。文中提出的三边约束钢板的极限抗剪承载力公式、计算模型和倾角简化公式可以为三边约束钢板的设计和研究提供较好的帮助。
5)根据前面的总述,三边约束钢板的抗侧刚度、延性性能、耗能能力及边界约束设计将是进一步重点研究的内容。通过对比分析不同宽厚比的三边约束钢板延性性能、耗能能力和边界约束设计,最终提出适用于开洞式新型组合钢板剪力墙结构体系的合理的三边约束钢板宽厚比及构造措施。
[1]郭彦林,董全利.钢板剪力墙的发展与研究现状[J].钢结构.2005,20(77):1-6.
GUO YAN-LIN,DONG QUAN-LI.Research and app lication of steel p late shear w all in high-rise buildings[J].Steel Structural,2005,20(77):1-6.
[2]SABOURI-GHOMI SAEID,VEN TURA CAROS E, KHARRAZIMEHDI H.Shear analysis and design of ductile steel p late walls[J].Journal of Structural Engineering,2005,131(6):878-889.
[3]SABELLI RAFAEL BRUNEAU,MICHEL DRIVER, ROBERT G.Steel plate shear w alls in the upcom ing 2010 A ISC seism ic provisions and 2009 canadian standard S16[C]//Crossing Borders,Vancouver,BC, Canada:ASCE,2008.
[4]BASLER K.Strength of plate girders in shear[J]. ASCE Journalof the Structural Division,1961,87(7):150-180.
[5]THORBURN L J,KULAK G L,MONTGOMERY C J.Analysis of steel p late shear walls[R].Structural Engineering Report No.107.Department of Civil Engineering, Universtiy of A lberta, Edmonton, A lberta,Canada.1983.
[6]TIMLER P A,KULAK G L.Experimental study of steel p late shear w alls[R].Structural Engineering Report No.114.Department of Civil Engineering, University of A lberta, Edmonton, Alberta, Canada.1983.
[7]LOVE R.JAY YU KENT,MCNEILL SEAN,et al. Retrofit of a critical care facility in los angeleswith steel plate shear walls[C]//Crossing Borders.Vancouver, BC,Canada:ASCE,2008.
[8]钟玉柏,张素梅,马欣伯.四边简支开缝钢板剪力墙抗剪静力性能研究[J].哈尔滨工业大学学报,2006,38 (12):2054-2059.
ZHONG YU-BA,ZHANG SU-ME,MA XIN-BO. Research of shear resistance static behaviors of steelplate shear walls with slits[J].Journal of Harbin institute of Techno logy,2006,38(12):2054-2059.
[9]郭彦林,陈国栋,缪友武.加劲钢板剪力墙弹性抗剪屈曲性能研究[J].工程力学,2006,23(2):84-91. GUO YAN-LIN,CHEN GUO-DONG,MIAO YOUWU.Elastic buck ling behavior of steel p late shear wall w ith cross or diagonal stiffeners[J].Engineering Mechanics,2006,23(2):84-91.
[10]ZHAO QIU-HONG,ASTANEH-ASL A.Experimental and analy tical studies of a steel p late shear wall system[C]// Crossing Borders,Vancouver,BC,Canada:ASCE,2008.
[11]郭彦林,董全利,周明.防屈曲钢板剪力墙滞回性能理论与试验研究[J].建筑结构学报,2009,30(1):31-47.
GUO YAN-LIN,DONG QUAN-LI,ZHOU MING. Tests and analysis on hysteretic behavior of bucklingrestrained steel p late shear w all[J].Journalof Building Structures,2009,30(1):31-47.
[12]郭震,袁迎曙.短肢钢板剪力墙构造形式研究[J].建筑结构,2010,40(2):40-44.
GUO ZHEN,YUAN YING-SHU.study on structure form of short pier steel plant shear walls[J].Building Structures,2010,40(2):40-44.
[13]王迎春,郝际平,李峰,等.钢板剪力墙力学性能研究[J].西安建筑科技大学学报:自然科学版,2007,39 (2):181-186.
WANG Y ING-CHUN,HAO JI-PING,LIFENG,et al. Study on mechanical p roperty of stee l p late shear wa lls [J].J.Xi'an Univ.of A rch.&Tech:Natural Science Edition,2007,39(2):181-186.
[14]SH ISHKIN JONAH,JDRIVER,ROBERT G,et al, Gilbert Y.Analysis of steel p late shear walls using the modified strip model[J].Journal of Structural Engineering,2009,1(1):33-33.
[15]ELGAALY M.Post-buckling behavior of thin steel plates using computational models[J].Advances in Engineering Software,2000,31(8/9):511-517.
[16]PARK HONG-GUN,KWACK JAE-H YUK,JEON SANG-WOO,et a l.Framed steel p late w all behavior under cyclic lateral loading[J].Journal of Structural Engineering,2007,133(3):378-388.
[17]CHOI IN-RAK,PARK HONG-GUN.Steel p late shear w alls with various in fill p late designs[J].Journal of Structural Engineering,2009,135(7):785-796.
(编辑 王秀玲)
Shear Performance of Steel Platew ith Trilateral Constrained
GUOZhen1,YUANYing-shu
(Schoolof Mechanics&Civil Engineering,China University of Mining and Technology,Xuzhou 221008,P.R.China)
The load carrying test for four steel p late shear walls specimens w ith various ratio of w idththickness are carried out so as to test the failure mode and the shear strength of steel p late w ith trilateral constrained,and the lateral stiffness and the buck ling mode are investigated in the test.The resu lt indicates that the ratio of width-thickness of steel p late exerts effects on the shear-carrying capacity and failuremode;the buckling of steel p late does not have lateral stiffness.Based on the failuremode of steel plate,the computation m odel of lateral perform ance is p resented by theoretical analysis.The restraining stiffness of double angle and the buck ling-restrained stiffness of steel p late are the important design conditions.Formu lae to determ ine the elastic lateral stiffness and the angle type is p roposed,which can be used in the preliminary design of steel p latew ith trilateral constrained.
Steel p latew ith trilateral constrained;shear strength;buck ling-load;shear yielding;boundary conditions;restraining stiffness
TU 312
A
1674-4764(2011)02-0051-07
2010-06-28
国家自然科学基金(50538070,50878207);中国矿业大学青年科研基金(2008A 009)
郭震(1978-),男,博士生,主要从事新型钢结构体系抗震研究,(E-mail)guozhen@cum t.edu.cn。
book=57,ebook=26

