滑坡灾害典型受灾体失效概率计算方法及应用
吴 越,刘东升,陆 新,宋强辉
(1.解放军后勤工程学院建筑工程系,重庆 400041;2.重庆市地质矿产勘查开发局,重庆 400039)
滑坡灾害典型受灾体失效概率计算方法及应用
吴 越1,刘东升2,陆 新1,宋强辉1
(1.解放军后勤工程学院建筑工程系,重庆 400041;2.重庆市地质矿产勘查开发局,重庆 400039)
从系统研究的角度看,滑坡灾害系统包括致灾体子系统和受灾体子系统。滑坡灾害是这2个子系统共同作用的结果。以往的研究主要集中在致灾体稳定性的评价上,没有全面考虑2个子系统对灾害风险的影响,尤其缺少对受灾体子系统的研究。针对这种现状,对一种典型受灾体(框架结构)在滑坡灾害作用下的失效概率计算方法进行探讨:将滑坡灾害致灾模式简化为致灾体对受灾体的冲击破坏模型,推导了滑坡冲击力计算公式;探讨了典型受灾体整体功能函数的建立方法,提出了滑坡灾害典型受灾体失效概率计算方法。采用该方法进行了算例分析,分析了滑坡灾害致灾强度和受灾体抗灾性能对受灾体失效概率的影响,得出滑坡灾害影响范围可划分为绝对危险区域、相对危险区域和绝对安全区域。还研究了受灾体失效概率对不确定性影响因素的敏感性,得出当定值计算受灾体为失效时,受灾体失效概率随影响因素变异性增加而减小;当定值计算受灾体为安全时,受灾体失效概率随影响因素变异性增加而增加。
滑坡灾害;滑坡灾害受灾体;结构可靠度
滑坡灾害是指岩土体在重力作用下沿一定的软弱结构面下滑而造成人类生命财产毁损的灾害事件[1]。滑坡灾害具有不可避免性[2],每年造成损失数十亿甚至上百亿,为此投入了大量的经费进行治理[3]。从系统研究的角度看,滑坡灾害系统包括致灾体子系统和受灾体子系统,滑坡灾害是这两个系统共同作用的结果[4](图1)。但以前的研究都只限于对滑坡体稳定性的研究,着重考察的是滑坡形成机制和诱发条件,度量的指标多是稳定性系数、稳定性程度。从这些角度的研究固然必不可少,但防治滑坡灾害的最终目的不是杜绝引起灾害的这种地质现象的发生,而是确保这些地质现象不对人类造成不可接受的危害[5]。由图1可见,受灾体处于不同位置时,致灾强度是不同的;对于不同的受灾体而言,抗灾性能也是不同的;而滑坡灾害风险是受这两个方面因素影响的[6-8]。显然只研究滑坡体的稳定性是不全面的。因此有必要将滑坡灾害致灾体和受灾体作为一个系统来研究,尤其需要加强对受灾体子系统的研究。
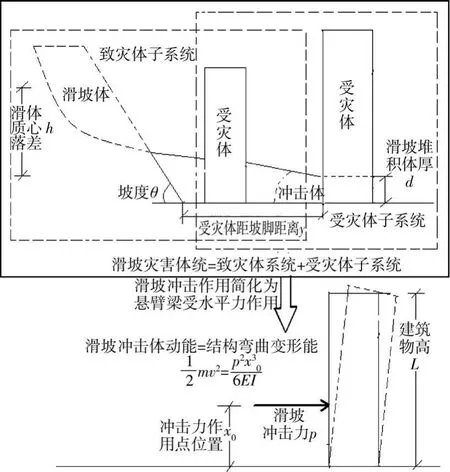
图1 滑坡致灾过程简化图
为此,对一种典型滑坡灾害受灾体(框架结构)在灾害作用下的失效概率计算方法进行探讨研究:将滑坡致灾模式简化为致灾体对受灾体的冲击破坏模型,并推导滑坡冲击力的计算公式。然后建立受灾体整体功能函数,将滑坡冲击力作为荷载,采用Monte Carlo法计算受灾体在滑坡冲击作用下的体系可靠度,并将该方法应用于算例分析。首先分析了致灾强度与受灾体相对位置的关系,然后又分析了致灾强度和受灾体抗灾性能与受灾体失效概率的关系,最后还分析了受灾体失效概率对不确定性影响因素的敏感性。全面考虑了滑坡灾害致灾体子系统和受灾体子系统对灾害后果的影响,为进一步的滑坡灾害风险定量评估提供基础。
1 受灾体失效概率计算方法
滑坡灾害根据受灾体相对致灾体的位置,可分为2种工况:1种是受灾体处于滑坡体上,该工况下,一旦发生坡体失稳,受灾体失效概率将为100%;另1种工况受灾体不在滑坡体上,而是处于滑坡体滑动影响范围内,该工况下受灾体失效概率与其所处位置及其抗灾性能相关。因此重点研究第2种工况下的受灾体失效概率。
如图1所示的滑坡模型属于第2种工况,此时滑坡灾害破坏模式主要是致灾体对受灾体的冲击破坏,为了便于计算将其简化为水平集中力对结构的变形破坏作用。此时受灾体失效概率的计算需要解决2个问题:1)如何计算滑坡冲击力;2)如何建立受灾体整体功能函数。
1.1 滑坡冲击力计算方法
如图1所示,将滑坡冲击作用简化为悬臂梁受水平推力的作用。结构弯曲能W可表示为[9]:

其中p为水平力,为结构弹性等效侧向刚度。
结构弹性等效侧向刚度EJd,可近似按倒三角形分布荷载作用下结构顶点位移相等的原则,将结构的侧向刚度折算为竖向悬臂受弯构件的等效侧向刚度。假定倒三角形分布荷载的最大值为q,在该荷载作用下结构顶点质心的弹性水平位移为,房屋高度为L,则结构的弹性等效侧向刚度可按下式计算[10]:

在实际计算时,先假设1个作用在结构侧向的倒三角形分布的荷载,其中最大值为q,然后采用有限元法计算出该荷载下结构顶点质心的水平位置,最后根据式(2)即可得到。
根据能量守恒定律:


根据简化的滑坡动力学模型[11]:
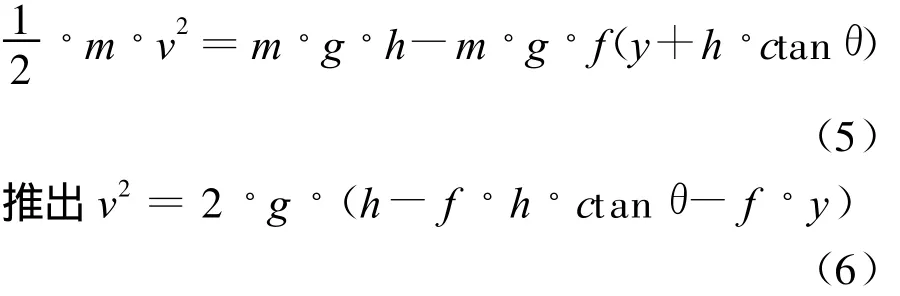
将式(6)带入式(4)得:
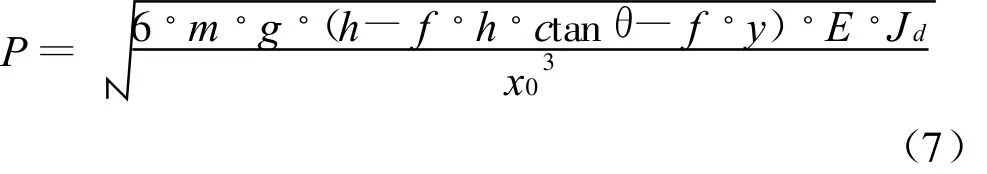
式中h为滑体质心落差;f为坡面摩擦系数;θ为坡角,y为受灾体到坡脚的距离。
在已知滑坡体及滑动路径参数的情况下,根据式(7)即可计算出滑坡冲击力。而在实际工程中,充满了不确定性,对于岩土工程而言,参数的随机不确定性对计算结果有很大影响[12-13]。因此有必要考虑随机性的影响。由于结构随机性与岩土随机性相比较小,坡高、坡角的随机性也较小,因此只考虑滑动路径摩擦系数f和堆积体厚度d的随机性。
1.2 受灾体整体功能函数的建立
受灾体失效概率属于体系可靠度的研究范畴,其关键是如何建立整体功能函数。虽然与构件可靠度的计算技术相比,体系可靠度的计算方法还不算成熟,但也是有很多研究成果可以借鉴,秦荣在文献[14]中对框架结构采用屋顶水平位移建立功能函数。文献[15]中也将结构水平位移作为衡量框架结构整体稳定性的指标。
受灾体在滑坡冲击作用下主要表现为水平的变形破坏,《高层建筑混凝土结构技术规程》对混凝土结构建筑的水平位移限值进行了规定,采用层间位移与层高之比(简称层间位移角)作为控制指标:

式中ϑi为第i层层间位移角;ui为第i层水平位移;高度不大于150m的常规高度高层建筑的整体弯曲变形相对影响较小,层间位移角△u/h的限值按不同的结构体系在1/550~1/1 000之间分别取值。但当高度超过150m时,弯曲变形产生的侧移有较快增长,所以超过250m高度的建筑,层间位移角限值按1/500作为限值。150~250 m之间的高层建筑按线性插入考虑。由于高层建筑结构在水平力作用下几乎都会产生扭转,所以△u的最大值一般在结构单元的尽端处[7]。因此受灾体整体可靠度的功能函数可以表示为:

式中ϑ*为结构允许的最大层间位移角;ϑmax为在荷载作用下最大的层间位移角。
功能函数小于零的概率及为特定滑坡破坏概率下受灾体失效概率:

这是假设滑坡体发生破坏情况下的失效概率,如果考虑坡体体的失效概率,则受灾体失效概率等于坡体失效概率与Pf的乘积。
2 算例分析
对图1所示的滑坡作用下受灾体失效概率进行计算分析,坡高h=40 m、滑体厚D=12 m,坡角θ= 45°、滑体土体密度ρ=1 900 kg/m3。滑坡路径摩擦系数f服从均值为1,变异系数为0.2的正态分布,滑坡堆积体厚度d服从均值为4 m,变异系数0.2,的正态分布。受灾体为5层钢筋混凝土框架结构,为跨宽5.4 m,层高4m,模型见图2,冲击力沿y轴方向。
2.1 计算及结果精度分析
以受灾体距坡脚距离y=14 m处为例简述计算过程:
首先建立受灾体有限元分析模型,柱和梁单元采用BEAM4、楼板单元采用SHELL63。根据式(7)将滑坡冲击力计算公式参数化,并将冲击力施加到结构模型上,在定值情况下进行求解。提取各层水平位移,并参数化。定值情况下结构水平位移见图2。然后按(9)式建立功能函数Z。

并采用Monte Carlo模拟10 000次。得出结构此时所受滑坡冲击力(图4),=0.621 924。若坡体失稳概率为0.7,则受灾体失效概率为0.435 346 8。
其它工况均可采用以上方法计算得到。
结构建模采用弹性梁单元,没有考虑塑性变形的影响,按弹性进行有限元求解。文献[10]中关于建筑物水平位移限值规定的目的就是保证主体结构基本处于弹性受力状态,因此将结构模型建立为弹性模型是合理的。

图2 结构在滑坡冲击作用下水平位移云图
另外需要说明的是,采用弹性模型计算是,结构所受荷载与变形线性相关,也可采用荷载作为标准来建立功能函数,结果是相同的。但需要将位移限值换算成荷载限值,且同样需要进行Monte Carlo模拟。
对于Monte Carlo法而言,模拟次数对计算结果有一定影响,但随着模拟次数的增加,结果会趋于稳定。图3是功能函数Z的样本均值与Monte Carlo模拟次数的关系曲线,图中3条曲线的含义是:中间曲线表示Z的均值,上下2条曲线是置信水平为95%时样本均值置信区间的上下限。反映了Monte Carlo模拟次数带来的误差。随着模拟次数的增加样本均值波动逐渐减小,趋于水平直线,置信区间也逐渐减小,当模拟次数达到10 000次时,3条曲线基本重合,表明此时由于样本数量带来的误差很小,可见10 000次Monte Carlo模拟是合理的。
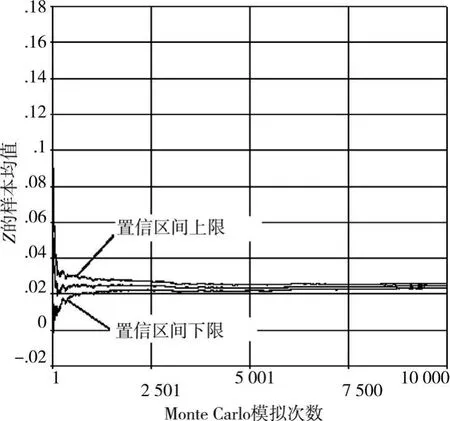
图3 样本均值与Monte Carlo模拟次数
2.2 滑坡冲击力及影响因素分析
考虑滑坡堆积体厚度和滑动路径摩擦系数的随机性,则特定结构在特定位置所受滑坡冲击力p是一个随机函数。图4是受灾体距坡脚14 m处滑坡冲击力的概率分布情况,图中滑坡冲击力为零的概率为0.027,是由于滑动路径摩擦系数的变异性引起,当摩擦系数较大时,滑坡体不能到达建筑物所处位置,不会形成冲击作用。可见图4中滑坡体有2.7%的概率不能到达建筑物所处位置。

图4 滑坡冲击力概率分布图
根据定性的认识,随着受灾体距滑坡源距离的增加,滑坡冲击力将逐渐减小。该文的计算结果符合这一规律。图5是受灾体处于不同位置时所受滑坡冲击力均值的变化曲线,可见计算方法是合理的。

图5 滑坡冲击力
2.3 致灾强度及抗灾性能对失效概率的影响
通过前面的分析和计算表明受灾体失效概率受到多种因素的影响,可以将影响因素分为2大类:
1)致灾强度因素:这里指滑坡冲击力。根据前面的分析可见,影响滑坡冲击力的因素主要是受灾体距滑坡源的距离。图6给出了受灾体失效概率随距离的变化规律。
由图6可见,受灾体失效随距离的增加而减小。0~9 m的范围失效概率为1,为绝对危险区域;9~25m范围内失效概率1~0之间,为相对危险区域;>25 m时失效概率为0,为绝对安全区域。
2)受灾体抗灾性能因素:这里指结构抗水平冲击的性能。采用等效侧向刚度作为衡量指标。分别计算了3种钢筋混凝土结构和3种钢管混凝土结构的失效概率,对应的整体等效侧向刚度按式(2)计算得到。
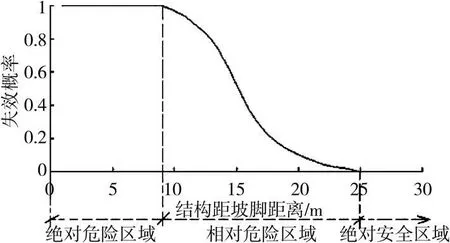
图6 失效概率与距坡脚距离
图7是同一致灾强度下(距滑坡源14 m处)受灾体失效概率与等效侧向刚度的关系。由图7可以得出以下结论:
1)框架结构材料和框架结构的跨数都会影响结构的等效侧向刚度。相同材料的跨数越多刚度越大;相同跨数的钢管混凝土比钢筋混凝土侧向刚度大。
2)等效侧向刚度越大受灾体失效概率越小,反之亦然。
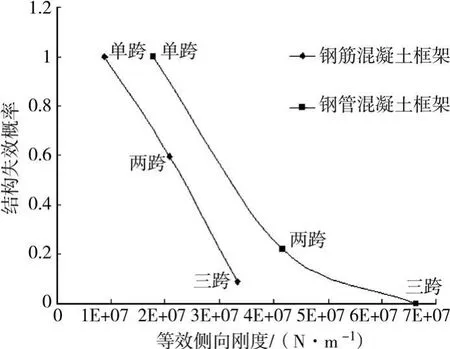
图7 失效概率与抗灾性能
2.4 不确定性因素对失效概率的影响
不确定性是岩土工程和结构工程中固有性质,尤其是岩土工程中的参数的随机不确定性对计算结果有较大影响。因此有必要对这些不确定参数对受灾体失效概率的影响进行分析。由于岩土随机性比结构随机性大得多,计算中只考虑了影响滑坡致灾强度的随机因素,即滑动路径摩擦系数f与滑坡堆积体厚度d的随机性。
分析受灾体对不确定性因素的敏感性,即分析不确定性因素变异性对失效概率的影响。计算结果表明(图8):当定值计算结构失效时,随着影响因素变异性增加失效概率逐渐减小;当定值计算结构安全时,随着影响因素变异性的增加,失效概率逐渐增大。另外失效概率对f的敏感性比d的大。需要说明的是:由于定值计算不考虑参数的随机性,其计算结果只是功能函数Z的均值。因此定值计算结构为失效时,只表明Z的均值小于零,失效概率大于50%。而定值计算结构安全时,也只表明失效概率小于50%,正是可靠度方法优于定值方法之处。
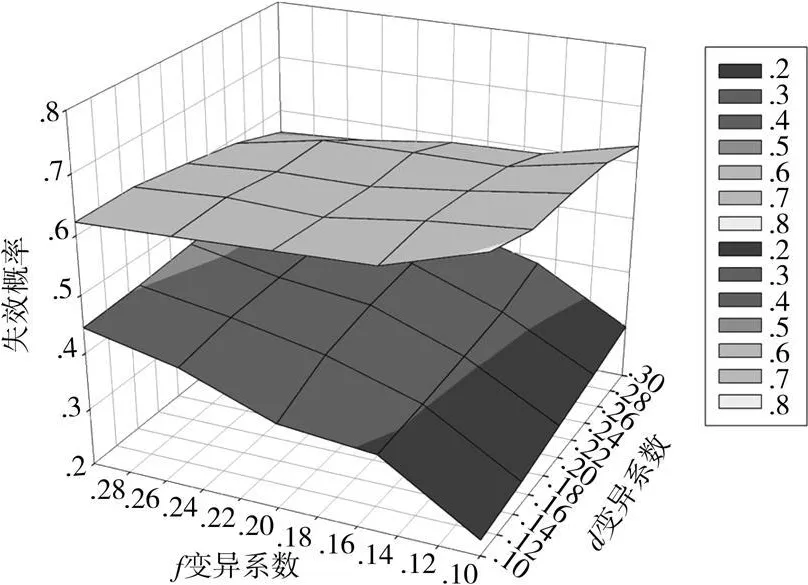
图8 受灾体失效概率影响因素敏感性图
以上结论的原因是(图9):功能函数Z均值小于0时,对应的失效概率大于50%,变异性增加使小于0的面积减小,则失效概率减小,但不会低于50%;功能函数Z的均值大于0时,对应失效概率小于50%,变异性增加使小于0的面积增大,则失效概率增加,但不会高于50%。

图9 变异性对失效概率的影响
3 结 论
针对目前对滑坡灾害受灾体研究较少的现状,将滑坡致灾体与受灾体作为一个体系进行研究。推导了滑坡冲击力计算公式,探讨了受灾体整体功能函数的建立方法,提出了滑坡灾害典型受灾体失效概率计算方法。
将该方法应用于算例分析,结果表明:滑坡冲击力随距离增加而减小;结构失效概率随滑坡冲击力增加而增加,随结构等效侧弯刚度增加而减小,反之亦然。当定值计算结构为失效时,随着影响因素变异性增加失效概率逐渐减小;当定值计算结构为安全时,随着影响因素变异性的增加,失效概率逐渐增大。另外根据结构失效概率与结构据滑坡源距离的关系,滑坡灾害影响范围可划分为:绝对危险区域、相对危险区域和绝对安全区域。
[1]AGS.A national landslide risk management framew ork for Australia,Australian geomechanics society[J]. Australian Geomechanics,2007,42(1):1-12.
[2]黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007.26(3):434-453
HUANG RUN-QIU.Large-scale landslide and their slidingmechanism s in China since the 20THcentury[J]. Chinese Journal of Rock Mechanics and Engineerine, 2007.26(3):434-453.
[3]李东升,刘东燕.边坡防灾工程风险决策分析[J].重庆大学学报:自然科学版,2005,28(12):104-107.
LIDONG—SHENG,LIU DONG-YAN,Risk Decision—making method of slope resistant engineering[J]. Journal of Chongqing University:Natura l Science Edition,2005,28(12):104-107.
[4]谢权敏,边翔,夏元友.滑坡灾害风险评价的系统分析[J].岩土力学.2005,26(1):71-74.
XIE QUAN-MIN,BIAN XIANG,XIA YUAN-YOU. Systematic analysis of risk evaluation of landslidehazard [J].Rock Mechanics,2005,26(1):71-74.
[5]向喜琼,黄润秋.地质灾害风险评价与风险管理[J].地质灾害与环境保护,2003,11(1):38-41.
XIANG X I—QIONG.HUANG RUN-QIU.Risk assessment and risk mangement for slope geohazards [J].Journal of Geologlcal Hazards and Environment Preservation,2003,(1):38-41.
[6]MIRCO,GALLI,FAUSTO.GUZZETTI,et al.Landslide vulnerability criteria:A Case Study from Umbria,Central Italy[J].Environ Manage,2007,40:649-664.
[7]KAYN IA.Probabilistic assessment of vulnerability to landslide:Application to the village of Lichtenstein, Baden-WURTTEMBETG,GERMANY[J].Engineering Geology,2008,101(1/2):33-48.
[8]UZIELLIM.Risk and vulnerability for geohazards—probabilistic estimation of regional vu lnerability to landslides[R].ICG Report,2006-2-7,Oslo.
[9]何思明,吴永,沈均.泥石流大块石冲击力的简化计算[J].自然灾害学报,2009,18(5):52-56.
He SI-MING,WU YONG,SHEN JUN.Simp lified calculation of impact force of massive stone in debris [J].Journal of Natural Disasters.2009,18(5):52-56.
[10]中国建筑科学研究院.JGJ3-2002#高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2002.
[11]潘家铮,建筑物的抗滑稳定和滑坡分析[M].北京:水利出版社,1984:120.
[12]LOWBK.Reliability analysis of rock slopes involving correlated nonnormals[J].International Journal of Rock Mechanics and Mining Sciences,2007,44:922-935
[13]RAMLY H EI,MORGENSTERN N R,CRUDEN D. M.Lodalen slide:a probabilistic assessment[J].Can. Geotech.J,2006,43:956-968.
[14]秦荣.大型复杂结构体系可靠度[M].北京:科学出版社,2009:194-195.
[15]刘晶波,刘阳冰,闫实秋,等,基于性能的方钢管混凝土框架结构地震易损性分析[J].土木工程学报,2010,(2):39-47
LIU JING-BO,LIU YANG-BING,YAN QIU-SH I,et al.Performance-based seism ic fragility analysis of CFST frame structures[J].China Civil Engineering Jourual,2010,(2):39-47.
(编辑 胡 玲)
A Calculation Methed for Failure Probability of Typical Element at Landslide Risk
WUYue1,LIUDong-sheng2,LUXin,SONGQiang-hui
(1.Department of civil Engineering,Logistical Engineering University of PLA,Chongqing 400041,China; 2.Chongqing Bureau ofGeology and Minerals Exploration,Chongqing 400039,China)
From the point of view of system theory,the landslide hazard system includes two subsystem s:subsystem of hazard and subsystem of stricken.The consequence of landslide hazard is based on the interaction of these two subsystem s.previous studies concenerate on evaluation of landslide stability. Hence,the study of a typical element at landslide risk is focused.And a m ethod to calculate failure p robability of typical element(frame structure)at landslide risk is discussed.Furthermore,the influences of both impact force and impact resistance-capability of element at risk on failure probability are analyzed, which show s that,for each elements at risk,the landslide im pact area can be divided into absolutely dangerous zone,relatively dangerous zone and absolutely safety zone.In addition,w ith the condition that the structure failure probability is above 50%,as the variability of impact force increases,the structure failure p robability decreases;w ith the condition that structure failure p robability is below 50%,as the variability of impact force increases,the structure failure probability also increases.
book=46,ebook=15
Landslide;element at risk;Structure reliability.
TU457
A
1674-4764(2011)02-0045-06
2010-11-18
中科院山地灾害与地表过程重点实验室2008年度开放基金、成都理工大学地质灾害防治与地质环境保护国家重点实验室开放基金(GZ2007-04);科技导报社博士生创新研究资助基金(k jdb20090101-3);后勤工程学院研究生创新基金资助项目(LEU2007-01)
吴越(1981-),男,博士生,主要从事地质灾害风险评估与风险管理研究方面研究,(E-mail)w uyue_linyi@ 163.com
book=50,ebook=19

