软土盾构隧道开挖面支护压力极限上限解
吕玺琳,王浩然
(同济大学a.岩土及地下工程教育部重点实验室;b.地下建筑与工程系,上海 200092)
软土盾构隧道开挖面支护压力极限上限解
吕玺琳a,b,王浩然a,b
(同济大学a.岩土及地下工程教育部重点实验室;b.地下建筑与工程系,上海 200092)
考虑到天然软黏土非均质性和各向异性特点,采用极限分析上限法在不排水条件下对盾构隧道开挖面稳定进行了研究,推导了极限支护压力的计算公式。土体非均质性和各向异性对极限支护压力的影响有相互放大作用,在当土体非均质性和各向异性较强时,极限支护压力与隧道埋深的关系存在一个极大值。分析结果表明,在分析软土盾构隧道开挖面稳定性时,土体的非均质性和各向异性影响较大,不能忽略。
非均质;各向异性;软土;盾构隧道;支护压力;上限解
在盾构隧道施工中,施加合理的支护压力是保证开挖面稳定的关键,支护压力过小会引起开挖面土体坍塌,而过大又会导致土体隆起。早期对于开挖面稳定研究大多是建立在经验基础上的,如开挖面稳定系数法[1-2],极限平衡分析法[3-6]等。后来,理论基础更明确的极限分析理论也用于开挖面稳定分析,如Davis等[7]在不排水条件下,结合极限分析法得到开挖面稳定性系数的解。Leca和Dormieux[8]根据极限分析上下限理论得到了维持盾构隧道开挖面稳定的极限支护压力。吕玺琳等[9]对盾构隧道开挖面破坏模式和极限支护压力的主要影响因素进行了分析。近年来,为提高计算结果的准确性,一些学者提出了更精确的破坏模式进行极限分析,如Soubra[10]采用多块体破坏模式研究了开挖面坍塌与隆起破坏时的极限支护压力,Mollon等[11]在其基础上作了进一步改进,得到了更优的结果。
由于受天然沉积及加载等影响,天然软黏土大多具有非均质性和各向异性的特点。非均质性和各向异性将显著影响土体不排水抗剪强度[12-13],从而影响开挖面稳定[14]。目前有关盾构隧道开挖面稳定性极限分析的文献中,绝大多数将土体作为均质[7-11,13]处理,特别是对各向异性的探讨几乎没有涉及。笔者正是针对当前关于这方面研究的不足,在不排水条件下对开挖面稳定进行了研究,推导了维持开挖面稳定的极限支护压力的计算公式,并深入研究了土体非均质性和各向异性对极限支护压力的影响。
1 开挖面稳定极限上限分析
1.1 软黏土不排水抗剪强度
对于正常固结或弱超固结土,不排水抗剪强度随深度变化符合线性规律[13]:

式中:cz为深度z处土体的不排水抗剪强度;c0为地面土体的不排水抗剪强度;ρ为土体强度随深度的变化率。如图1(a)所示。

图1 土体不排水抗剪强度变化规律
土体在任一方向的不排水抗剪强度为:
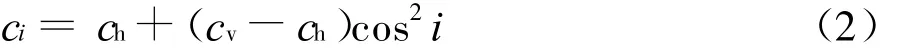
式中:ci为主应力与竖直方向夹角为i时土体的不排水抗剪强度;ch和cv分别为水平和竖直方向土体不排水抗剪强度。如图1(b)所示。
令各向异性系数k为:

若土体为各向同性的,则有k=1.0。
将式(3)代入式(2),得:

联立式(1)和(4)可得:

1.2 极限上限分析
接下来利用极限分析上限法对盾构隧道开挖面稳定性进行分析。极限分析上限法根据构造的运动许可速度场,通过使得外力作的功率与内部耗损功率相等来得到问题的上限解。虽然对同一问题可以构建无数个运动许可速度场(破坏模式),且每个运动许可速度场都可以得到一个相应的上限解,但所选的破坏模式越接近实际情况,所得结果就越接近真解。根据吕玺琳等[9]参照 Terzaghi[15]关于地基承载力计算而提出的破坏模式,通过令φ=0分析不排水状态,假定开挖面的破坏模式由2个刚性块体I、III和一个剪切区II构成,如图2所示。块体I为一矩形O′OBB′,其底边为线OB,高为上覆土层厚度C;块体III为一等腰直角三角形OAA′,AA′线与水平方向夹角为π/4;剪切区II为一圆弧A′B围成的剪切区OA′B,点O为圆心,点B和点E分别为圆弧的起点和终点,根据几何关系有OB=OA′=AA′=r0。且有:

根据速度相容关系,可得vI=vII=vIII。

图2 不排水条件下极限分析上限法采用的破坏模式
块体I重力所做的功率为:

扇形剪切区II内微元土体重力做的功率为:

积分式(8),可得剪切区II重力所做的功率为:


将式(7)及(9)-(14)和(16)代入式(17),即可得到支护压力的表达式。并将支护压力表示为:


2 非均质和各向异性对极限支护压力的影响
在不排水条件下,根据上一节所建立的极限上限分析模型对非均质各向异性软土盾构隧道开挖面稳定进行研究。计算中隧道直径为10m,地表土体不排水抗剪强度为2 kPa,土体重度为17 kN/m3,无地表超载。计算得到的极限支护压力与非均质系数ρ的关系如图3所示,极限压力随非均质系数增大而线性减小,且当各向异性系数越大时,线性减小得越快。极限支护压力与各向异性系数k的关系如图4所示,极限压力随各向异性系数的增大而线性减小,且当非均质系数越大时,线性减小得越快。这表明土体非均质性与各向异性2种特性间具有互相放大作用。

图3 非均质系数ρ值对极限支护压力的影响
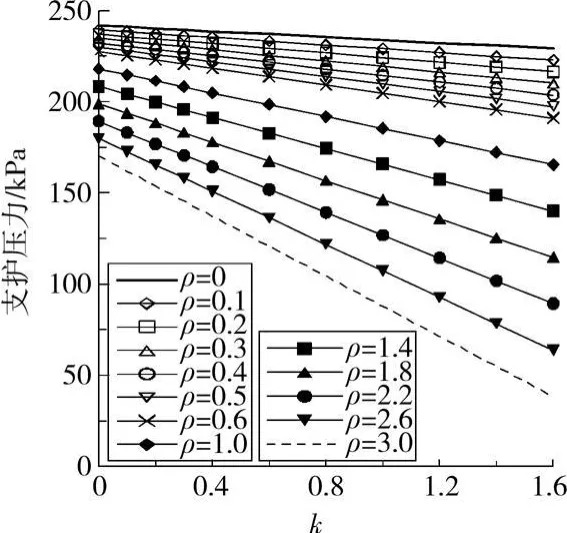
图4 各向异性系数k值对极限支护压力的影响

图5 隧道埋深比C/D值对极限支护压力的影响
隧道埋深对支护压力的影响如图5所示,当k值或ρ值较小时,支护压力随着隧道埋深比(C/D)增加而增大,且近似呈线性关系;但当k值和ρ值较大时,极限支护压力先随C/D值增加而增大,当C/D达到一定值时达到最大值,此后极限支护压力随C/D的增加而减小。经分析表明,这是由于随着埋深增加,土体自重对支护压力的影响逐渐小于土体抗剪强度对支护压力的影响引起的。
3 结 语
通过极限分析上限法对非均质各向异性黏土盾构隧道开挖面稳定进行了研究,推导了维持开挖面稳定极限支护压力的具体计算公式。结果表明:
1)极限支护压力随非均质系数ρ和各向异性系数k增大而线性减小,但随ρ的变化幅度更大。土体非均质和各向异性间具有互相放大作用。
2)当非均质性和各向异性较弱时,支护压力随隧道埋深增加而线性增大。当土体非均质性和各向异性较强时,支护压力在随隧道埋深达到一定值时达到最大值,此后随隧道埋深增加反而减小。
[1]BROMSB B,BENNERMARK H.Stability of clay at vertical openings[J].Journal of the Soil Mechanics and Foundations Division,ASCE,1967,96(1):71-94.
[2]韦良文,张庆贺,邓忠义.大型泥水盾构隧道开挖面稳定机理与应用研究[J].地下空间与工程学报,2007,3 (1):87-91.
WEILIANG-WEN,ZHANG QING-HE,DENG ZHONGYI.Research on mechanism and application of face stability in large slurry shield tunneling[J].Chinese Journal of Underground Spaceand Engineering,2007,3(1):87-91.
[3]XILIN LU,MAOSONG HUANG,HAORAN WANG. Face stability analysis of plane strain tunnel in limit theorem[C]//In:Recent Developments of Geotechnical Engineering,2010:188-193.
[4]LI Y,EMERIAULT F,KASTNER R,ZHANG Z X. Stability analysis of large slurry shield-driven tunnel in soft clay[J].Tunnelling and Underground Space Techno logy,2009,24 472-481.
[5]JANCSECZ S,STEINERW.Face support for a large m ix-shield in heterogeneous ground conditions[C]// Tunneling,1994,94:531-550.
[6]ANAGNOSTOU G,KOVARI K.Face stability conditions with earth-p ressure-ba lanced shields[J]. Tunneling and Underground Apace Technology,1996, 11(2):165-173.
[7]DAV IS E H,GUNN MJ,MAIR R J,et al.The stability of shallow tunnels and underground openings in cohesive soil[J].Géotechnique,1980,30:397-416.
[8]LECA E,DORMIEUS L.Upperand lowerbound solutions for the face stability of shallow circular tunnels in frictional material[J].Géotechnique,1990,40:581-606.
[9]吕玺琳,王浩然,黄茂松.盾构隧道开挖面稳定极限理论分析[J].岩土工程学报,2011,33(1):57-62.
LU XI-LIN,WANG HAO-RAN,HUNAG MAOSONG.Study on the face stability of shield tunnel in limit theory[J].Chinese Journal of Geotechnical Engineering,2011,33(1):57-62.
[10] SOUBRA A H.Three-dimensional face stability analysis of shallow circular tunnel[C]//International Conferenceon Geotechnical and Geological Engineering, 2000,Australia:Melbourne.
[11]MOLLON G,DIAS D,SOUBRA A H.Face stability analysis of circular tunnels d riven by a pressurized shield [J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2010,136(1):215-229.
[12]AUGARDE C E,LYAMIN A V,SLOAN S W. Stability of undrained p lane strain heading revisited[J]. Computers and Geotechnics,2003,30:419-430.
[13]MOSLEH A.Upper-bound so lutions for bearing capacity of strip footings over anisotropic nonhomogeneous clays [J].Soils and Foundations,2005,45:109-124.
[14]周维祥,黄茂松,吕玺琳.非均质黏土地基中平面应变隧道最小支护压力数值模拟[J].岩土力学,2010,31 (S2):418-421.
ZHOU WEI-XIANG,HUANG MAO-SONG,LǜXILIN.Numerical simu lation ofm inimal support p ressure of plane strain tunnel in non-homogeneous clay[J], Chinese Journalof Rock and Soil Mechanics,2010,31 (S2):418-421.
[15]CHENW F.Lim it analysis and soil p lasticity[M].New York:Elsevier Scientific Publishing Company,1975.
(编辑 王秀玲)
Upper Bound Solution of the Lim it Support Pressure during Shield Tunneling in Soft Clay
LǜXi-lina,b,WANGHao-rana,b
(a.Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education,
b.Department ofGeotechnical Engineering,Tongji University,Shanghai 200092,P.R.China)
Considering the nonhomogeneity and anisotropy of the undrained shear strength of soft clay,the face stability of shield tunnelwas studied by upper-bound lim it analysis,and the formula for calculating the limit support p ressure was obtained.The influences of nonhomogeneity and anisotropy on the limit support pressure amp lify w ith each other.The relationship between limit support pressure and tunnel depth also depends on the nonhomogeneity and anisotropy;the limit support p ressure reaches m aximum value at a certain tunnel depth when nonhom ogeneity and anisotropy are strong enough.These results show the nonhomogeneity and anisotropy of clays cannot be neglected when analyzing the stability of tunnel face.
nonhomogeneity;anisotropy;soft clay;shield tunnel;support p ressure;upper-bound solution
TU921
A
1674-4764(2011)02-0065-05
2010-07-24
国家自然科学基金青年科学基金(50908171);上海市晨光计划(10CG23);同济大学青年优秀人才培养行动计划(2009KJ097)
吕玺琳(1981-),男,博士,主要从事岩土力学与工程方面研究,(E-mail)xilinlu@tongji.edu.cn。

