煤矿环境下无线传感器定位技术的算法研究

何维斌

现在，我国大部分煤矿安全系统的传感器基本上都是采用有线方式架构，但这些传统的监测方法和思路存在许多不足，相当程度上影响了正常检测井下信息以及矿难的搜救展开，因此，开发无线传感器网络监控系统非常紧迫。

1 无线传感器网络的定位机制

在无线传感器网络系统中，常常把定位机制划分为：基于距离的定位机制和基于非测距的定位机制。在基于距离的定位机制中，根据测量节点间距离或方位，可采用的方法有接受信号强度指示器 RSSI［1］(Received Signal Strength Indicator)，到达时间 TOA(Time Of Arrival)，到达时间差 TDOA［2］(Time Difference On Arrival)，到达角 AOA［3］(Angle Of Arrival)等。基于TOA的定位精度高，但要求节点间保持精确的时间同步;RSSI是随着实际情况变化而变得很不稳定的方法;TDOA方法受限于超声波传播距离有限和非视距传输问题对超声波信号传播的影响;AOA也受外界环境影响，而且需要额外硬件。因此，本文主要基于非测距定位算法来进行分析。

2 基于非测距的典型定位算法

2.1 APIT 定位算法［4］

APIT定位算法的基本思想为：首先未知节点选择3个信标节点，要求是这3个节点是能够与未知节点互通信息的，然后检测此未知节点是在所选3个节点组成的三角形内部还是外部;然后再选择其它不同的3个信标节点做同样的检测;如此穷尽检测，直到取得所需的精度值，假如未知节点在所得三角形内部，就把此三角形质心坐标作为未知节点的位置坐标。

APIT算法的特点：由于采用的是穷尽检测，因此，误差概率比较小，但是此算法要求较大密度的信标节点，因此较为复杂。

2.2 DV －Hop 定位算法［5］

DV－Hop定位算法采用的是网络中的距离向量路由算法的基本思想。其原理是：首先计算出未知节点与信标节点的最小跳数，然后估算平均每跳的距离，进而让最小跳数乘以平均每跳距离，这样就可得未知节点与信标节点之间的距离，最后采用极大似然估计法的思想可得未知节点的坐标。

2.3 Amorphous定位算法［6］

Amorphous定位算法的使用需要满足两个条件，分别为：全部的信标节点和未知节点有效通信半径基本相同而且是已知值、无线传感器网络设置区内节点密度相当大或网络连通性较优。它是利用最大似然估计法的思想得到未知节点坐标。

2.4 质心定位算法［7］

质心定位算法的基本思想为：利用了找多边形的质心思想，首先是确定某一范围，然后让信标节点规律性的给邻近节点发送广播信息分组，当未知节点收到各个信标节点信息分组信号值大于门限值时，就可以通过节点坐标公式得出此未知节点的坐标。质心定位算法具有许多优点，例如，信标节点的数目固定，而且它们传送信号范围也是相互叠合的，这样就不再需要信标节点和未知节点之间去协调，质心算法实现起来相当简单，而且精确度较高。

3 两种环境四种算法定位性能的仿真分析

3.1 煤矿通道环境下定位性能分析

狭长的煤矿通道环境下，由于受实际情况限制，仿真环境设定如下：传感器节点分布区域为二维平面［0，100］×［0，5］m2，将信标节点错位分布于该区域的左右两边，未知节点随机分布在该区域，信标节点总数(AQ)为20个;未知节点总数(NQ)100个;通信半径(DC)50 m。由Matlab随机生成100个点(作为未知节点)分布在的仿真区域内，20个信标节点，完成的WSN节点分布见图1。

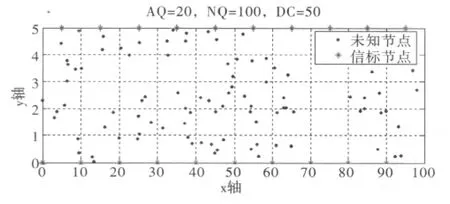
图1 WSN节点分布示意图

煤矿通道环境狭长而结构复杂，在这样环境下，对异常情况进行精确定位，需要从多方面进行考虑，来找出一种更适于这种环境的定位技术。因此，根据定位算法的性能影响因素，从以下方面来分析：

1)距离估算误差的影响。

DV－Hop和Amorphous算法是采用不同方法对节点间距离估算，定位受距离误差影响较大;APIT定位算法和质心定位算法无需知道此距离，因此，定位时基本上不受距离估算误差的影响。以下通过MATLAB仿真实验来分析距离估算误差对Amorphous定位算法、质心定位算法和APIT定位算法定位性能的影响。

选择对Amorphous定位算法、APIT定位算法、质心定位算法做1 000次MATLAB仿真，可以得到比较真实的结论，下面给出通信半径(DC)为50 m，信标节点为10，以上算法距离估算误差对平均定位误差影响的仿真结果，见图2。

图2 距离估算误差对定位性能的影响仿真

由图2可知：距离估算误差对APIT算法和质心算法的定位误差影响相当小，但对Amorphous定位算法的影响较大。可得出结论：当要求定位精度较高时，不宜采用Amorphous定位算法。

2)信标节点密度的影响。

在WSN定位系统中，锚节点(即信标节点)与普通终端节点相比较，硬件成本明显较高，但是大量地设置信标节点却能显著的减少定位误差;为了提高定位精度，常常会增加锚节点，这样一来，系统成本相应地提高。因此，锚节点布设的多少也会影响系统定位的性能。下面是以信标节点密度作为因素来参考，给出锚节点密度的计算公式：

式中：

DA—锚节点密度;

AQ—锚节点的数量;

NQ—未知节点的数量。

根据质心算法和APIT算法理论，质心算法是求解多边形的质心来估计真实未知节点的坐标;而APIT算法求解多个三角形共交区域的质心来估计未知节点的坐标，见图3。

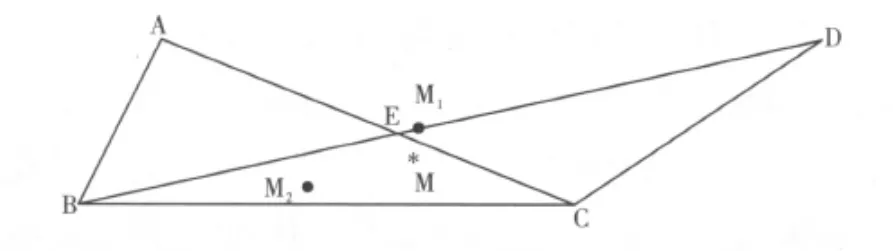
图3 质心估计和APIT估计坐标同真实坐标的位置比较

在未知节点M周围有A、B、C、D四个信标节点，由质心算法可得到四边形ABCD的质心为M1;而根据APIT算法原理，可找到未知节点M在△ABC和△BCD的共交区域△BEC中，再求解出△BEC的质心M2。此时，明显可以看出M2比M1到真实坐标M的误差要大的多。因此，可以得出APIT需要在信标节点密集的情况下，尽可能的减小共交区域，而且需信标节点分布均匀，才能达到好的定位性能。下面通过仿真来验证上面的结论。

仿真条件同上所设狭长的通道环境。信标节点数目有 5 种情况：6、10、16、20、30 个信标，未知节点总数为100(NQ=100)。为了得到较为真实的结论，对APIT定位算法和质心定位算法随机做1 000次MATLAB仿真，去除APIT失效情况，得到平均定位误差。算法仿真结果见图4。

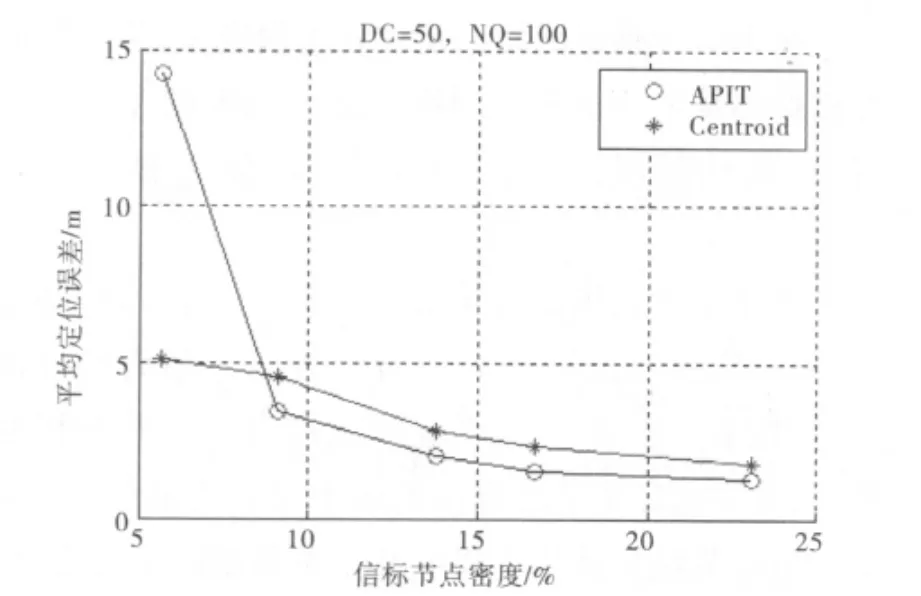
图4 信标节点密度对定位性能影响的仿真

从仿真图中可以看出，APIT算法比质心定位算法受信标节点密度影响大，因此，APIT算法在信标节点不密集的情况下，定位误差明显增大。实际应用中，常常需要在信标节点不密集的情况下解决定位问题，如发生矿难。质心定位算法的定位误差受信标节点密度影响较小，所以，质心定位算法比APIT算法更具有实际应用价值。

根据以上的分析和仿真验证，证实了在煤矿通道环境下进行定位，质心算法比其他三种算法都有效。

3.2 煤矿井下密集型环境下定位性能分析

在煤矿井下密集型环境中，由于定位范围较大，未知节点密度高，信标节点少，因此环境设置如下：［0，100］×［0，100］m2的二维区域，锚节点(即信标节点)在该区域是均匀分布的，未知节点在该区域是随机分布的，锚节点总数(即信标节点总数)为12个(即AQ=12)，未知节点总数为200个(NQ=200)，完成后的WSN节点分布，见图5所示。

在井下密集型节点环境下，由于特殊情况使信标节点数减少，如何还能够利用剩余的信标节点进行有效的定位，这就需要找出一种定位技术可以在这种情况下有较好的定位性能。针对几种典型算法做以下分析。

1)定位覆盖率的分析。

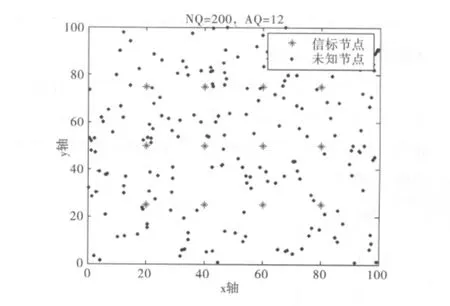
图5 传感器网络节点分布示意图(100 m×100 m)

根据APIT算法特性，该算法虽然误差概率相对较小，然而因定位区域需要细分和未知节点与参考节点必须为相邻的需求，为此，该算法对参考节点密度要求相对较高。因此，在较少信标节点情况下一般定位效果不好。下面通过仿真实验，分析信标节点密度对APIT、质心算法、DV－hop算法定位覆盖率的影响情况。

仿真环境如上所设，信标节点数目有5种情况：12、20、30、42、56，假设未知节点总数为200 个(即 NQ=200)，通信半径为30 m。一共做1 000次MATLAB仿真，这样可得知此算法失效的总数量，计算定位覆盖率。仿真分析见图6。

图6 三种算法定位覆盖率比较示意图

从图6可以看出，当信标节点密度不够时，在煤矿井下密集型环境下APIT算法的定位覆盖率不到30%。定位的盲区较大，明显不能满足定位的要求，因此，APIT不适用于应用在此环境下进行定位。

2)信标节点密度对定位精度影响。

根据DV－hop算法原理，此算法需要计算平均每跳的距离和未知节点与信标节点的最小跳数，然后利用最小跳数乘以平均每跳距离，这样能得到未知节点与信标节点之间的距离，再利用最大似然估计法的思想可得到未知节点的坐标。因此，这种算法能够根据有限的几个信标节点，计算最小跳数和平均每跳距离来求解未知节点坐标。需要的信标节点较少，是一个可扩展的算法，对于各向同性的密集网络，也能够达到适当的定位精度。

为了验证以上的分析结论，下面在不同信标节点密度下，来对DV－hop和质心算法的定位性能进行分析。仿真环境设置同上节。1 000次仿真结果求平均值，见图7。

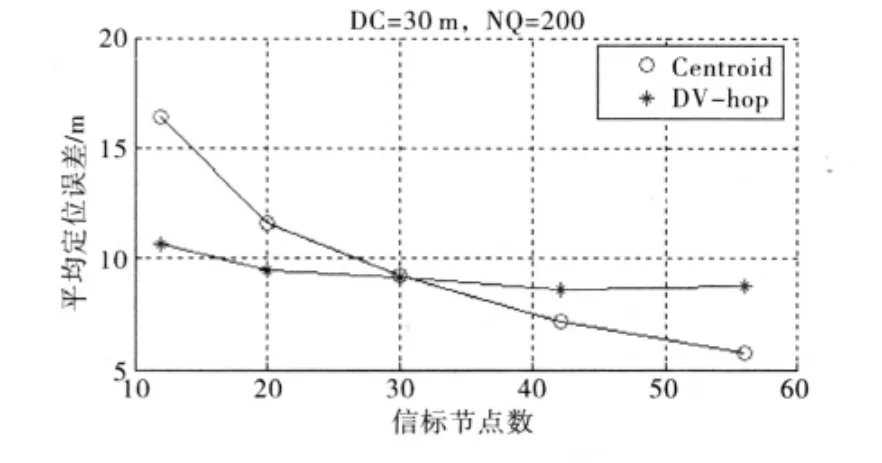
图7 信标节点密度不同时两种算法定位性能比较

从图7可看出，DV－hop算法定位性能受信标节点密度影响不大，在信标节点为12的很少情况时，也能够对200个未知节点进行较好的定位，误差在10 m左右。而质心算法尽管在信标节点为56时，定位误差只有5.7 m;但信标节点为12和20的较少情况下，定位误差高达16 m。

因此，从以上分析可以证实DV－hop算法更适用于煤矿井下密集型环境，信标节点较少的情况。

4 结论

在无线传感器网络的定位技术研究中，最重要的性能指标是定位误差。而影响定位误差的主要因素有：距离估算误差、信标节点密度、定位覆盖率等方面。

本文主要在煤矿通道和煤矿井下平台两种环境下，对定位算法进行研究。通过对以上距离估算误差、信标节点密度、定位覆盖率这些方面进行分析并仿真，分别验证了质心算法最适于煤矿通道环境，而DV－hop算法则适用于煤矿井下密集型网络的定位。可为实际应用中，根据不同环境选择相适合的定位技术提供一定的参考。

［1］ 马祖长，孙怡宁.无线传感器网络节点的定位算法［J］.计算机工程，2004，30(7)：13－14.

［2］ 孙利民，李建中.无线传感器网络［M］.北京：清华大学出版社，2005：3－25.

［3］ Doherty L，Pister K，and Ghaoui L.Convex position estimation in wireless sensor networks.Proc.of the IEEE INFOCOM［M］.Anchorage，AK，USA，2001：1655 －1663.

［4］ 杨 维，李 澎，孙继平.类矩形矿井巷道中UHF宽带电磁波统计信道建模［J］.煤炭学报，2008，33(4)：467－472.

［5］ 史 龙，王福豹.无线传感器网络自身定位算法研究［D］.西安：西北工业大学硕士论文，2006.

［6］ Priyantha N B，Balakrishnam H.Anchor－ Free Distributed Localization in Sensor Networks［M］.MIT Lab for Computer Science，2003.

［7］ Nagpal R，Shrobe H.Bachrach J.Organizing a global coordinate system from local information on an ad hoc sensor network［A］.Zhao F，Guibas L.Proceedings of the 2nd International Workshop on Information Processing in Sensor Networks.Berlin，Germany：Springer－ Verlag，2003：333 －348.