关于ePSF模型的一个注记

朱丽莎，孟小华，张庆丰

（暨南大学 计算机科学系，广东 广州 510632）

有效点扩散函数ePSF(Effective Point-Spread Function)方法是由ANDERSON等[1]提出的用于测量哈勃空间望远镜HST(Hubble Space Telescope)星象的方法，该方法消除了长期困扰HST图像测量的相位误差效应，是一种有效而准确的方法，不仅可以广泛用于欠采样图像的测量,甚至也可以用于非欠采样图像的测量[2,3]。该方法用于欠采样星象的测量,首先必须建立图像的ePSF模型，然后再利用该ePSF模型测量图像中星象的位置。因此建立准确的ePSF模型是该方法的关键。

建立准确的ePSF模型的基本原理是对不够精确的大量的单个星体的PSF模型逐渐精化得出统一的单个图像的ePSF模型。虽然原则上选择的星体越多得到的PSF模型应该越准确，但实际上星体越多，计算量越大，这将耗费大量的资源和时间，在实时观测中，这是不能承受的。此外,采样星体越多带来的噪声也越多，未必能够得到很好的ePSF模型。反之,如果星体数目很小，ePSF模型则将失去准确性，那么选择多少星体来得到该图像的PSF模型就是一个需要讨论的问题。本文对采样星体的个数和ePSF模型的准确性关系进行了研究，指出了模型网格的细密度对准确性更重要，这对天文测量的实践具有指导意义。本文首先介绍ePSF模型的计算过程和算法,然后详细介绍所做的实验，最后给出了实验结论。

1 ePSF模型计算方法

ePSF算法的第一步是计算ePSF模型，第二步是由该模型拟合星体的光通量分布确定星体的位置。第二步的重点是PSF模型的计算，步骤如下：

(1)从星象图中选取高性噪比的恒星作为采样星体。

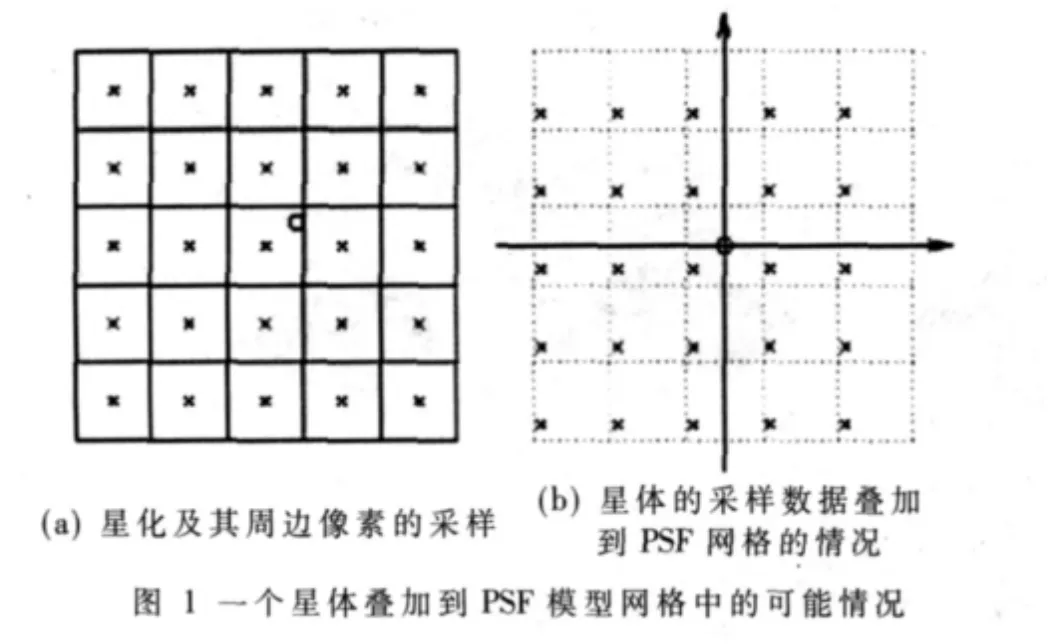
(2)获取采样星体中心周围m×m个像素的方形区域内的光通量分布(如图1所示)，每个星体的中心一般来说并不是整数的像素位置,所以，星体的中心相对于PSF模型的网格中心会有偏差，如图1(a)所示，星体的中心(图中的圆圈)并不一定落在图中像素的中心(图中的×)。

(3)将被采样星体的区域叠加到PSF网格区域(图1(b)显示了一个星体的采样区域叠加于PSF网格区域的情况)。在ePSF方法中一个图像的PSF模型是用离散的规则网格点处的值来表达的,也就是说,PSF模型是一个离散网格模型。该方法认为,星象中的每个星体及其周边的像素的灰度值是对PSF模型的一个采样，星象中有多少星体,则对该星象的PSF模型采样了多少次。

(4)当所有的采样星体及其周边像素值都叠加到PSF网格时，将得到如图2所示的情况(图中将PSF的网格进行了进一步的细分)，在每个PSF的细小网格内，将有许多星体采样值，按照3σ准则，剔除异常采样后再取平均，即可得到所有PSF细小网格上的灰度值，从而可以得到准确的实际PSF网格模型。

以上四步结束后，在实际处理中为保证PSF网格模型的光滑与对称，还将采用一些措施对其进行光滑和网格中心位置的微调[1]。

2 实验步骤

因为真实图像的有效点扩散函数是未知的，所以计算出来的点扩散模型无法比较。本实验采用人工图像进行计算比较，包括3个步骤：(1)设定人工图像的有效点扩散模型，按照该模型随机生成若干星体，形成一个天文图像；(2)用第二部分所述的方法对人工图像进行PSF模型计算；(3)将设定的有效点扩散模型与计算所得的PSF模型进行比较，计算模型误差。

2.1 人工图像的生成

要生成人工图像，首先要生成一个天空背景图像，然后在此基础上叠加许多星体。首先生成一个分辨率为2 024×2 024的图像,该图像设定天空背景灰度为 500，并叠加Poisson噪声，以模拟真实天空背景。然后在这个图像上叠加了2 500个具有随机位置的星体。这2 500个星体的像素位置服从一种特殊的position分布，整数部分是随机的，分数部分服从0～1的之间均匀分布，即所有星象的像素相位是均匀分布的。因为是人工生成的星象，所以可将每个星象的像素相位位置理想化，以利于PSF模型的计算，从而确保每网格内包含指定数量的采样星体数据。

根据KING[4]的研究,星象的大部分通量都被包含在一个核中,这个核的灰度分布近似于Gaussian分布，或者接近于高斯函数，如Moffat函数等，这就是所谓的PSF函数。这里对于模拟星体的PSF函数采样经典的二维高斯模型，即星体周围每个像素点处的光通量f和星体的中心位置之间满足二维高斯关系模型，对于模拟图像来说，就是星体周围的灰度分布满足如下关系：

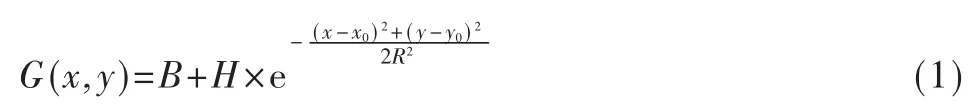
其中B代表背景;H代表高斯函数的峰值;R为高斯函数的标准差，它与视宁度有关(seeing≈2.355R);G(x,y)代表点(x,y)处的灰度值;(x0,y0)表示星体的中心位置。

实验中设定R=0.6369,即视宁度为1.5,因为ePSF方法是用于欠采样图像的一种有效方法,而视宁度为1.5的星象被认为是标准的欠采样图像。另外实验中H值在1 000～65 525之间随机取值,是为了保证每颗星体都有较好信噪比，可以作为有效采样星体。整体图像中每个星体还添加了Poisson噪声，这是在星象中最常见的噪声。最终生成的点扩散函数是已知的且像素相位均匀分布的星象图，以此作为实验的数据，所生成的图像局部如图3所示，整体与此相若。

2.2 进行ePSF模型计算时的影响因素

在ePSF方法中，ePSF模型也与网格的精细程度有关，假定单位像素划分为n×n个网格，n即标识了PSF网格的精细程度，实验中对不同精细程度的网格进行了考察，即分别考察了n取4,5,…,10等7种情况。计算出来的ePSF数值模型还与星体采样密度有关,用每网格内采样星体数据的数量k来标识采样密度。实验中对每一个 n值都考察了 k取 1,2，…，20等 20种情况，因为是人工生成星象，所以可以严格保证每网格内有要求数量的采样数据。

?

2.3 有效点扩散模型与所得PSF模型比较

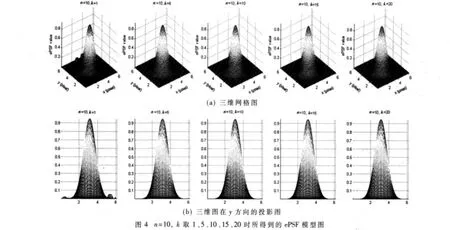
对 n、k不同取值总计 140种情况计算了 ePSF模型，并对这些模型数值进行了分析。图4所示为n=10时，将 k取值为 1、5、10、15、20时所得的 5个 ePSF模型图。其中图 4(a)是三维网格图，图4(b)是三维图在 y方向的投影图。

事实上每个PSF模型和准确Gauss模型都是有差别的，图 5显示了 n=10、k=5时所得 PSF模型和准确的Gauss模型的差别。图5是两者之差的三维网格图，可以看出其最大误差处在网格中心,其峰值很小不超过0.05。其他PSF模型和准确模型的差值图均与图5形状类似，当然其误差峰值不同，因此采用准确模型和计算的PSF模型之间的最大差值来衡量计算模型的误差。图4、图5大体反映了n=10时k取不同值所得的ePSF模型的情况及其误差情况。当n取其他值时也有类似的情况。

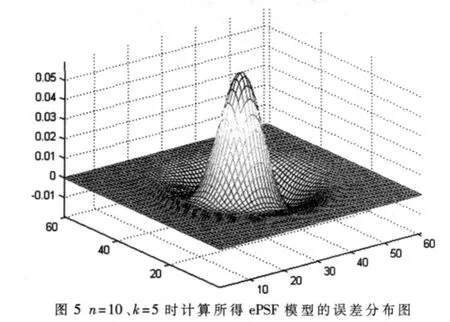
图6所示为 n、k取不同值时所得到 PSF模型的误差，表1是这些模型误差的数值表。

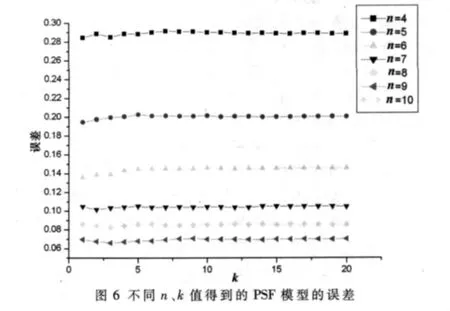
从图6可以看出，PSF模型的误差和网格的细密关系比较密切，网格越密，误差值越小，在网格固定的情况下，k取不同的值，模型误差变化不大。从表1的数据可以知道，对于固定的网格划分，k取不同值时，模型误差的绝对变化在0.01以内，相对变化在1%以内。理论上来说，k取值越大，相邻模型变化就越小，极限情况下，模型应该收敛到一个统一模型，这种极限模型称为稳定模型。一个网格划分对应一个稳定模型。从图6和表1可以看出，k取任何值，所得模型都很接近该网格划分对应的稳定模型，考虑到k取1时所得模型不够光滑，因此，认为k取2所得到模型很接近稳定模型。由此可以看出，在计算PSF模型时，网格的细密程度对计算模型的准确性影响很大，当网格划分固定后，只要保证每网格内有两个采样数据就可以得到稳定的模型。总体来说，采样星体数目达到2n2个就可以得到较好的稳定模型。

本文通过对模拟欠采样星象的处理实验，可知处理欠采样星象使用ePSF方法计算PSF模型时，每个网格的采样星体越多，计算结果越逼近一个稳定模型，这个稳定模型和真实模型的误差主要由网格划分的细密程度来决定，网格划分越密，模型误差越小。当网格划分固定时，每网格内有两个采样数据时即可得到一个较精确的稳定模型，即采样星体数目对ePSF网格模型的准确性影响不大。但在实际处理中，由于星体的相位差分布不均，因此平均每网格采样星体数目应该大于2。该结论在实际应用ePSF方法时,对更精确的建模有一定的指导意义。

[1]ANDERSON J,KING I R.Toward high-precision astrometry with WFPC2.I.Deriving an Accurate Point-Spread Function[J].PASP,2000,112:1360-1392.

[2]ANDERSON J,BEDIN L R,PIOTTO G,et al.Groundbased CCD astrometrywith wide field images I.Oberservations just a few years apart allow decontamination of field objects from members in two globular clusters[J].A&A,2006,454:1029-1045.

[3]张志渊,彭青玉.ePSF拟合法与Gaussian拟合法的比较[J].Astronomical Research&Technology,2010,7(2):132-139

[4]KING I R.The profile of a star image[J].PASP,1971,83:199-201.

[5]李展,彭青玉,韩国强.CCD图像数字定心算法的比较[J].天文学报,2009,50(3):340-348.