函数渐进界的性质研究

杨冀林

YANG Ji-lin

（赤峰学院 计算机科学与技术系，赤峰 024000）

1 函数渐进界的定义

定义1：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，如果存在自然数n0和正常数c，使得∀n≥n0，都有f（n）≤cg（n），则称g（n）是f（n）的一个渐进上界，记作f（n）=O（g（n））。

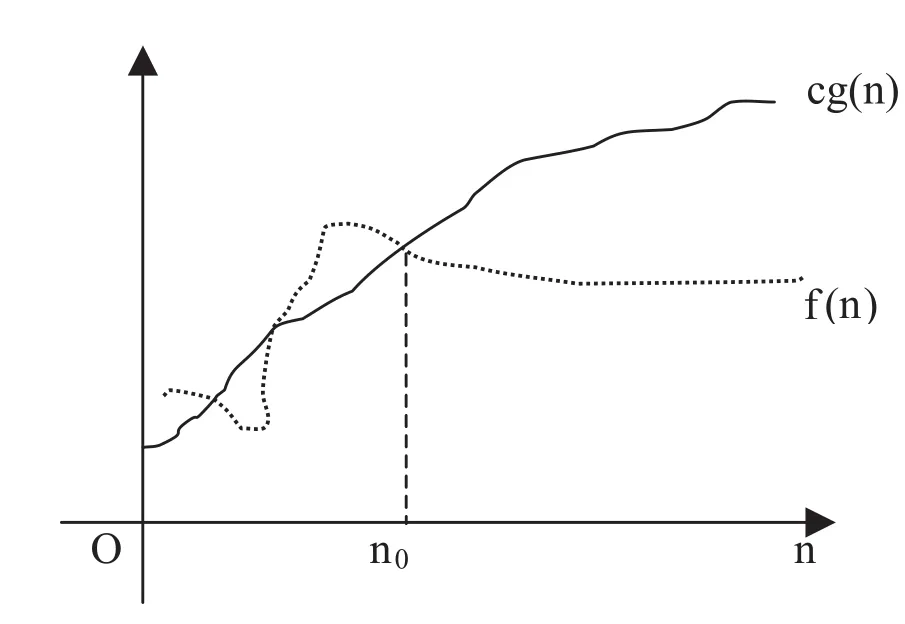
图1 渐近上界的几何解释

定义2：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，如果存在自然数n0和正常数c，使得∀n≥n0，都有f（n）≤cg（n），则称g（n）是f（n）的一个渐进下界，记作f（n）=O（g（n））。

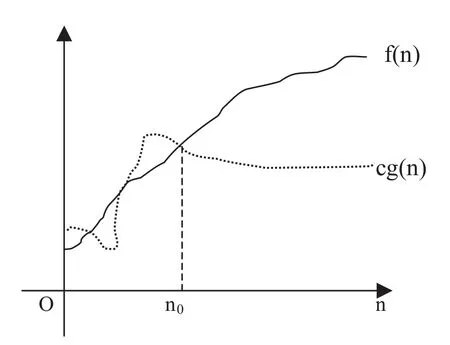
图2 渐近下界的几何解释

定义3：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，如果存在自然数n0和两个正常数c1，c2使得∀n≥n0，都有c1g（n）≤f（n）≤c2g（n），则称g（n）是f（n）的紧致的界，记作f（n）=Θ（g（n））。

由定义可知f（n）=Θ（g（n）），当且仅当g（n）= Θ（f（n））。

定义4：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，如果对每一个常数c＞0，都存在自然数n0，使得∀n≥n0，都有f（n）＜cg（n）则g（n）称是f（n）的一个上界，记作f（n）=o（g（n））。

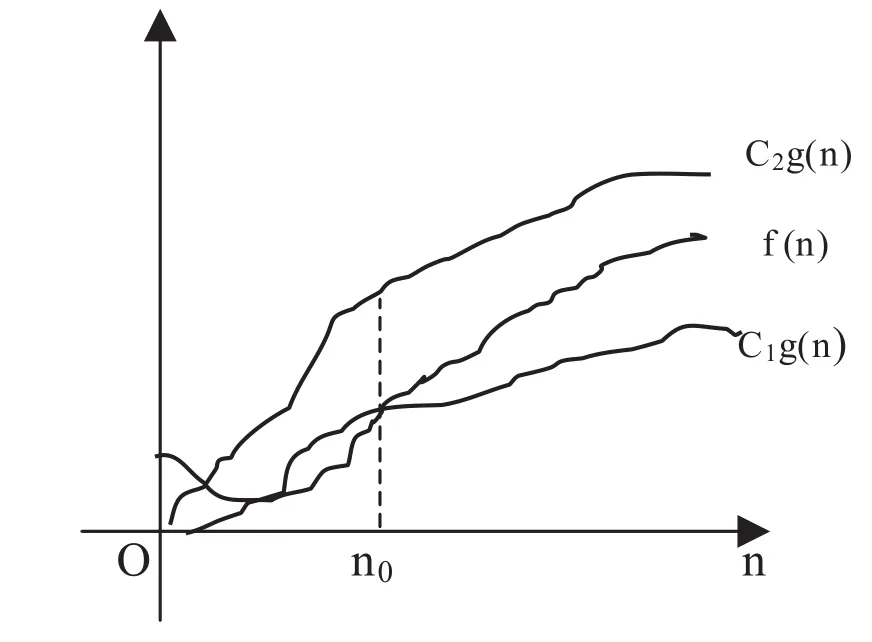
图3 紧致界的几何解释

2 函数渐进界的性质

定理1 f（n）=Θ（g（n）） iff f（n）=O（g（n））且f（n）=Ω（g（n））。

证明⇒，若f（n）=Θ（g（n）），则根据定义3，存在自然数n0和正常数c1和c2，

使得当n≥n0时有c1g（n）≤f（n）≤c2g（n）。

由上式右边不等式可得f（n）=O（g（n））

由上式左边不等式可得f（n）=Ω（g（n））

⇒，若f（n）=O（g（n））且f（n）=Ω（g（n））

根据定义1，存在自然数n1和正常数c1，当n≥n1，有f（n）≤c1g（n） （1）

根据定义2，存在自然数n2和正常数c2，当n≥n2，有f（n）≤c2g（n） （2）

取n0=max{n1，n2}当n≥n0时，由（1）（2）式有c1g（n）≤f（n）≤c2g（n）

所以有f（n）=Θ（g（n））。

定理2 符号Ο，Ω，Θ，ο具有传递性，即有以下等式成立：

1）若f（n）=O（g（n）），且g（n）=O（h（n）），则f（n）= O（h（n））

2）若f（n）=Ω（g（n）），且g（n）=Ω（h（n）），则f（n）= Ω（h（n））

3）若f（n）=Θ（g（n）），且g（n）=Θ（h（n）），则f（n）= Θ（h（n））

4）若f（n）=o（g（n）），且g（n）=o（h（n）），则f（n）= o（h（n））

以上四个结论的证明是类似的，现只证明结论1）

4.在年终考核时，考核政策应当向生活教师适度倾斜。原因在于，学校以教学为主，作为负责学生安全和后勤工作的生活教师往往会受到忽视，其工作上的辛勤付出往往无法得到与之匹配的重视和关照，影响其工作积极性。而通过适度的考核政策倾斜，能够让生活教师充满干劲，以更为饱满的工作热情投入到其本职工作之中。

证明1）若f（n）=O（g（n）），且g（n）=O（h（n）），则由定义1知，存在自然数n1和正常数c1，当n≥n1时，有f（n）≤ c1g（n），同时存在自然数n2和正常数c2，当n≥n2时，有g（n）≤c2h（n），取n0=max{n1，n2}，当n≥n0时，有f（n）≤c1g（n） ≤c1c2h（n）=c · h（n）（c=c1c2）

根据定义1有f（n）=O（h（n））。

定理3：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，则有以下结论：

于是，根据定义定义3有f（n）=Θ（h（n））。

定理4：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，若对于某个其它的非负实值函数h（n）有f（n）=O（h（n）），g（n）=O（h（n）），则有f（n）+g（n）=O（h（n））。

证明：由于f（n）=O（h（n）），所以存在自然数n1和正常数c1，当n≥n1时，有f（n）≤c1h（n）

同理由于g（n）=O（h（n）），所以存在自然数n2和正常数c2，当n≥n2时，有f（n）≤c2h（n）取n0=max{n1，n2}当n=n0时，由以上二式有：f（n）+g（n）≤（c1+c2）h（n）=c·h（n）（c=c1+c2），所以有f（n）+g（n）=O（h（n））。

则有f（n）+g（n）=Θ（f（n））。

定理5：设f（n），g（n）是定义在自然数集N上的两个非负实值函数，则有：

max{f（n），g（n）}=Θ（f（n）+g（n））。

证明：不妨假设max{f（n），g（n）} =f（n），于是g（n）≤f（n），所以 f（n）+g（n）≤2f（n）

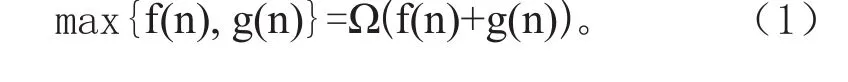
另一方面由于f（n），g（n）的非负性，显然有f（n）≤f（n）+ g（n）

从而有f（n）=O（f（n）+g（n）），即有

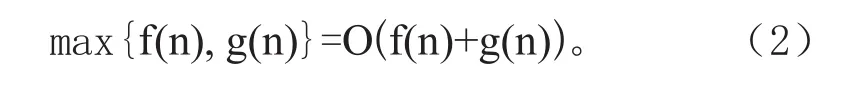
由（1）（2）式得到max{f（n），g（n）}=Θ（f（n）+g（n））。

1）若 ，则p（n）=O（nk）

2）若 ，则p（n）=Ω（nk）

3）若 ，则p（n）=Θ（nk）

结论1）2）的证明类似，仅证结论1）和3）。

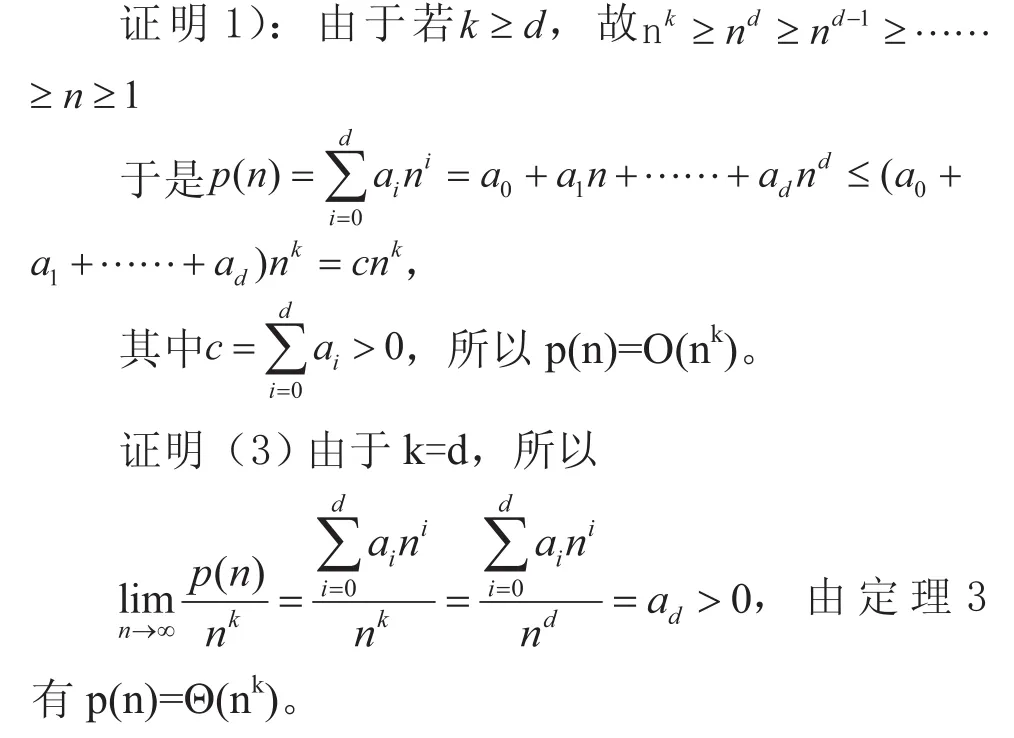
此外，函数渐进的界还有一些算法中常用的性质，限于篇幅列出不予证明：

1）任何常函数都是Ο（1），Ω（1），Θ（1）

2）Ο（cf）=Ο（f），Ω（cf）=Ω（f），Θ（cf）=Θ（f），其中是c正常数。

3）Ο（f ·g）=Ο（f）·Ο（g），Ω（f ·g）=Ω（f）·Ω（g），Θ（f ·g）=Θ（f）·Θ（g），

3 结论

函数渐进的界有许多重要性质，本文给出函数渐进界的概念及几何解释，Ο，Ω，Θ，ο符号及其等价性，分类归纳出算法分析中常用的一些性质，并利用极限理论给予严格的数学证明，这无疑将对系统掌握函数渐进界的性质，提高算法复杂度的分析能力提供有益的帮助。

[1]霍卫红,算法设计与分析[M].西安电子科技大学出版社，2005：8-11.

[2]Jon Kleiberg,Eva Tardos,算法设计[M].清华大学出版社,2007：25-30.

[3]M.H.Alsuwaiyel,算法设计技巧分析[M].电子工业出版社,2009：11-20.

[4]屈婉玲,算法分析与计算复杂性理论讲义,2010：27-31.

[5]卢开澄,计算机算法导论[M].清华大学出版社,1996：9-10.

[6]王晓东,计算机算法设计与分析[M].电子工业出版社，2004：1-5.

[7]宋文,杜亚军,算法设计与分析[M].重庆大学出版社：2004：5-7.