基于接触算法的气囊隔振特性分析及简化

张平豪，吴新跃

（海军工程大学 机械工程系，武汉 430033）

1 引 言

气囊隔振器主要由上下安装板之间囊式帘线橡胶层及囊内密封的高压空气组成，气囊隔振器的载荷可以通过充、放气来调整，通过高度保持装置，能够使各个气囊的高度保持一致,确保输出端与轴系的对中要求。另外，气囊隔振器还具有承载大（可达15t以上）、结构尺寸小、隔振频率低（一般小于2Hz）、阻尼性能好、无驻波效应和高频隔振性能好等优点，能够显著降低船舶的结构振动。

本文使用ABAQUS软件以及接触算法对两种安装模式不同的囊式空气弹簧隔振器的隔振特性进行了数值计算，在分析结果的基础上找出结构的薄弱之处，并提出相应的改进措施与有限元模型的简化方法。

2 求解方法理论分析

2.1 模态分析法

结构动力学问题有限元法的实质就是将一个弹性连续体的振动问题，离散为一个以有限节点位移为广义坐标的多自由度系统的振动问题。空间离散的多自由度时不变线性系统，其动力方程在无阻尼情况下可用二阶常微分方程表示：

式中：{x（ t ）}—位移向量；{ f（t ）}—激振力向量；[M ]—质量矩阵；[K]—刚度矩阵。

式中：ρ为材料密度；N为单元形函数，与有限元单元种类有关；B=LN，L为单元特征长度；D为弹性矩阵，由弹性模量和泊松比确定[1]。利用计算机强大的矩阵运算能力对离散动力学微分方程特征值问题进行求解是一条非常高效的途径。

2.2 接触算法

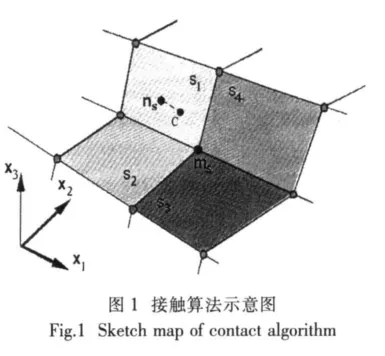
对称罚函数算法是ABAQUS处理接触-碰撞表面最常用的接触算法，其物理意义相当于在两个接触面之间放置一个法向弹簧，使得法向界面接触力的大小与穿透深度、主接触面刚度成正比。考虑两物体A、B接触问题，如图 1所示当前构形为 VA和VB，边界面为 ΩA和 ΩB，接触面记为 ΩC=ΩA∩ΩB，由于两物体不能互相重叠，事先无法确定两物体在哪一点接触，因此只能在每一时步，对比ΩC面上物体A、B的坐标或对比速率来实现位移协调条件。

式中N表示法线方向。

算法如图1所示，其有限元计算步骤如下：

（1）对接触面上的任一个从节点ns搜索与它最靠近的主节点ms。

（2）检查与主节点ms有关的所有主片Si，确定从节点ns在主片上可能接触点C的位置。

（3）检查从节点ns是否穿透主片，穿透则附加法向接触力fs，如有摩擦系数则计入摩擦力

由以上原理分析可知，接触算法能够解决梁单元模拟螺栓联结中节点相互进入的情况；而且接触单元没有质量，不会改变系统质量矩阵；而且接触的添加非常方便。下面将接触算法与共节点处理进行比较计算，以验证上述分析。

3 隔振器模型介绍

3.1 几何模型

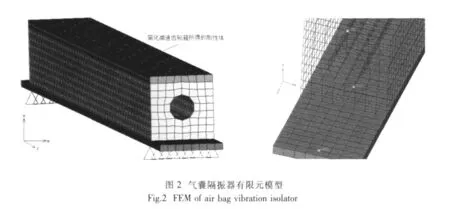
囊式空气弹簧隔振器模型如图2所示。气囊是由交叉的多层帘布（外层胶、帘布层、里层胶）组合而成的复合结构。气囊在隔振器中的安装方式为两种：一种是将气囊作为零件装配在隔振器中，另一种是将气囊硫化在隔振器中，利用橡胶的粘接性质将气囊和底座钢板做成一个整体。

3.2 有限元模型

从有限元的原理出发,模型几何形状越接近实物计算结果越准确，但是过分追求几何模型的细节，不但对计算结果精确度提高影响很小，而且会使得网格划分异常复杂，单元质量下降。所以本文采用CAD软件UG建立几何模型时,简化了一些圆孔、倒角等对计算结果影响较小的因素。

3.2.1 模型材料定义

隔振器除橡胶部件外都为钢材料。本文取钢密度为7 800 kg/m3,弹性模量为2.1×1011N/m2,泊松比0.3。橡胶材料的本构模型采用以连续介质力学为基础建立起来的唯象学理论模型

式中C10和C01为材料常数。根据参考文献[2]，在没有产生大变形情况下，可以使用准静态橡胶本构模型进行仿真。通过（6）式可以得到隔振器橡胶材料的材料参数：

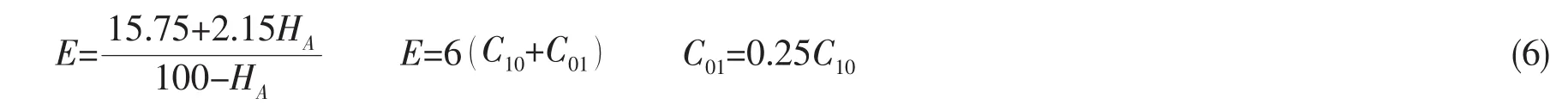
式中，E为弹性模量，HA为邵氏硬度。气囊橡胶采用某种氯丁橡胶，密度为1 230 kg/m3，邵氏硬度60，计算得 C10为 0.482 5，C01为 0.120 6。

3.2.2 单元选择

基于几何模型的隔振器有限元模型如图2所示，两个模型均由气囊、底座构成。气囊是由内外橡胶层、帘布层复合而成。内外橡胶层的厚度远小于气囊外型尺寸，可以选择壳单元模拟此结构。在ABAQUS/Standard中使用4节点四边形有限薄膜应变线性完全积分壳单元可以获得很高的精度，故内外橡胶层采用S4单元模拟。帘布层是橡胶气囊的承载骨架，考虑到几何非线性条件，使用ABAQUS/Standard提供的B22二次梁单元模拟。底座钢板由六面体网格划分，其单元类型为C3D20R。气囊用四面体壳单元划分，厚度5mm，共6 292个网格，6 292个节点。钢板用六面体单元划分，共1 280个网格，2 898个节点。本文讨论气囊的隔振特性，气囊上减速齿轮箱用刚体单元描述即可。在底座上施加简支约束，各个部件之间施加面—面接触用以保证作用力的传递[3]。

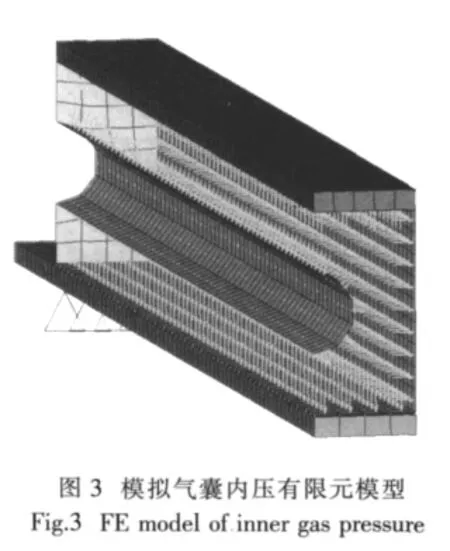
气囊内充满一定压力的空气，现有的有限元软件虽然已提供了描述空气的单元特性和材料模式，但它们也只是用于流体分析，不能描述密闭系统内的气体，所以本文并未使用气体单元，而是通过在气囊单元内表面施加法向压力来模拟。气囊内气体是密封的，其状态参数的变化满足气体状态方程；承载变形后气体在密闭容器中的体积发生了变化，即空气弹簧在变形后压力也会发生变化，因此施加压力载荷时不能直接加入一个恒定的压力载荷，文中采用增量法求解，在第一个载荷步求解完成后，计算出容器的体积，反求出此时的内压力，再将此压力加载于胶囊内壁，如此进行多步迭代可以较准确地模拟出内压的变化[4]。

4 有限元计算

气囊是囊式空气弹簧隔振器中最重要的隔振部件，它的性能好坏直接影响到隔振性能的好坏。气囊在隔振器中的安装方式为两种：一种是将气囊作为零件装配在隔振器中，另一种是将气囊硫化在隔振器中，利用橡胶的粘接性质将气囊和底座钢板做成一个整体。

在有限元分析中，两种不同气囊处理方法也需要不同的有限元处理方法。前一种方法需要用面-面接触算法处理气囊与底座钢板之间的界面；而后一种方法由于气囊和底座钢板是一个整体，两者之间不会产生相对滑动，因此其界面需要用共节点方法处理。为了分析两种处理方法对隔振效果的影响。本文分别用这两种方法处理圆柱隔振器，分别提取前20阶固有频率，然后施加相同的随频率变化的动态载荷进行分析。

4.1 固有频率提取

ABAQUS提供的基于模态的稳态动态分析（mode-based steady-state dynamic analysis）可以在指定频率内的谐波激励下，计算引起结构响应的振幅和相位，得到的结果是在频域上的。为得到结构的振型和固有频率需要设置频率提取分析步，ABAQUS/Standard提供了两种特征值提取方法：Lanczos方法和子空间迭代法（subspace iteration）[3]。前者适用于模型的规模较大，且需要提取多阶振型时。这里提取固有频率使用子空间迭代法，在于当提取的振型少于20阶时速度较快。下表为两种安装模式的前20阶固有频率：

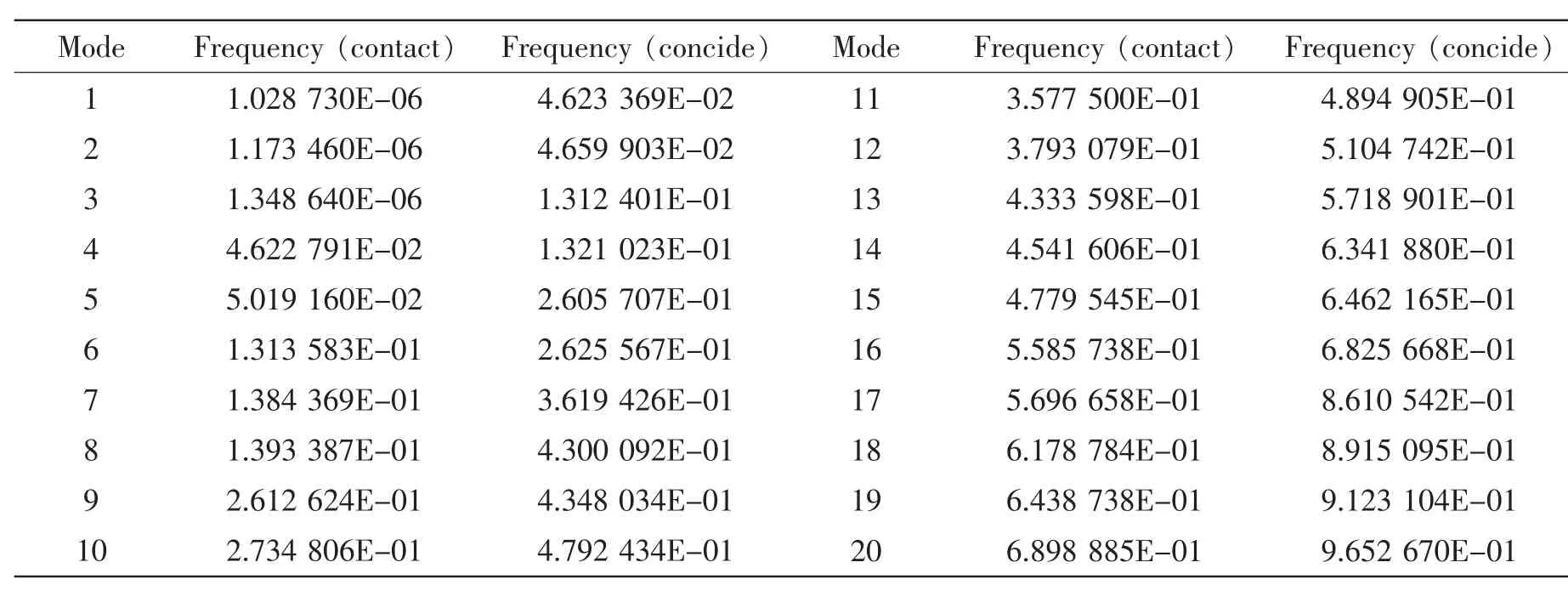
表1 前20阶固有频率Tab.1 The first 20th order intrinsic frequency

对比两种结果不难看出气囊隔振器隔振频率低，同时接触状态的固有频率比相应的共节点状态的低。分析其原因，是由于接触状态下橡胶气囊与钢板之间主要靠接触面切线方向的摩擦力产生相互作用，隔振器整体刚度较小；而共节点状态下橡胶气囊与钢板连成一个整体，隔振器整体刚度由于钢板较大的弹性模量而提高。

4.2 频率响应分析

基于上步提取的固有频率，在如图2所示简化成刚性体的减速齿轮箱上施加一个随频率变化的动态载荷，分析对比两种安装模式的频率响应。载荷的频率范围为0～10 Hz，幅值为1，提取响应的频率起始值为0.01 Hz，频率增量0.005 Hz，频率增量步200。响应点位置分布如图2右图所示，节点编号6695的1号响应点位于气囊顶端，节点编号为12517的2号响应点位于气囊和底板的界面上，节点编号为13565的3号响应点位于底板上。模型位于直角坐标系中，x坐标反映气囊宽度方向，y坐标反映气囊垂直方向，z坐标反映气囊长度方向。

（1）x方向激励时，3个响应点的幅频响应曲线如图4～7所示，上半部分为共节点处理的结果，下半部分为定义接触面的结果。1号响应点位于气囊顶端，设置接触面的幅值为共节点幅值的1/10；2号响应点位于气囊和底板的界面上，设置接触面的幅值为共节点幅值的1/2；3号响应点位于底板上，设置接触面的幅值为共节点幅值的2.3倍。分析其原因在于设置接触面比共节点的隔振器固有频率低、整体刚度也小得多，振动能量耗散较大。

（2）y方向激励时，2、3号响应点两种安装方式的响应结果趋于一致，结果区别在于1号响应点如图7所示，设置接触面的幅值为共节点幅值的1/2。分析其原因在于隔振器承受y向激励时，2、3号响应点在设置接触面时同共节点一样将接受来自垂直传向底板的激励；而1号响应点由于设置接触面的安装方式耗散振动能量较大，幅值较小。

（3）z方向激励时，两种安装方式的振动响应幅值较小，低于x、y向两个数量级，在这里不做过多讨论。

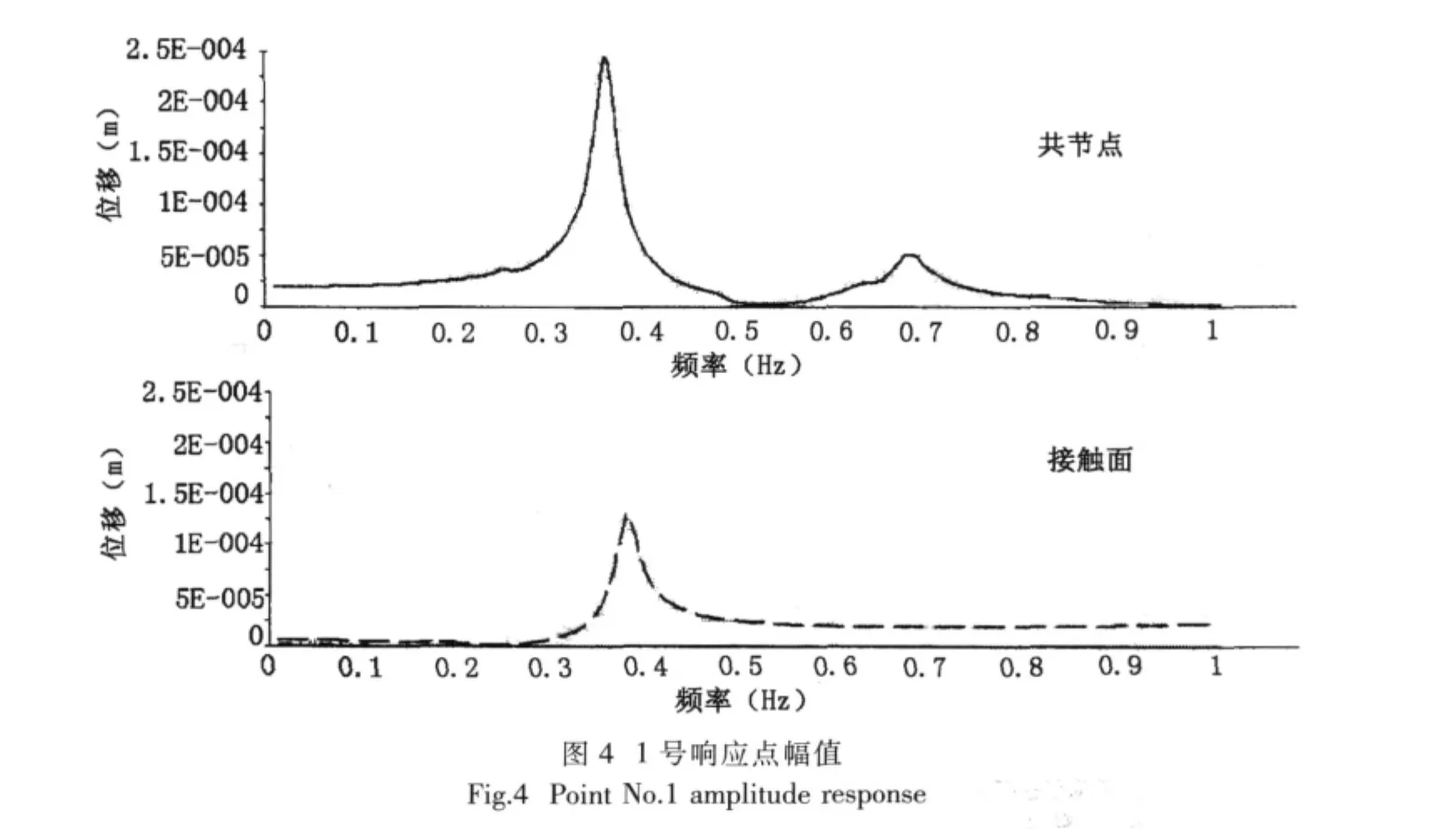
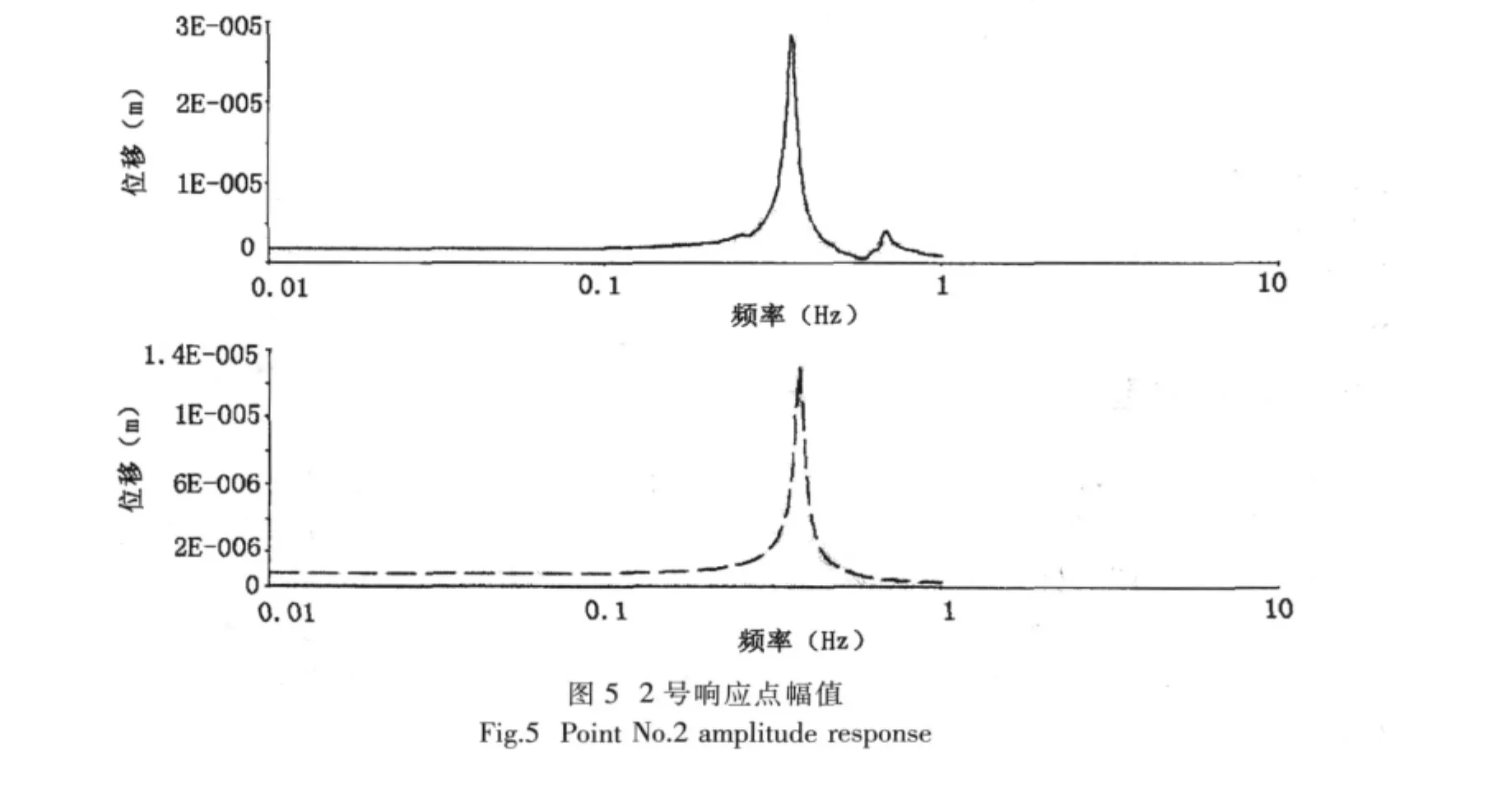
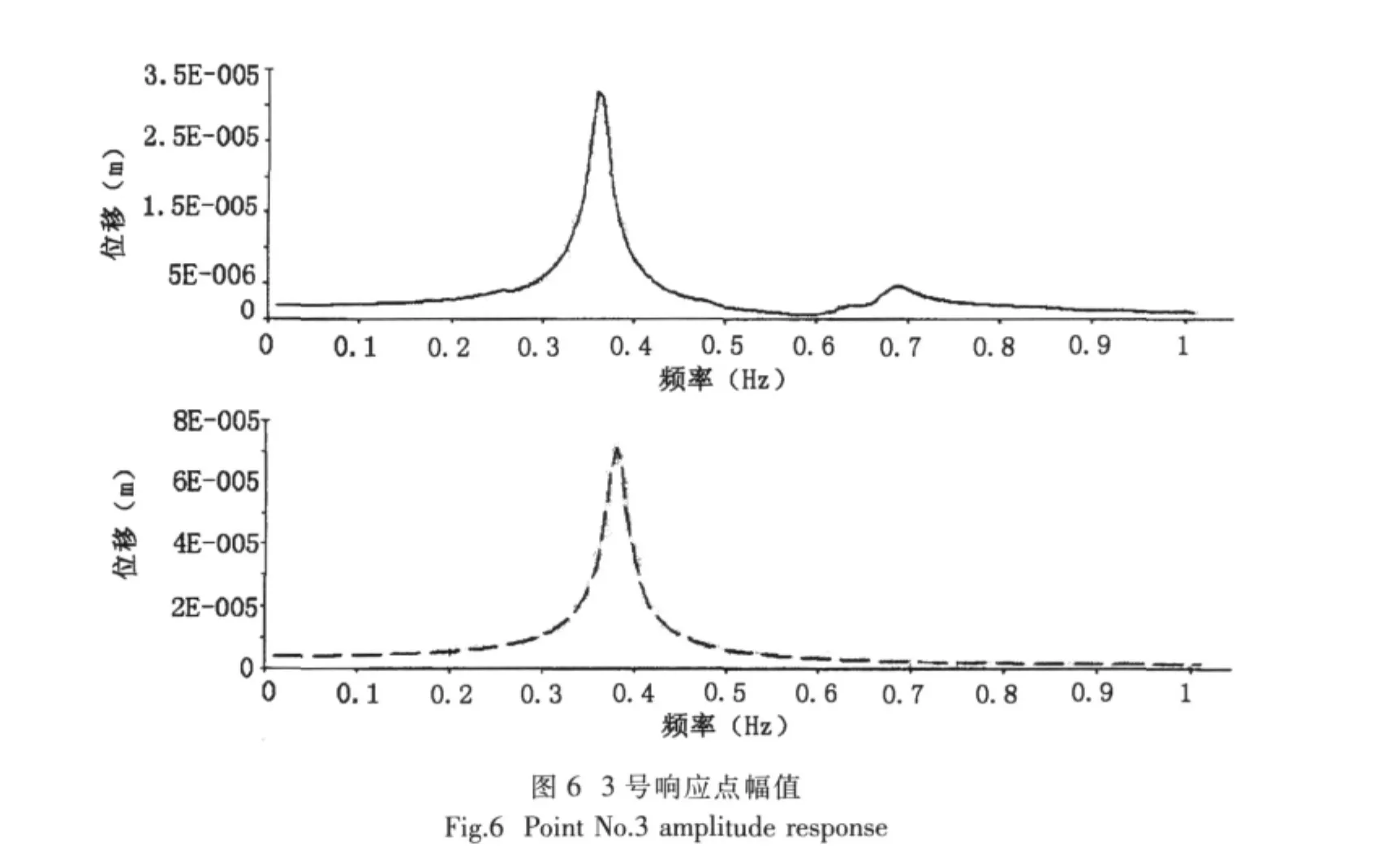
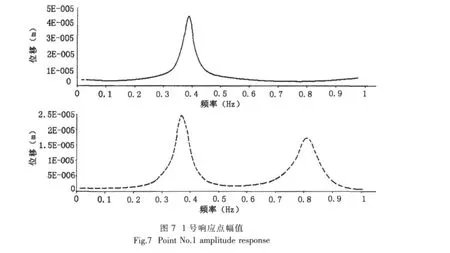
通过以上分析发现，设置接触面比共节点的隔振效果较好，也就是说将气囊作为部件安装在隔振器中，比将气囊硫化在隔振器中的隔振效果要好。但是装配存在安装对中扰动较大、设备联结的动态位移较大、设备位置固定不可靠等问题。两种隔振方式在使用中应灵活运用。

5 隔振器简化处理研究

囊式空气弹簧隔振器是船用设备隔振应用较广泛的一种隔振方式，因此囊式空气弹簧隔振器的有限元建模是设备系统级分析中必须解决的。最精确的有限元模型就是将隔振器各部件划分为较密的有限元网格，在施加弹塑性材料模型和各个接触面之间的接触单元上进行分析。但是这种方法太消耗计算机资源和人力劳动，一个普通的设备都含有多个隔振器，如果要都划分为精确的有限元网格，网格数量和计算时间都是天文数字。因此需要找到一种既容易划分网格，又不会降低计算精度的简化气囊模型来代替详细模型。

首先对两种隔振器在垂向载荷作用下的隔振器相对变形与载荷大小之间的关系进行了计算，图8为计算结果。从图中可以看出，气囊位移曲线具有明显的非线性。产生位移初期载荷梯度变化不大，即该区域刚度小；随着位移的逐渐加大载荷梯度也越来越大，表明气囊刚度变大。

根据上述研究结论，本文提出此类囊式空气弹簧隔振器的简化处理方法：由于隔振器主要隔振部件气囊的变形随载荷变化呈非线性增长，与超弹性材料橡胶在小变形情况下的曲线变化规律相似；同时从气囊的构成看，它是由内外橡胶层、帘布层复合而成。故而可以将其简化为实心橡胶隔振器，利用ABAQUS求解非线性问题的Newton-Raphson法对气囊力—位移关系曲线进行材料试验数据评估[5]，根据使用情况及精度要求选择不同的本构关系（Mooey-Rivlin、Ogden等方程）进行拟合，得出简化而成的实心橡胶隔振器的模型参数。

根据图8载荷与位移曲线，由静刚度Ks计算公式：

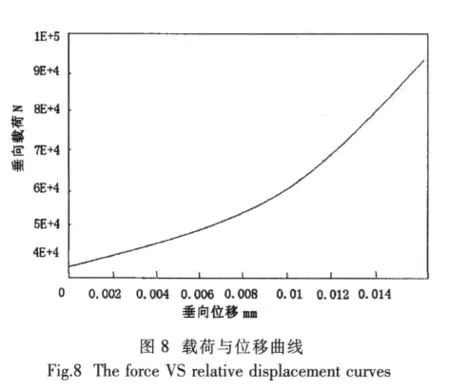
式中：P0为额定静载荷N，ΔP为静载荷增量N，ΔX为静变形增量mm，X1.1为在1.1倍额定载荷隔离器静变形值mm，X0.9为在0.9倍额定载荷隔离器静变形值mm。得出气囊在小变形下的静刚度值为5.33e6 N/m，由（6）式计算出C10为0.711 1，C01为0.177 8。对图2所示的气囊单元重划分，得六面体单元13 200个。这些单元便是简化了的气囊有限元模型，对其附上C10为0.711 1，C01为0.177 8的橡胶参数，按第3节所述方法即可计算出气囊被简化模型代替后的结果，由于篇幅所限在此不再赘述。

此简化方法的使用也有其局限性：简化模型不能模拟出精确模型中气囊疲劳破坏的临界状态；环境温度对气囊内部密闭空气的影响也不能通过简化模型模拟。

6 结 论

通过对两种不同安装方式的囊式空气弹簧隔振器的上述分析，可以得出以下结论：

（1）本文通过数值仿真计算了两种隔振器的模态响应，全面分析了隔振器在随频率变化的动态载荷作用下的薄弱环节和不足之处，对于提高隔振器隔振性能能力有一定的参考价值。

（2）由于降低了隔振器的整体模态频率，安装方式上装配比硫化隔振效果要好。

（3）隔振器的载荷位移变形符合超弹性材料的变化规律，因此在振动特性计算中可以使用实心橡胶模型建立其简化模型。

（4）隔振器简化模型应用有其局限性，适合在小变形的振动计算模型中使用。

[1]师汉民,谌 刚,吴 雅.机械振动系统—分析·测试·建模·对策[M].武汉:华中理工大学出版社,1992.

[2]周相荣,王 强,涂耿伟.弯曲型橡胶缓冲器冲击试验与数值仿真[J].振动与冲击,2007,26(4):97-100.

[3]石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.

[4]吴善跃,黄映云.有限元法计算长方型橡胶空气弹簧隔振器的垂向刚度[J].噪声与振动控制,2002(5):24-28.

[5]刘 展.ABAQUS6.6基础教程与实例详解[M].北京:中国水利水电出版社,2008.