福州市道路交通事故灰色预测模型的构建与实现＊

郑建湖 黄明芳 陈 慧

（闽江学院交通学院 福州 350108）

交通事故的频繁发生不仅造成人员伤亡或物质的损失，也给社会带来巨大的危害性.虽然交通事故的发生有一定的偶然性，但是对于一个地区在较长时域内发生的大量交通事故而言，则有一定的规律性和相对的稳定性，可以根据过去已发生的道路交通事故指标的基础上，对今后几年内交通事故可能发生次数、死伤人数及造成的经济损失作出科学的预测［1－3］，从而为制定交通安全对策提供理论依据.

1 交通事故灰色预测

1.1 交通事故灰色性

交通事故是一个随机事件，其本身具有偶然性和模糊性，交通事故具体的发生时间、发生地点、造成伤害等是无法事先预计的.对于随机过程，人们往往用概率统计的方法进行研究，而概率统计法要求数据量大，因此用于交通事故预测有一定的困难.而灰色系统理论，将随机变量看作是在一定范围内变化的灰色量，将随机过程看作是在一定范围内变化的、与时间有关的灰色过程.在整个道路交通系统中既存在一些确定因素，如道路状况、照明条件等，也存在一些不确定因素，如交通流量、驾驶员心理状态、气候情况等.因此，可以认为整个道路交通系统是一个灰色系统，并可应用灰色系统的理论进行研究和预测.

1.2 常用的灰色预测模型

交通事故灰色预测方法认为，某地区在某时间内的交通事故指标值是在一定范围内变化的与时间坐标有关的灰色量，灰色预测是通过原始数据的处理，发现和掌握系统的发展规律，对系统的未来状态作出科学的预测.目前常用的灰色预测模型有GM（1，1）模型、灰色马尔可夫预测模型等.

GM（1，1）模型适用于具有较强指数规律的序列，只能描述单调的变化过程.灰色马尔可夫预测模型可用于具有一定随机波动过程的预测，但模型应用的难点在于如何对系统状态进行划分，因此对于具有饱和状态的S形序列也难以凑效.Verhulst模型主要用来描述具有饱和状态的S形过程，常用于产品经济寿命、生物生长、繁殖预测等［4］.

近年来，福州市机动车拥有量快速增长，同时交通管理水平也不断提高，导致交通事故4项指标呈现出具有饱和状态的S形过程，故可采用Verhulst模型对其进行预测.

2 交通事故Verhulst预测模型的建立［5］

2.1 数据处理

对X（0）作紧邻均值生成序列

2.2 模型建立

依据上述数据序列，称 X（0）＋aZ（1）＝b（Z（1））2为灰色Verhulst模型，其中a，b为参数.称为灰色Verhulst模型的白化方程，t为时间.

设参数向量

则灰色Verhulst模型白化方程的解为

灰色Verhulst模型的时间响应序列为

2.3 模型精度检验

灰色预测模型要经过检验才能判断其是否合理，模型精度检验方法一般有残差合格模型、关联度合格模型、小误差概率合格模型、均方差比合格模型等.本文采用残差合格模型进行检验.

记交通事故原始数据序列为

灰色模型的预测序列为

残差序列为 ε（0）＝（ε1，ε2，…，εn）.其中

3 实 例

以1995～2004年福州市道路交通事故受伤人数为例，建立灰色Verhulst预测模型.

记交通事故受伤人数原始序列

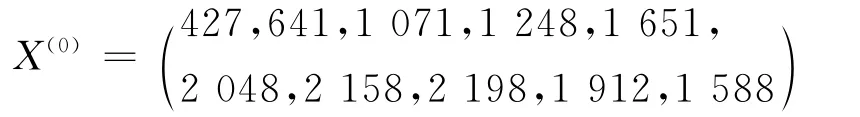
对其进行一次累减生成（1－AGO）序列为

对X（0）作紧邻均值生成序列

因此得Verhulst模型为

其时间响应序列为

Verhulst模型的预测结果如表1所列，其平均相对误差为0.119.

表1 Verhulst模型预测结果

为便于比较，参照GM（1，1）模型建立步骤［6－7］，由1995～2004年福州市道路交通事故受伤人数资料，得到相应的GM（1，1）模型为

表2 GM（1，1）模型预测结果

由于近年来福州市道路交通事故受伤人数波动较大，原始数据最大值是最小值的5倍多，导致灰色预测精度不是太高.比较表3和表4的预测结果可知，Verhulst模型预测结果的平均相对误差为0.119，而GM（1，1）模型预测结果的平均相对误差为0.33，可见Verhulst模型的预测精度明显大于GM（1，1）模型的预测精度.

4 结束语

事故预测的结果有赖于原始数据的精确程度，这是任何一种预测方法都不可回避的一点，在作事故预测时，不得不给予足够的重视.交通安全系统是一个灰色系统，可应用灰色理论进行研究.由于灰色预测模型简单易用，在交通事故预测中得到广泛地应用.GM（1，1）模型适用于具有较强指数规律的单调变化过程，而Verhulst模型适用于非单调的摆动或具有饱和状态的S形过程.值得注意的是，交通事故的影响因素是多方面的，涉及到人、车、道路及道路环境等因素.因此，在进行交通事故预测时，尽可能综合使用多种预测方法，这样预测分析结果才能更加可靠，合乎精度要求.

［1］福州市统计局.福州统计年鉴［M］.北京：中国统计出版社，2006.

［2］岳小泉，丁 艺，黄晓婷.福州市道路交通安全分析及评价［J］.福建农林大学学报，2006，35（4）：435－439.

［3］郑建湖，沈斐敏，陈 袆.福州市道路交通安全现状分析［J］.安全与环境学报，2003，6（3）：65－67.

［4］王福建，李铁强，俞传正.道路交通事故灰色Verhulst预测模型［J］.交通运输工程学报，2006，6（1）：122－126.

［5］刘思峰，郭天榜，党耀国.灰色系统理论及应用［M］.北京：科学出版社，1999.

［6］邓聚龙.灰预测与灰决策［M］.武汉：华中科技大学出版社，2002.

［7］周维新.交通事故灰色预测模型的研究［J］.西安公路交通大学学报，2000，20（2）：73－75.