基于核函数变换的NLPCC分析在洪水分类中的应用＊

刘玉邦 梁 川

(四川大学水电学院1) 成都 610041) (成都理工大学学术期刊编辑中心2) 成都 610059)

洪水的发生和发展具有很强的随机性和不确定性,洪水过程受流域区的天气变化情况、下垫面情况、人类活动等多要素的综合影响.因此,多指标的综合分类方法则成为目前进行洪水分类研究的主要趋势[1-5].目前用于洪水分类的方法很多,如马寅午[6]等、卢正波[7]等的概率方法、模糊聚类方法[8],灰色聚类法[9],王顺久[10]等、董前进[11]等的投影寻踪方法,等等.这些分类方法都在洪水分类中得到了较好的应用,但各有其缺陷和不足.

本文对传统的主成分分析方法进行改进,即将非线性变换和主成分分析法相结合,通过拟线性化变换和降维去噪,得出多维分类指标的一维主成分值,然后通过对每一待分类样本的一维主成分值进行聚类分析,最终得出洪水的自然分类结果.

1 非线性主成分-聚类分析的数学模型及实现步骤

1.1 主成分(PC)分析的数学模型

设有n个样品,每个样品观测p个指标(变量)x1,x2,…,xp,令 xij(i=1,…,n;j=1,…,p)为第i个样本的第j个指标的值,这样得到原始数据矩阵

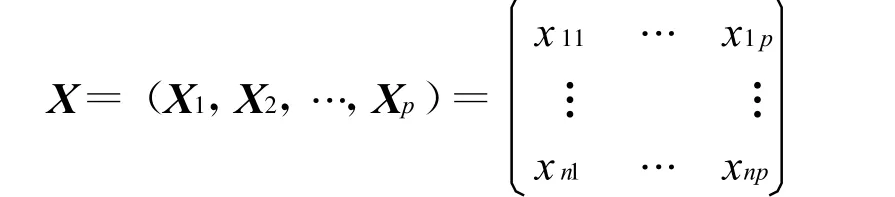
用数据矩阵X的p个指标向量X1,X2,…, XP作线性组合为

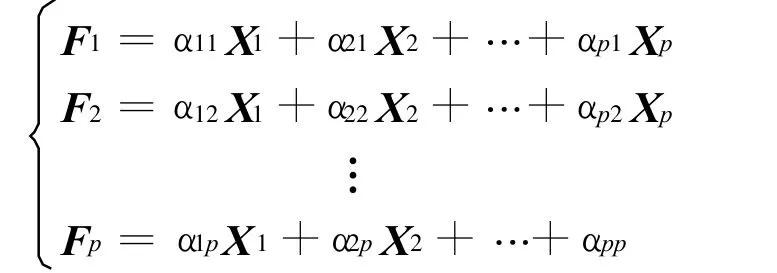
满足上述要求的综合指标向量F1,F2,…,Fp就是主成分.对于原始指标所提供的信息总量,这p个主成分从提取出的信息量用方差来度量,主成分方差的贡献对应原始指标相关矩阵相应的特征值λi而每个主成分的组合系数就是特征值对应的特征向量,方差贡献率为越大,说明相应的主成分反映综合信息的能力越强.

1.2 非线性主成分-聚类(NLPCC)分析的实现

1)原始数据中心化 为了消除原始数据不同量纲、不同数量级差异对评价结果的影响,应首先将原始数据进行量纲一的量化处理.协方差矩阵能较好地刻画原始数据的全部信息,即协方差矩阵的主对角元恰好为各指标的方差,而非主对角元则包含了各指标间相关系数的信息.因此,可将“均值化”方法作为量纲一的量化新方法,即用各项指标的均值去除相应的原始数据,这样得到的新数据的协方差矩阵不仅消除了量纲和数量级的影响,还包含原始数据的全部信息.记经过量纲一的量化处理的数据矩阵为A[12].

2)核函数变换 将上述数据矩阵A中的每一数据元素进行核函数变换,变换函数为高斯核函数记经过核函数的数据矩阵为U.

3)均值化 为进一步消除数量级差异对分类评价结果的影响,可进一步对经过核函数变换后得到的矩阵U中的数据元素进行“均值化”变换.记经过均值化后的数据矩阵为B.

4)对矩阵B进行主成分分析 依据主成分分析数学模型,先求出 B′B的特征值和特征向量,依据公式计算方差贡献率,取 lr＞85%的前几个主成分的和作为原始数据矩阵的主成分,即最后代入相应的分类样本数据,求出各分类样本的主成分值ti.

5)对各分类样本的主成分值进行聚类分析

聚类方法是：(1)将每个样本的主成分值按升序进行重新排列,t1最小,tn最大(n为样本个数);(2)计算相邻主成分值间的差值(i=1,2,…,n),t0=t1;(3)计算δi的累加值其中,i=1,2,…,n;(4)以累加值Y为纵坐标,样本序号N为横坐标绘制散点图.最后根据散点图分布趋势可对样本进行直观分类.

若根据经验或相关专业知识,可以预先确定分类指标标准值,可将分类指标标准的门限值作为一组样本值代入相应的主成分分析模型,求解相应的主成分值,最后将各样本的主成分值直接与分类标准的主成分值进行比较分类.

2 数据选择及模型计算

为便于评价结果的比较,本文选择文献[2]中的数据作为评价数据,其原始数据、分类标准值见表1、表2.

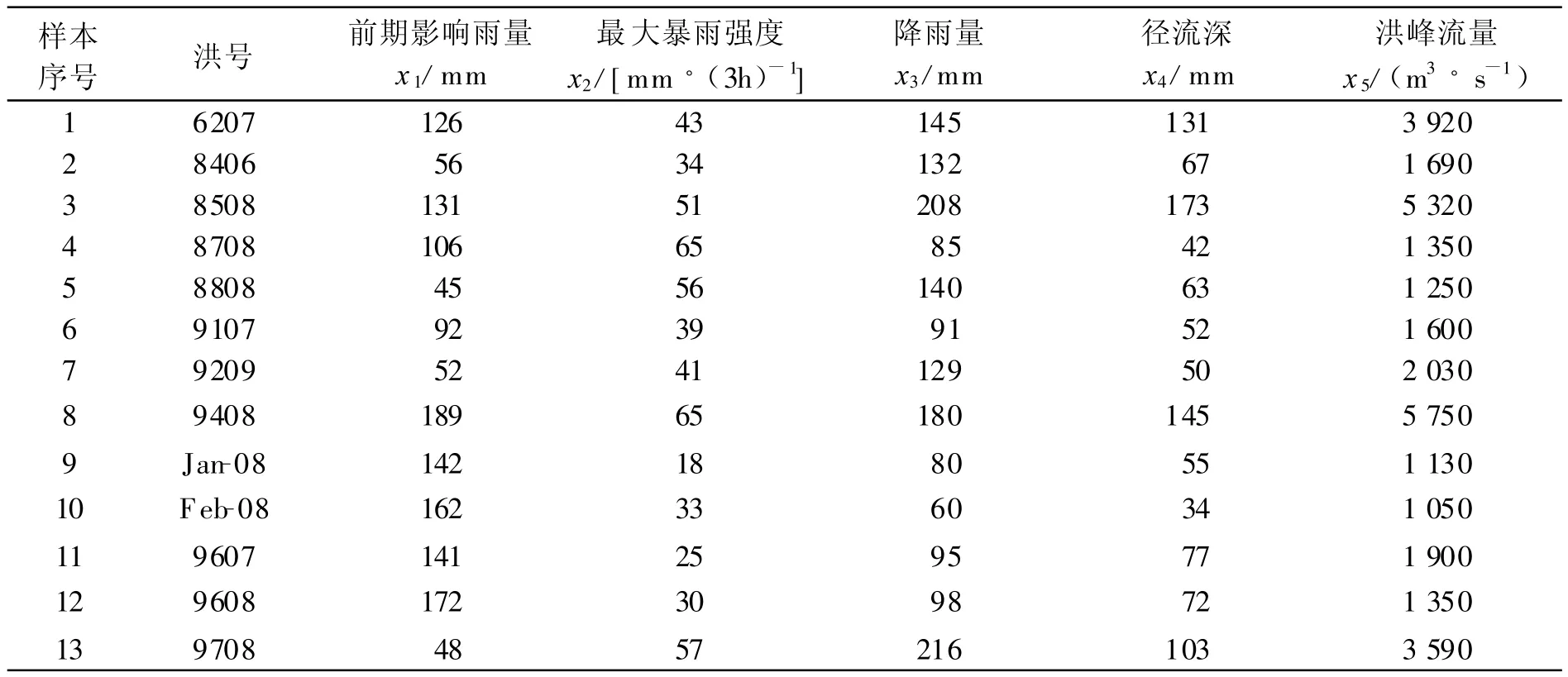
表1 碧流河水库的历史洪水样本

表2 洪水分类指标标准值

按照相应的计算步骤,得到经过均值化、核函数变换和进一步均值化后的数据矩阵

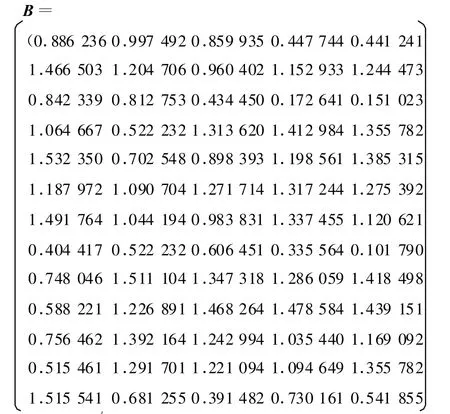
则B′B矩阵的特征值为0.033 428.其中(大于85%),所以选择F1第一主成分为原始数据矩阵的主成分,λ1所对应的特征向量为F1中各变量指标的系数.各样本的第一主成分值为1.937 012,2.288 422,1.449 608,2.327 398,2. 393 906,2.582 52,2.541 853,1.254 806,2.654 418,2.537 727,2.489 044,2.383 785,1.727 012.

相应的,分类指标标准的第一主成分值为1.739 894,2.027 368,2.308 012,2.868 6.将各样本的第一主成分值与分类标准第一主成分值进行比较,可得洪水样本的自然分类结果(见表3),聚类效果图见图1.

表3 洪水过程指标符号量化及分类结果

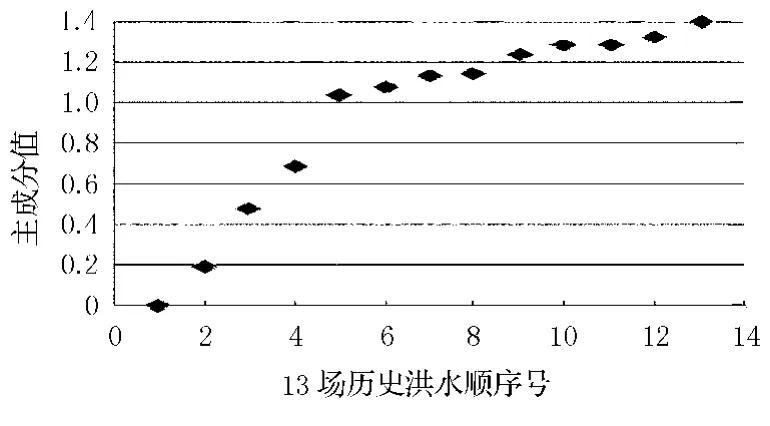
图1 碧流河水库历史洪水非线性主成分-聚类分析效果图

3 结束语

依据聚类效果图并结合主成分值的大小,碧流河13个历史洪水样本可分为四类,即样本号3,8,13为特大洪水,样本号1为大洪水,样本号2为中洪水,样本号4,5,6,7,9,10,11,12为小洪水.这一分类结果和应用集对分析方法所得结果基本是一致的,满足实际应用需要.

从本文所用方法对历史洪水样本进行自然分类的实际来看,可以得出以下几点结论：(1)非线性主成分-聚类分析是一种新颖的分类评价方法,同其他分类评价方法相比,该计算方法既能揭示分类指标空间到类型空间的非线性特征,又不需要复杂的计算机专业知识、优化算法知识和复杂的数学知识,原理清楚,计算简单可行,结果客观有效;(2)从计算过程和计算结果来看,该方法由于采用了两次均值化计算,所以对于所给分类指标门限值变化范围较小时,其分类效果较弱;(3)从实例分析来看,由于分类指标空间到类型空间的非线性特征的差异,不同的非线性变换形式对分类评价结果稍有影响,因而选择适宜的非线性变换函数就较为关键.对于可以预先确定分类指标标准值的,可将指标标准数值判定结果和依据聚类效果图判定的分类结果相互结合,最终得出比较符合实际的分类结果.

[1]张 灵,陈晓宏,翁 毅.人工免疫算法在洪水分类中的应用[J].中山大学学报：自然科学版,2008, 47(5)：110-113.

[2]王文圣.基于集对分析的洪水分类研究[J].高原山地气象研究,2009,29(1)：51-54.

[3]康爱卿,邱 林,张 亭.基于投影寻踪的洪水分类和识别方法研究[J].华北水利水电学报,2009, 30(2)：6-8.

[4]汪丽娜,陈晓宏,李粤安.基于人工鱼群算法和模糊C2均值聚类的洪水分类方法[J].水利学报,2009, 40(6)：743-747.

[5]Ramze M,Lelieveldt B P F,Reiber H C.A new cluster validity index for the fuzzy c2mean[J].Pattern Recognition Letters,1998,19(3-4)：237-246.

[6]马寅午,周晓阳,尚金成.防洪系统洪水分类预测优化调度方法[J].水利学报,1997(4)：1-8.

[7]卢正波,侯召成.洪水聚类有效性分析[J].南水北调与水利科技,2007,5(2)：87-90.

[8]孙 倩,段春青,邱 林.基于熵权的模糊聚类模型在洪水分类中的应用[J].华北水利水电学院学报, 2007,28(5)：4-6.

[9] Lu Hongjun,Chen Yinchuan.The grey clustering method of the evaluati on of flood severity[C]∥Proceedings of Internati onal Symposium on Floods and Droughts.Nanjing：HohaiUniversityPress, 1999.

[10]王顺久,张欣莉,侯 玉.洪水灾情投影寻踪评估模型[J].水文,2002,22(4)：1-4.

[11]董前进,王先甲,艾学山.基于投影寻踪和粒子群优化算法的洪水分类研究[J].水文,2007,27(4)：10-14.

[12]童心安,许 超.基于非线性主成分和聚类分析的综合评价方法[J].统计与信息论坛,2008,23,(2)：37-41.