基于波数积分的点声源海底地震波计算方法研究*
卢再华 张志宏 顾建农
(海军工程大学理学院 武汉 430033)
航行舰船在海底引起的弹性波称为舰船海底地震波,可用于识别舰船目标.目前,舰船海底地震波已经在美、俄水雷的引信中得到应用,并开发出了地震波引信水雷的系列产品[1-2].卢再华等对浅海低频点声源引起的海底地震波进行了时域内的数值模拟,初步确定舰船地震波主要由舰船低频辐射噪声引起,但该数值模拟方法在确定人工边界条件等方面显得较为复杂[3-4].颜冰等采用简正波理论分析了浅海地震波的传播特性,主要研究了海水层中声压的传播损失和频率特性,对海底表面的位移、加速度等地震波动信号尚未做出分析[5-6].本文将舰船地震波简化为液固多层半无限空间低频点声源引起的地震波动问题,采用波数积分方法,通过FFP数值积分求解海底表面声压、位移和加速度幅值,并对海底表面的声传播损失和位移、加速度的频率特性进行分析.
1 低频简谐点声源波动模型
舰船低频辐射噪声包含多个频率成分,简化起见,本文波动模型仅考虑单频简谐点声源.舰船低频辐射噪声引起的波动可由不同频率的简谐点源结果叠加得到.采用由理想流体海水层和均质各向同性海底岩土层组成的液固多层半无限空间简单海洋环境模型,如图1所示.图中:α1,ρ1为海水层的纵波波速和密度;αi,βi,ρi为岩土层的纵波波速、横波波速和密度;d为点源S的深度;为各层深度分别为海水层的势函数以及岩土层的位移势函数,满足亥姆霍兹方程如下
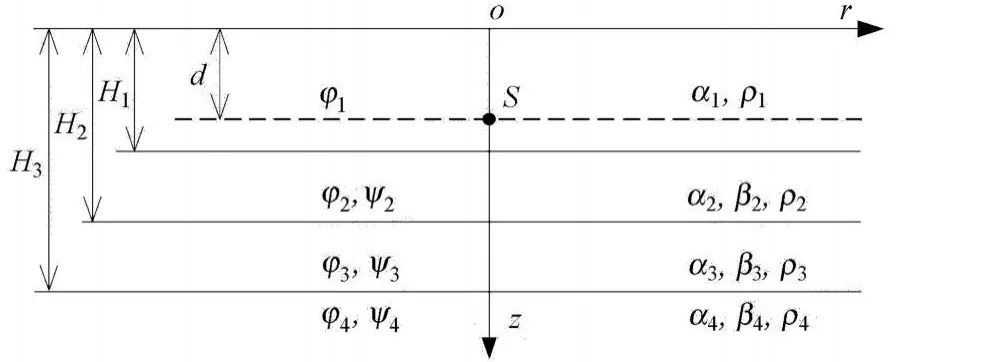
图1 液固多层半无限空间中的简谐点声源
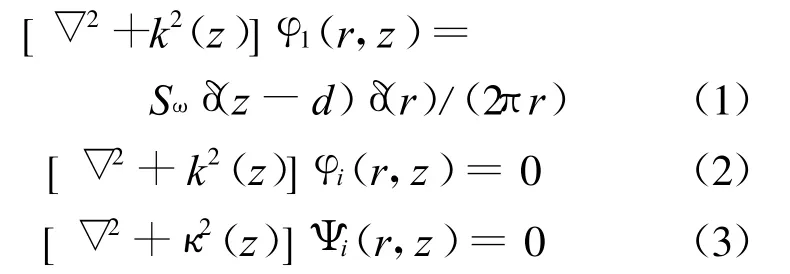
2 简谐点声源波动模型的计算方法
对亥姆霍兹方程式(1)~(3)实施Hankel变换,可得到深度相关的波动方程.以式(1)为例, Hankel变换后的深度相关波动方程为
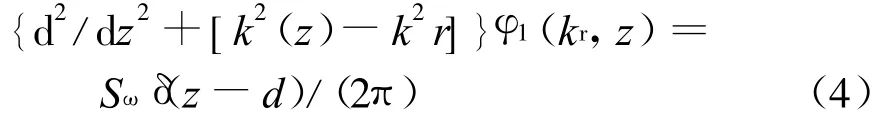
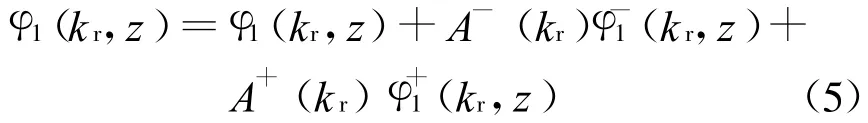
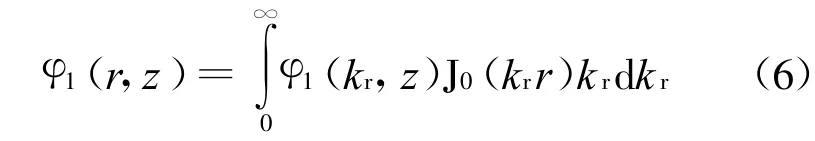
式中:J0(krr)为零阶贝塞尔函数.类似地,可得到各岩土层位移势函数的深度相关格林函数和积分表达式
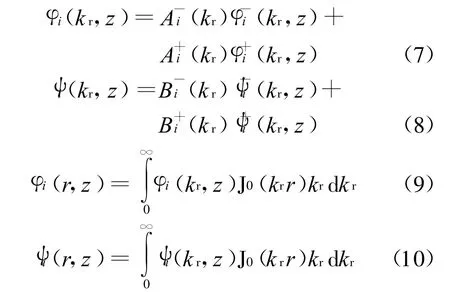
将特解和指数函数形式的通解代入以上各深度相关格林函数,得到
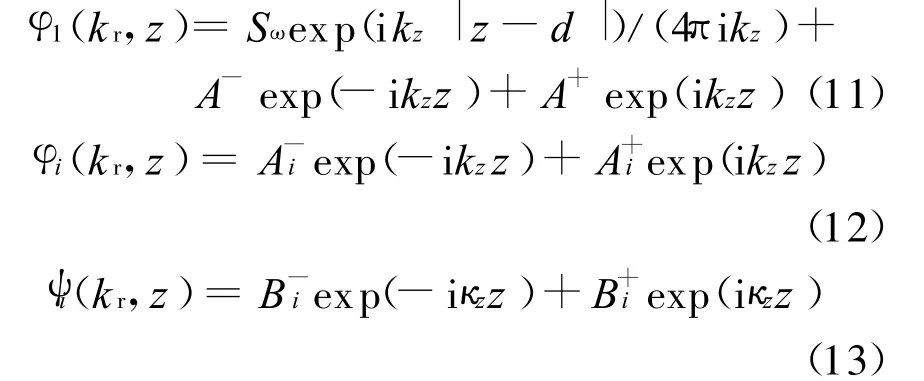
式中:kz,κz分别为各层纵波、横波的垂直波数;分别为纵波和横波的上行波和下行波复幅度.根据位移势函数和位移、声压的关系,可得到海水层竖直位移、声压的深度相关格林函数如下.
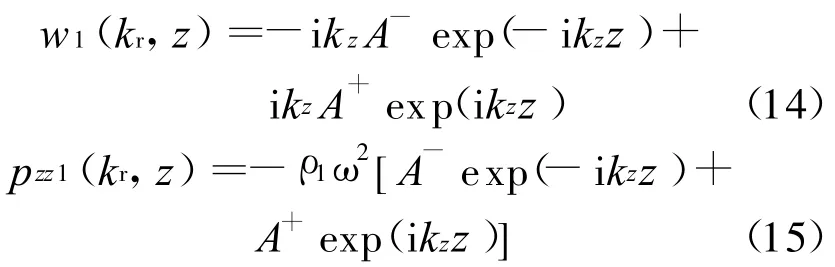
类似地,岩土层竖直位移、水平位移、法向应力和切向应力的深度相关格林函数如下.
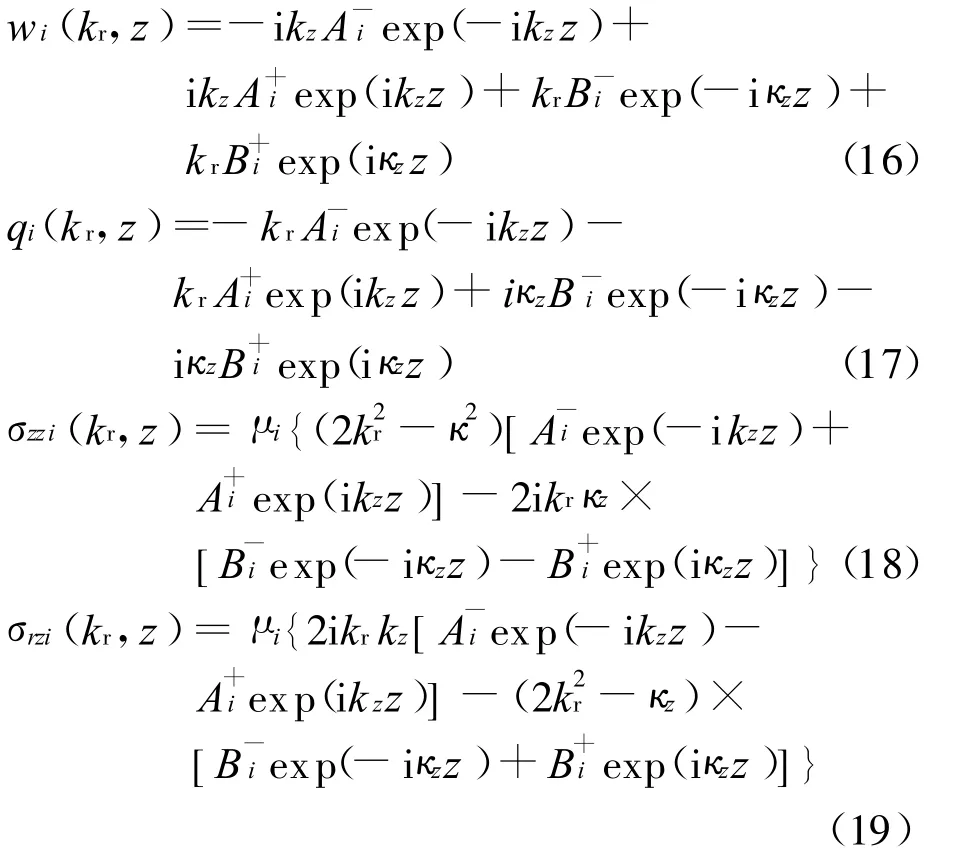
式中:μi为各固体层弹性介质的拉梅常数.最后,将各层位移、声压和应力的表达式代入波动模型的边界条件和层间连续性条件,可得到各层上行波、下行波复幅度未知量,进而求解出各层位移、声压和应力的积分核.对积分核实施反 Hankel变换,即得到类似式(6)的位移、声压和应力的积分表达式.计算此类积分最常用的是FFP算法[7],其基本原理为首先用 Hankel函数展开Bessel函数,然后取代表出射波的第一类Hankel函数并取其近似形式.以式(6)为例,声场势函数的积分表达式可化为
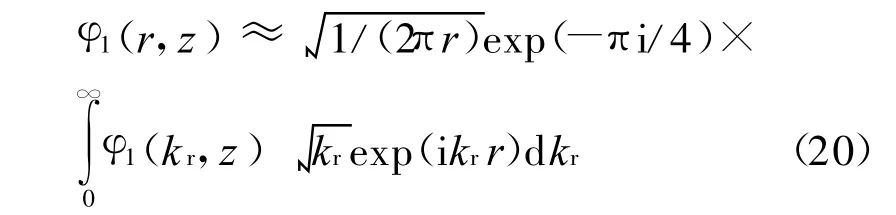
根据DiNapoli和Dravenport的快速声场计算方法,截断积分区域为(krmin,krmax).并离散波数区间和距离如下.
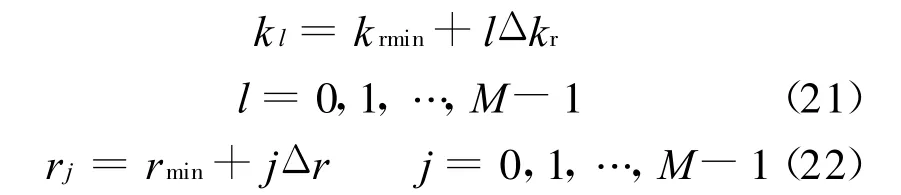
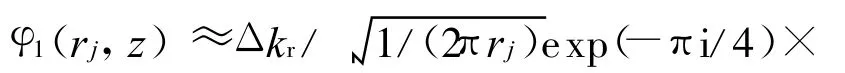
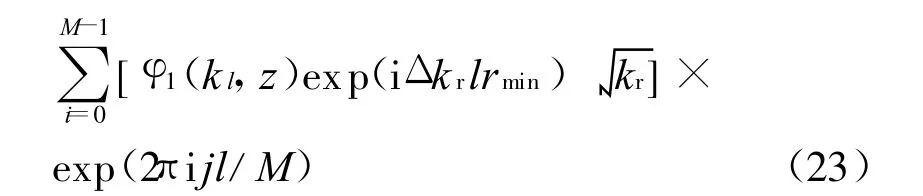
改变积分核函数,可得到位移、声压和应力积分表达式的FFT近似表达式,在此略.
3 计算实例
点源S深度40 m,采用单位压强点源,各频率成分的声压级均为120 dB.算例1分析硬质海底的地质条件,海底岩层仅一层,即表1中的硬质基岩;算例2分析软质海底的地质条件,海底岩层由表1中的砂土层、砂岩和硬质基岩构成.
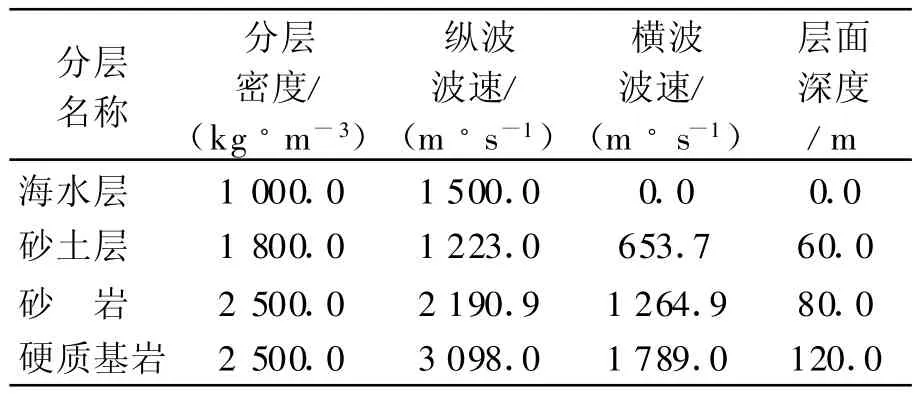
表1 计算参数
图2为20 Hz单频点源硬质海底的声传播损失曲线,可见3个接收深度的声传播损失相差不大,但海底表面声压的各阶简正振型相干性相对其他两个深度较弱.
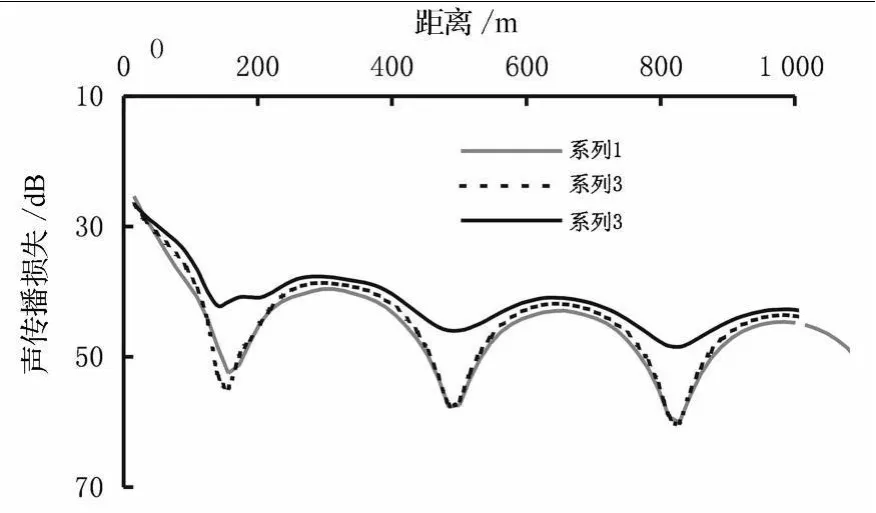
图2 声传播损失曲线
图3~7依次为横距1 000 m处海底表面声压、竖直位移、竖直加速度、水平位移和水平加速度的频率特性曲线.
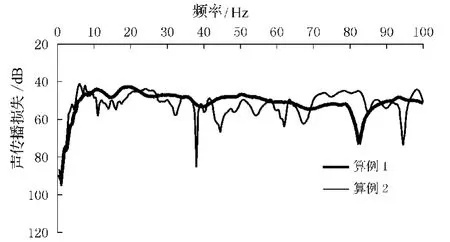
图3 声压频率特性曲线
图3中,2种海底地质条件下的海底表面声压的频率特性曲线差别不大,整体上随频率增大,传播损失逐渐增加.对于位移和加速度而言,由于点源采用的是单位压强,两者物理量不同,故不计算传播损失,改为分析位移、加速度的幅值.考虑到单位压强点源在1 000 m横距处产生的位移、加速度幅值很小,且不同频率存在数量级的差别.为分析方便起见,参照水声学中声压级定义方法[8],定义位移级和加速度级如下.
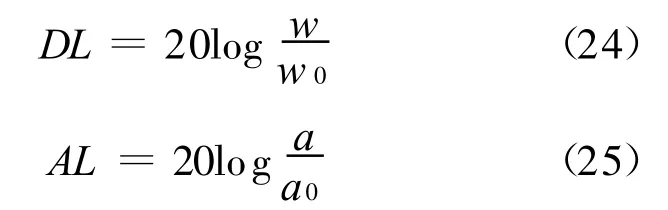
式中:DL,AL分别为位移级、加速度级;w,a分别为接收处的位移、加速度幅值;w0,a0分别为参考位移、参考加速度,本文分别取 10-14m和10-10m/s2.
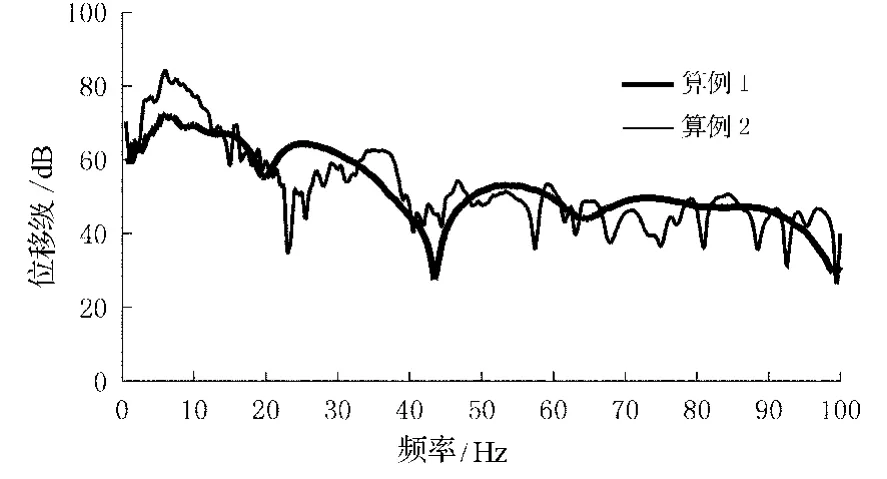
图4 竖直位移频率特性曲线
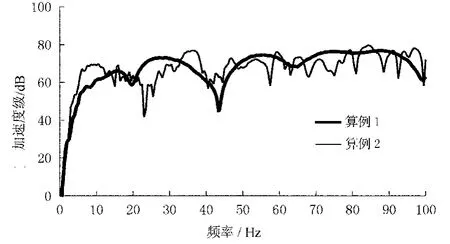
图5 竖直加速度频率特性曲线
由图4可见,随频率增大,两种海底条件的竖直位移均减小,但相比较而言,软质海底更为剧烈.说明远场海底表面竖直位移主要由点声源较低频率成分引起,软质海底尤其明显.另外,软质海底的竖直位移要比硬质海底大得多.
图5中,软质海底竖直加速度的第一个峰值在10 Hz左右,而硬质海底在16 Hz左右,可见,软质海底更有利于声源较低频率成分的传播.
图6~7分别为水平位移、水平加速度的频率特性曲线,其变化规律和竖直方向基本相同.不同之处在于,软质海底的在较高频率处(约40 Hz和60 Hz)存在明显的峰值.
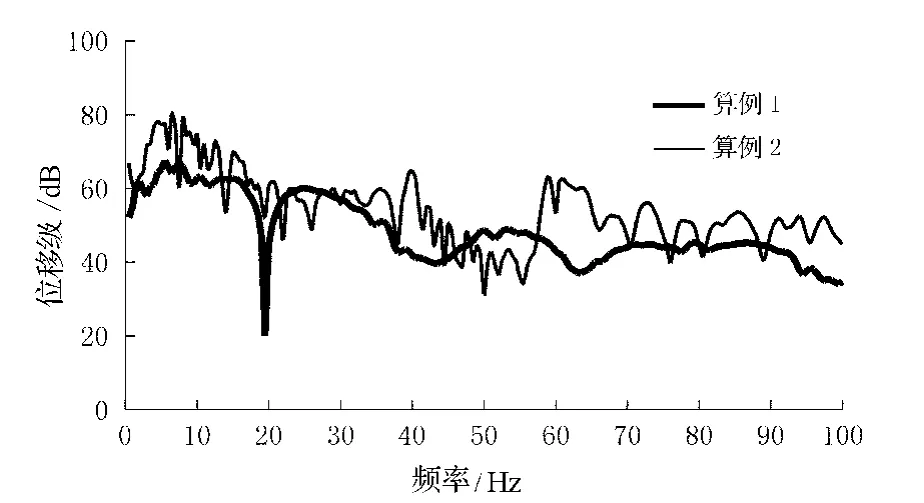
图6 水平位移频率特性曲线
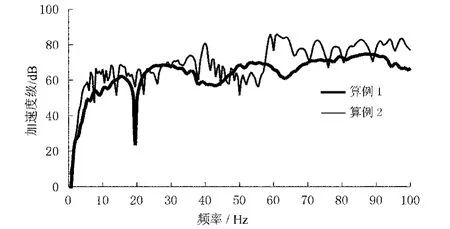
图7 水平加速度频率特性曲线
4 结 论
1)随频率增大,海底表面声压的传播损失逐渐增加.
2)远场海底表面位移主要由点声源较低频率成分引起,软质海底尤其明显.
3)软质海底的位移、加速度总体上比硬质海底大.
4)和硬质海底相比,软质海底更有利于声源较低频率成分的传播.
实际的海洋环境比较复杂,海水层以及海底岩土层对波动传播都存在吸收衰减,海底表面岩层通常为饱水两相介质,本文尚未加以考虑.尤其介质的吸收衰减对点声源较高频率成分的影响较大,因此本文对低频点声源海底地震波的分析还需在考虑介质吸收传播衰减,饱水两相介质等方面做进一步研究.
[1]卢再华,张志宏.舰船海底地震波及其在水雷引信中的应用[J].水雷战与舰船防护,2004(4):25-28.
[2]陈云飞,吕俊军.航行舰船地震波及其在水中目标探测中的应用[J].舰船科学技术,2005,27(3):62-66.
[3]卢再华,张志宏.浅海低频点声源作用下海底地震波的数值模拟[J].武汉理工大学学报:交通科学与工程版,2007,31(4):607-610.
[4]卢再华,张志宏.舰船海底地震波形成机理的理论分析[J].应用力学学报,2007,24(1):54-57.
[5]颜 冰,周 伟.浅海地震波传播的简振波模型[J].武汉理工大学学报:交通科学与工程版,2006,30(5):805-807.
[6]周 伟,颜 冰.舰船低频声传播的海底损失[J].噪声与振动控制,2006(2):62-65.
[7]Dinapoli F R,Deavenport R L.Theoretical and numerical Green's function solution in a plane layered medium[J].J.Acoust.Soc.Am.,1980,67(1):92-105.
[8]刘伯胜,雷家熠.水声学原理[M].哈尔滨:哈尔滨工程大学出版社,1993.

