高温超导电机力矩管漏热分析＊

周 勇 谢 峰 陈 伟 代义军

(武汉船用电力推进装置研究所 武汉 430064)

大容量高温超导电机具有体积小、重量轻、效率高、噪声低、运行稳定等优点,在船舶电力推进、风力发电、机车牵引、冶金矿产等行业具有很好的发展潜力.

国外对高温超导电机的研究十分重视,美、德、日、韩等国[1-4]采取一系列措施,完善体制,增加研究经费,制定研发计划,目前均处于研究开发和试验验证中,并取得了重大的突破.2007年3月美国超导公司完成36.5 MW,120 r/min高温超导电机的出厂试验,该电机的体积和重量分别为常规电机的1/2和1/3.我国于2007年将“兆瓦级高温超导电机的研制”列为“863”计划重点支持项目,目前由我所组织开展研究工作.

高温超导电机与传统同步电机的区别在于转子由高温超导线圈提供直流励磁,磁体工作温度为20～40 K;定子采用气隙电枢;转子内部真空绝热,其典型结构组成如图1所示.其中力矩管位于常温端轴和高温超导磁体之间,起支撑和传递转矩作用.由于力矩管两端存在较大的温差(约270 K),则从常温的端轴必有一定的热量传至低温的超导磁体,并最终由低温冷却系统带走.故在高温超导电机方案设计阶段,为了便于选择制冷机及进行力矩管的结构设计,需要对力矩管漏热进行计算与分析,以供设计者参考.

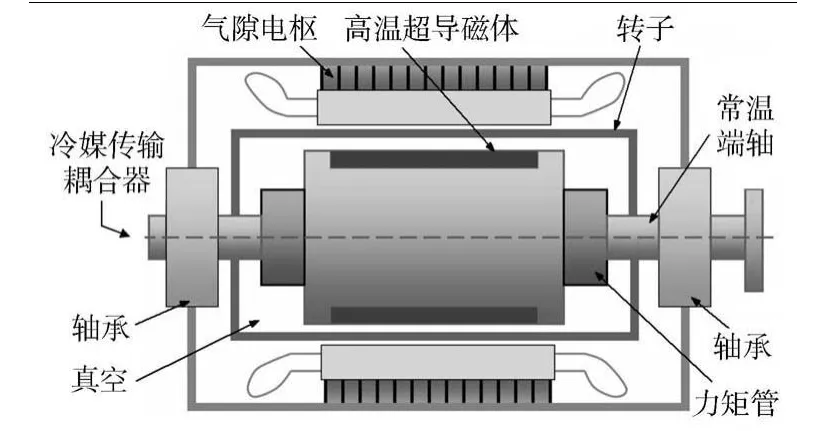
图1 高温超导电机结构组成示意图

1 力矩管结构

在高温超导电机中,力矩管用于连接常温部件与低温部件,是传导漏热的主要部件;同时其又承载磁体重量及传递力矩.综合考虑,力矩管采用高强度低漏热的玻璃钢复合材料,其3D结构示意图如图2所示.

2 力矩管漏热公式

力矩管的使用工况及纤维铺层工艺,可作如下假设：(1)忽略复合材料筒壁的辐射热量损失及热各向异性,仅考虑热量沿力矩管长度方向传递,即温度只沿轴向发生变化;(2)对于复合材料,不同成型工艺的导热系数略有差别,同时,导热系数λ会随温度改变而变化,本次漏热分析时认为导热系数不变;(3)忽略端部厚度,认为是一个长L,截面积为圆环的复合材料筒体(筒体外径D,壁厚为t,截面积S).

力矩管漏热公式推导过程如下[5].

因为温度场是稳定的,则有

对式(1)积分得

对式(2)积分得

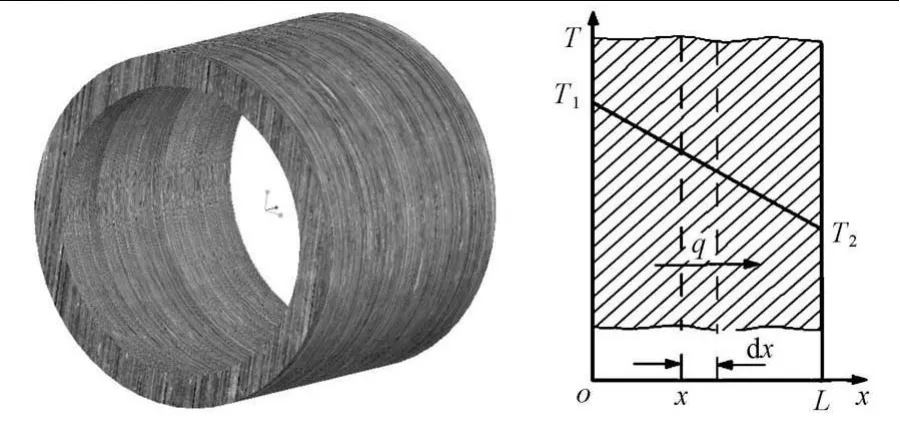
图2 力矩管3D结构示意图 图3 稳定导热图

将积分常数(4)代入式(3),得到温度分布方程为

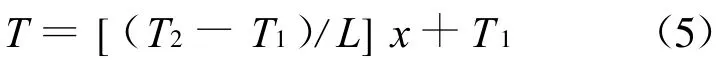
将式(5)代入式(2),可得

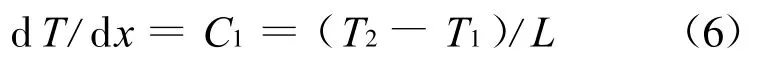
根据傅里叶定律表达

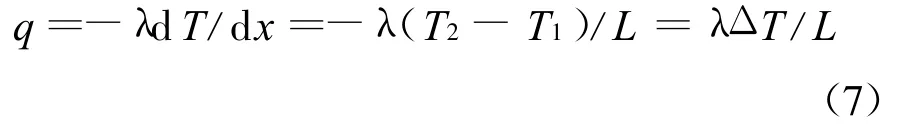
则力矩管漏热计算公式为

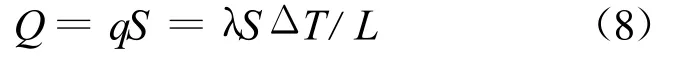
3 复合材料导热系数测试

由式(8)可知,要分析力矩管的漏热,需得知复合材料的导热系数.本研究以力矩管复合材料为测试对象(共3件试样),根据现有条件,应用测试仪对力矩管轴向导热系数进行了测试,测试结果如图4所示.

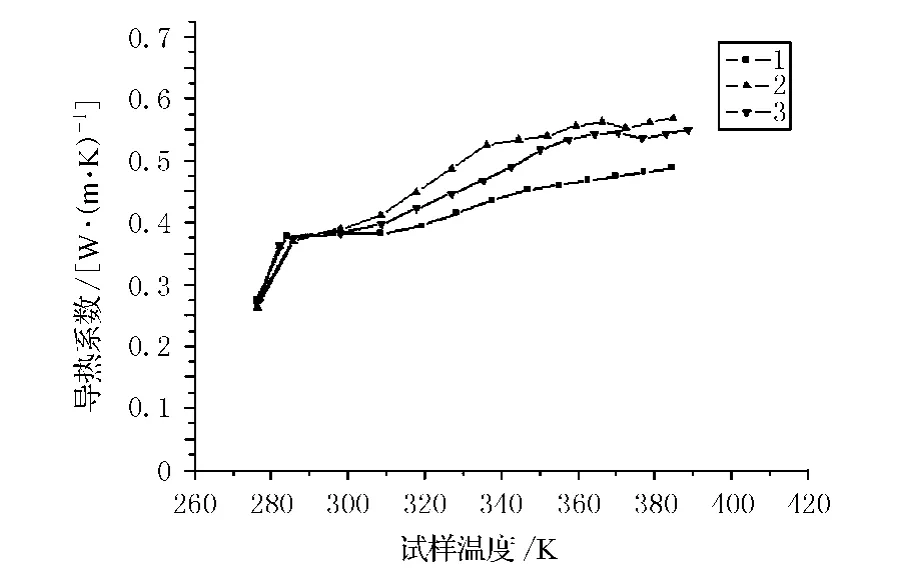
图4 材料导热系数随温度变化关系

由图4可知,各试样的导热系数随温度的升高而增大,其中各试样的导热系数略有不同,这些差异可能与各试样的组成、结构和孔隙度等因素有关.由于复合材料导热系数λ会随温度改变而变化,温度越低,导热系数越小,因此本文漏热计算中复合材料的导热系数采用常温状态(300 K)下3件试样的平均测试值,约为0.37 W/(m◦K),这样力矩管漏热计算值为极大值,可为制冷机选型提供一定的余量.

4 力矩管漏热分析

4.1 理论计算

由式(8)及测试的复合材料导热系数,计算得到力矩管漏热为Q=9.3 W.如果考虑到复合材料导热系数随着温度的降低而下降,热量损失会更小.

4.2 稳态热分析

由上述力矩管工作工况易知：力矩管安装好后,温度缓慢降低至使用温度,其中低温端为40 K,高温端为常温 300 K,此时温度场平衡.于ANSYS中建立力矩管3D几何模型、定义复合材料的热学性能参数、网格剖分及定义温度边界条件后,得到力矩管稳态热分析的有限元分析模型如图5所示.通过稳态热分析,得到力矩管沿轴向的热流密度分布云图,如图6所示.

由于流过力矩管任何一个截面的热量是相等的,故可以取力矩管中心截面来计算力矩管的热量损失.由图6可以看出,流过中心截面的热流密度相等,其大小为

则力矩管漏热仿真计算为

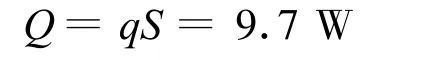
采用有限元计算的热量损失为9.7 W,比理论计算的9.3 W大,这是因为复合材料两端有一个过渡段,其截面积较力矩管中间部分要大,而理论计算时做了简化处理.

图5 力矩管有限元分析模型

图6 力矩管热流密度分布云图

5 力矩管漏热试验验证

5.1 试验装置简介

在力矩管漏热理论计算与稳态热分析的基础上,为了测试力矩管的漏热特性,设计开发了一套力矩管低温测试平台,如图7所示.其中力矩管的低温环境通过制冷机来实现,力矩管两端温度采集通过PT100来实现.

图7 力矩管低温试验平台

5.2 漏热测试结果分析

试验过程中,使力矩管端部温度稳定在40± 2 K,持续时间25 min,试验数据如表1所列.在这段时间内,制冷机的制冷量(100 W)=力矩管传导漏热+试验装置辐射漏热+残余气体漏热+制冷机本身的加热量.

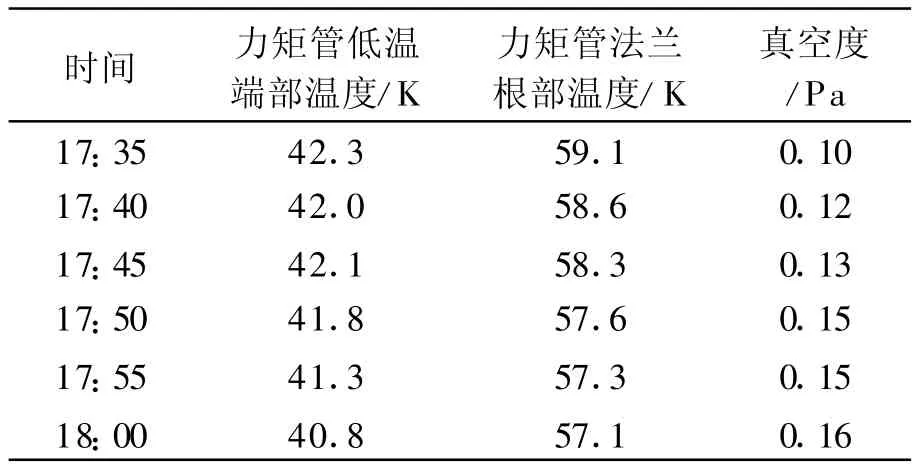
表1 力矩管低温试验测试数据

根据表1所列测试数据计算得知,试验装置辐射漏热为16.8 W,残余气体漏热为14.2 W.在力矩管端部温度稳定的25 min内,制冷机自身的加热时间有 12 min,加热功率为100 W,则25 min内的平均加热功率为48 W.那么,两个力矩管辐射总漏热为21 W,则单根力矩管漏热为10.5 W.相比漏热的理论值与有限元分析值,漏热的实际测量值偏大,这是因为：(1)理论值与有限元分析值只考虑了力矩管的传导漏热,而忽略了辐射漏热;(2)试验测量中,力矩管本身温度有波动,最大波动1.5 K,一部分冷量被力矩管自身释放的热量抵消,而试验数据处理中没有考虑这部分温度波动,造成实测计算值较大.

6 结束语

本文提出了高温超导电机力矩管的结构方案,应用测试仪对复合材料的导热系数进行了测试,并对力矩管的漏热分别进行了理论计算及有限元仿真分析,得出了可供设计参考的力矩管漏热值,具体结论如下.

1)相比力矩管漏热的理论计算,采用有限元方法,由于几何模型建立的更详细,更适用于漏热的精确计算.

2)通过计算与分析,该力矩管结构满足低漏热的要求,达到超导电机力矩管的设计要求.

3)本文所采用的力矩管漏热分析的方法及思路同样适用于其他类似应用场合的力矩管设计.

4)由于力矩管在使用过程中,同时受到弯矩、转矩、冷收缩产生的轴向拉力、高温超导磁体重力及温度载荷,即力矩管的结构设计涉及到多物理场的耦合问题.故要更准确地进行力矩管结构设计及分析,就必须要对力矩管进行热-结构耦合分析.

[1]Snitchler G,Gamble B,Swarn S.The performance of a 5 MW high temperature superconductor ship propulsion motor[J].IEEE Transactions on Applied Superconductivity,2005,15(2)：2 206-2 209.

[2]Frank M,Habelt P,Kummeth P,M assek P,Nick W, Rothfischer H,Schmidt H,Wacker B, Neumǜller H,Nerowski G,Frauenhofer J,Hartig R,Rzadki W.High temperature superconducting rotating machines forship applications[J].IEEE Transactions on Applied Superconductivity,2006, 16(2)：1 465-1 468.

[3]Jo Y S,Ryu K S,Park M.1st phase results and future plan of DAPAS program[J].IEEE T ransactions on Applied Superconductivity,2006,15(2)：678-682.

[4]Maki N,Takao T,Fuchino S.Study of practical applications of HTS synchronous machines[J].IEEE T ransactions on Applied Superconductivity,2005, 15(2)：2 166-2 169.

[5]杨世铭,陶文铨.传热学[M].3版,北京：高等教育出版社,2001.