肋骨分布对肋板声辐射影响及分布优化分析

陈炉云 张裕芳 李英辉

(上海交通大学船舶海洋与建筑工程学院 上海 200030)

加肋板结构广泛应用于船舶和海洋结构.减少结构在中低频率下的声辐射日益受到设计者的关注,改变结构加肋方式是一项减振降噪的重要措施.近年来许多研究成果涉及到肋骨分布对结构的声辐射影响问题.S.Le Moyne等[1]用有限元法和边界元法研究了肋骨对加肋板结构声辐射的3种影响,即振动影响、声源影响和声障影响. R.J.Panuszka[2]用等当量声源理论分析了肋骨对薄板结构的声辐射影响.D.Bojczuk等[3]运用动力响应灵敏度信息进行了肋骨的分布优化研究,并在此基础上对肋骨的外形进行了优化.Luo Jianhui等[4]分析了结构-声耦合系统的内声场优化问题,并用拓扑优化方法将肋骨的分布转化为材料分布问题来处理.

汤渭霖等[5]假设了肋骨对加肋圆柱壳的影响为一个声阻尼,指出肋骨对声辐射功率和结构表面平均声速度的影响.郭新毅等[6]用 Rayleigh＇s积分方程分析了加肋板结构的声辐射功率和声指向性问题,还进行了损伤结构和健康结构的对比.吴文伟等[7]运用Fourier变换分析了等肋距结构的声辐射问题,并指出肋骨对声辐射影响在高频时的远场较明显,改变肋骨惯性矩比改变肋距更明显.黎胜等[8]用FEB/BEM计算了流体加载下的加肋板结构声辐射特性,并分析了板厚、板面积、板长宽比、肋骨惯性矩和间距、边界条件、结构材料和流体材料对声辐射功率的影响.

文章分析了肋骨位置对声辐射的影响并进行肋骨位置和尺寸参数的优化.在优化方程中,声辐射功率被定义为目标函数,并运用遗传算法为搜索策略.在数值计算中,对比分析了肋骨分部优化前后的声辐射功率和场点声压,用以验证优化过程的正确性.

1 加肋板结构的振动分析

采用有限元法来分析动力响应问题时,连续结构受到外力F(x,t)作用,考虑流体对结构的影响可简化为附连水质量形式,在结构域 ΩS内,结构动力响应微分方程可以表达为

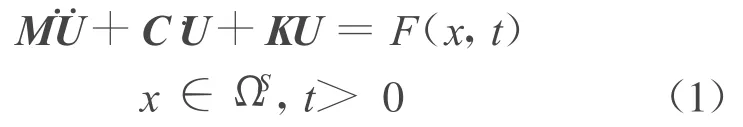
式中：ΩS为结构域;U为节点位移矢量矩阵;M为质量矩阵;K为结构刚度矩阵;C为结构粘性阻尼矩阵.质量矩阵M可写成M=Ms+Mf.其中：Ms为结构质量矩阵;Mf为附连水质量矩阵.

设外力为谐激励力,并可写成如下形式：F(x,t)=f(ω)eiωt,其中f(ω)为谐激励的幅值,ω为圆频率并假设为一常数.节点位移矢量可以写成复变量形式：U(x,t)=u(ω)eiωt,u(ω)为节点位移列向量.

将位移矢量公式和外力公式代入式(1),可消去时间变量并得到如下的算子方程.

式(2)可简化为：A(ω)u(ω)=f(ω).其中：A(ω)= -ω2M+iω C+K,得到节点位移矢量矩阵：u(ω) =[A(ω)]-1f(ω).定义节点的速度矢量为v(ω),并可写成：v(ω)=iω u(ω).在结构与流体的交界面上,节点的法向速度矢量可写成

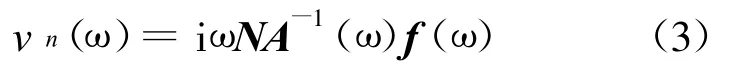
式中：N为法向矢量矩阵,它与结构的表面形状有关,节点的法向速度矢量在声边界元法分析中作为边界条件.

2 声辐射方程

在结构-声辐射计算中,假设只考虑加肋板的上表面与流体接触,此时板结构可认为是镶嵌于无限大的障板上,肋骨只对结构的振动有影响.边界元模型可以用Rayleigh积分方程来求得.采用边界元法分析结构声辐射问题具有许多的优点,不会生成复杂的三维声模型.在中低频下的外场声辐射分析中,半空间内的流场中的声压可写成

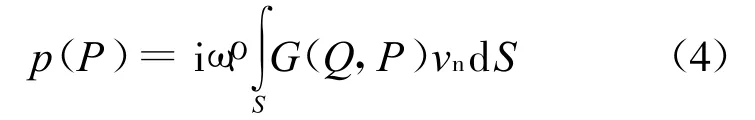
式中：S为流固交界面;ρ为流体的密度;ω为声波圆频率;vn为结构表面节点法向速度;Q为结构表面上的任意点;P为流场或结构表面上的任意点;G(Q,P)是半空间内的格林函数,可写成

式中：r=|Q-P|.

在声场中,描述能量流在假定的积分面上的属性可以用辐射声功率来表示,记声辐射功率为∏,其大小为

式中：E为声场空间上假定的积分面.如不计声能量在流体中传播时的损失,同时忽略结构对声能量的吸收.这样在外声场中的声能量与结构表面的声辐射能量相等.

对于连续振动结构体,其表面的声辐射功率为

式中：S为结构-流体交界表面;pf为结构表面声压;v＊n为结构表面法向共轭速度.在流体阻尼阵与流体附加质量阵比值很小时,式(1)即为声固耦合方程的简化形式,此时结构表面节点声压与节点法向速度满足：pf=ρ cvn,且pf与vn间的相位角为0.将式(3)代入可得到结构表面处的声压方程：pf=iω ρ cNA-1f(ω).

在边界元分析中,将结构的积分表面离散成M个单元和N个节点.此时结构的辐射声功率为M个单元的声辐射之和,表示为：式中：Ωj为第j个单元积分面为第j单元的法向速度,它大小由单元上的节点法向速度决定.此时结构表面处的声辐射功率方程写成离散形式为

3 声辐射功率优化方程

建立了结构的声辐射功率方程以后,将结构-声优化问题转换为在设计空间里搜索一组设计变量使得结构表面的声辐射功率最小的问题.将声辐射功率替代声压作为结构-声优化问题的目标函数有许多优点,如将矢量参数的求解变成标量参数的求解,不需要求指定场点处的声压等等.如果将声辐射功率在一定频率段下的平均值定义为目标函数,则声辐射优化方程可写成为

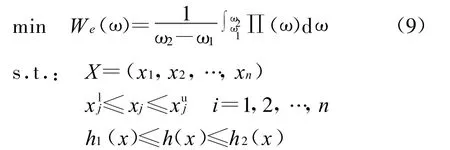
4 数值算例

为了证实肋骨分布对声辐射影响及分布优化过程,在算例中分别运用有限元法和边界元法,最后集成两种方法结合运用遗传算法进行肋骨分布优化.

4.1 模型描述

一个处于水中的加肋板结构受到谐外力的作用,如图1所示,加肋板结构的4个角点为绞支约束支持,结构的上表面与水接触.结构的设计参数为

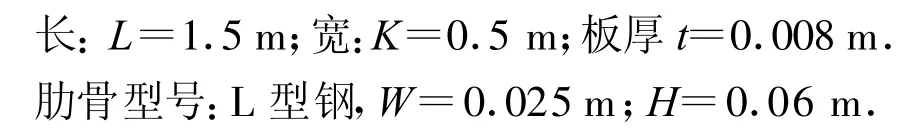
在初始设计中,板上有4根长为0.5 m等距分布的肋骨,肋骨间距为a=b=0.3 m,板架结构对称于YOZ平面.

图1 加肋板结构

在有限元模型中,加肋板结构被离散成1 280个节点和1 280个单元(包括80个梁单元),如图2所示.

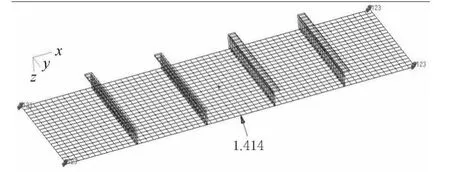
图2 加肋板结构有限元模型

结构的材料为钢,其力学特性为：密度ρ= 7 800 kg/m3;弹性模量E=210 GPa;泊松比μ= 0.3.结构的总重量为54.2 kg.结构的第一阶频率为ω=7.9 Hz.

水的声学属性为：密度ρ=1 025 kg/m3;水中声速为c=1 500 m/s;声功率参考值W0=1× 10-12W;声压参考值p0=1×10-6Pa.

外激励力的中心频率为10 Hz,力的作用点位于长边的中部,如图2所示,大小为＜0,1.0, 1.0＞N.

4.2 肋距对声辐射功率的影响

用有限元软件MSC/Nastran软件来计算结构动力响应,采用边界元计算结构的声辐射.

改变肋距可以计算得到不同的加肋板的声辐射功率,频率响应计算的频率从1～201 Hz,步长为2 Hz.声功率计算的频率从1～200 Hz,步长为2 Hz.图3为肋距改变前后的声辐射功率对比图,新的肋距为a=b=0.25 m.图4为肋距改变前后的声辐射功率对比图,新的肋距为a=b=0.35 m.

图3 声功率对比

图4 声功率对比

4.3 肋骨分布优化

通过调整肋骨的间距可以减少结构的声辐射功率,这是肋骨分布优化的出发点.同样,改变肋骨尺寸也可降低声辐射功率.在声辐射优化分析中,设加肋板结构的总重量保持不变,肋骨的方向也是不变的,同时板的厚度也是不变的.

在优化中将肋骨的位置和尺寸参数定义为设计变量,并设肋骨不会分布在板的边缘上.在优化分析中,通过集成Nastran和Sysnoise,应用遗传算法进行声辐射优化.遗传算法有以下特点：在复杂优化问题中具有较强的全局搜索能力;不需要计算目标函数的导数;适合于优化连续和离散混合参数问题;适用并行计算处理等等.

4.3.1 肋骨分布优化 在这种优化模式中,只改变4根肋骨的位置.优化后,肋骨间距为：a=0.2 m,b=0.45 m.图5所示为结构在优化前后的结构声辐射功率,其最大辐射功率减少了约 8 dB.图6所示为在场点(0,0,20)处优化前后的声压,在数值上有一定的减少.

图5 声功率优化

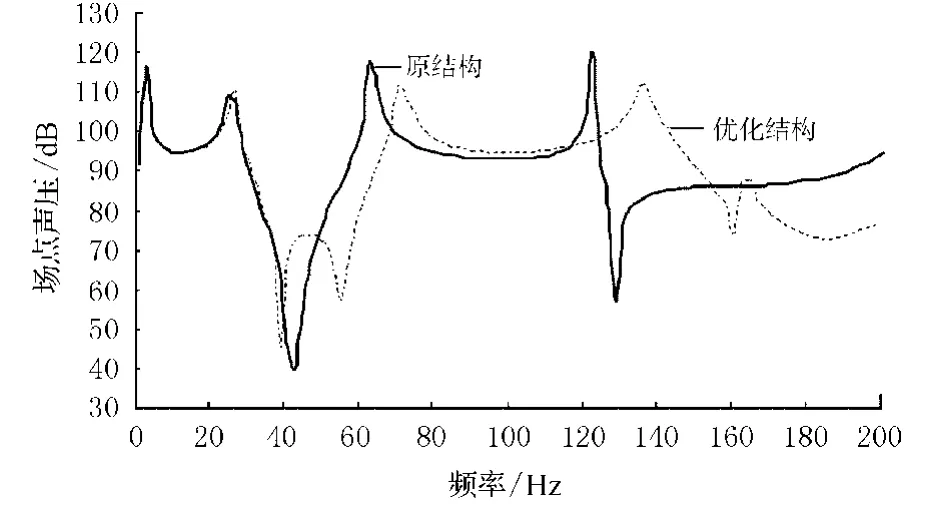
图6 场点声压

4.3.2 肋骨分布与尺寸联合优化 在这种优化模式中,是结合分布优化和尺寸优化的进行的肋骨优化.优化的约束还包括肋骨的尺寸约束,同是确保总质量不超过原结构.定义L型肋骨的宽度W和高度H为设计变量,并满足：0.01 m≤wi≤0.04 m,i=1,2;0.04 m≤hk≤0.1 m,k=1,2.结构的总质量满足：

优化后的肋骨间距为：a=0.25 m,b=0.475 m,肋骨尺寸为：w1=0.032 m,h1=0.044 m;w2 =0.038 m,h2=0.065 m.结构的质量是53.8 kg,优化结果满足约束条件要求.

图7所示为结构在优化前后的结构声辐射功率,其最大辐射功率级减少了约18 dB.图8所示为在场点(0,0,20)处优化前后的声压,在数值上有一定的减少.

对比图5～图8,通过优化以后结构的声学性能有了改善.而结合分布优化和尺寸优化的效果更为显著.这表明将尺寸优化和分布优化相结合起来将能提高优化效果.

在实际工程中,出于对设计、制造等多方面考虑,结构的肋骨的间距不可能随意变化;同理,实际结构的肋骨一般也必须选自标准型材.特别是梁尺寸的选取还有一些限制,其设计变量是不连续的,对于这方面的问题需要进一步研究.因此,在实际工程中不能完全采用优化结果,优化结果对实际工程具有一定的参考意义.

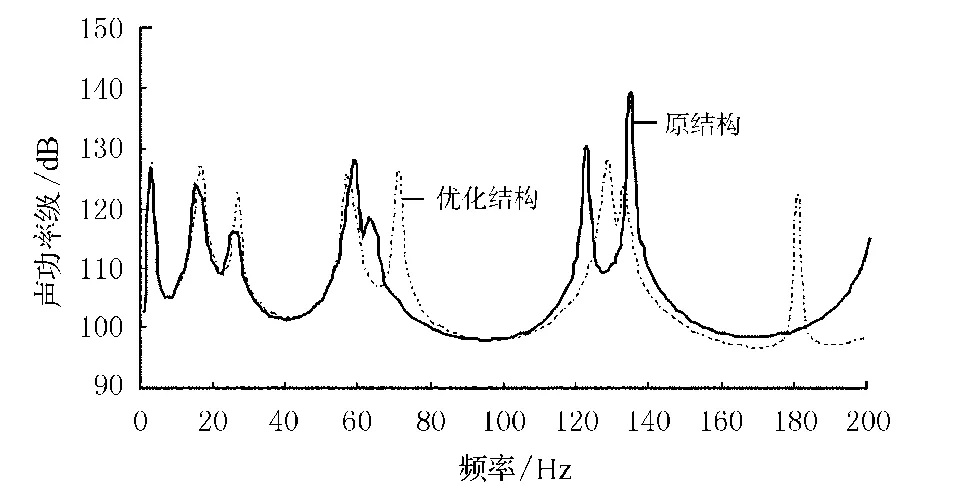
图7 声功率优化

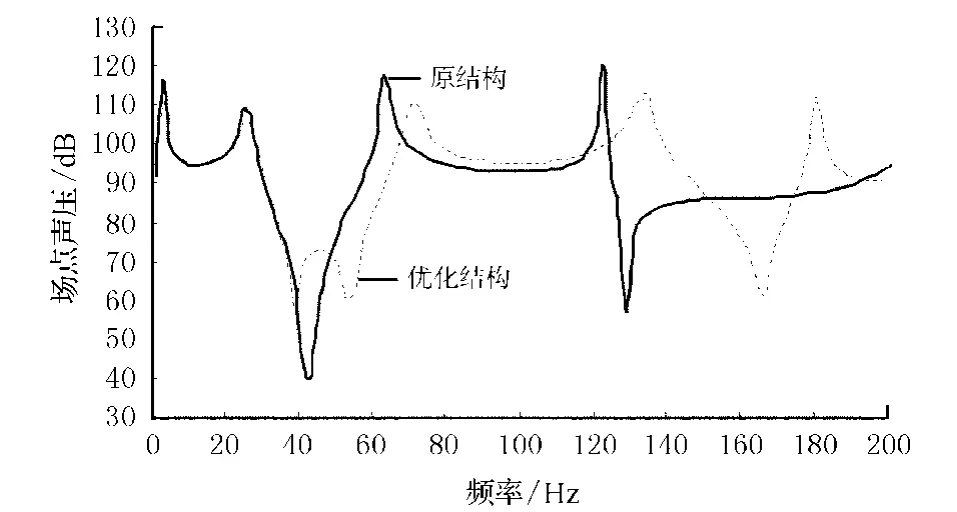
图8 场点声压

5 结束语

文章用有限元法和边界元法分析了加肋板结构在单频率简谐激励作用的声辐射功率问题.应用遗传算法,通过优化肋骨分布位置和尺寸来实现改变结构的声辐射模态并减少声辐射.数值计算表明,通过分布优化后其声辐射功率的最大峰值有了明显减低,同样在声场点的声压有了减少.进一步对比表明,将尺寸优化和分布优化相结合后的优化效果更为显著.

[1] Moyne S L,Tebec J L,Tawfiq I.Acoustical influence of stiffeners on acoustic radiation of plates[J]. Mechanical Systems and Signal Processing, 19, (2005)：195-212.

[2]Panuszka R J.The influence of stiffness and boundary conditions of thin rectangular plates on radiated acoustic power[J].Applied Acoustics,1995(46)：345-362.

[3]Bojczuk D,Szteleblak W.Optimization of layout and shape of stiffeners in 2D structures[J].Comput Struct,2008,86(13-14)：1 436-1446.

[4]Luo Jianhui,Hae Chang Gea.Optimal stiffener design for interior sound reduction using a topology optimization based approach[J].Journal of Vibration and Acoustics,2003,125(3)：267-273.

[5]汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1)：1-5.

[6]郭新毅,洪 明,李艮田.含损伤加筋板结构辐射声功率及指向性变异研究[J].船舶力学,2005,9(4)：119-129.

[7]吴文伟,冷文浩,沈顺根.具有等间距相同加强筋板的声辐射[J].中国造船,1999,146(3)：72-81.

[8]黎 胜,赵德有.流体加载下加肋板结构的声辐射特性研究[J].应用声学,2000,19(6)：28-39.