等离子射流与渐扩边界中液体工质相互作用特性的模拟实验*
张 琦,余永刚,陆 欣,刘东尧
(南京理工大学能源与动力工程学院,江苏 南京210094)
电热化学发射技术中等离子体发生器产生的等离子射流既是完成能量转化的工作介质,也是发射药化学能释放的点火源,因此脉冲等离子射流的特性及其与发射药的相互作用机理是电热化学发射中的关键技术之一[1-4]。以液体工质电热化学发射为工程背景,K.K.Kuo 等[5]利用高速摄影和脉冲X 光照相研究了等离子体射流和液体之间的相互作用过程,给出了等离子体射流在液体中形成的Taylor 空腔扩展过程以及等离子体的强度分布规律。A.Arensburg 等[6]采用阴影成像技术研究了等离子体射流在水中的连续膨胀过程,定量研究了射流的运动速度以及两相作用面上液体卷吸的质量流量和液体卷吸形成液滴的过程。周彦煌等[7]研究了等离子射流与圆柱形观察室内的液体工质的相互作用特性。
在整装式液体工质电热化学炮中,由于Taylor 空腔的发展及Helmholtz 不稳定效应的激励,其扩展过程随机脉动性较大,进而影响到液体工质电热化学发射系统的燃烧稳定性,为此R.L.Talley 等[8]提出利用边界形状来约束Taylor 空腔的发展思路。余永刚等[9]研究了圆柱形和圆柱渐扩形2 种观察室中等离子射流与液体工质的相互作用问题。本文中在此基础上,针对2 种圆柱渐扩型观察室,研究不同放电电压、不同喷口直径、不同渐扩结构下等离子射流与液体工质的相互作用特性。
1 实验装置
实验装置如图1 所示,主要由等离子发生器、脉冲功率源和观察室组成。等离子发生器包括1 个毛细管、1 对电极以及毛细管外的绝缘体、金属壳体。通过对该毛细管大功率放电使毛细管材料烧蚀、电离形成等离子体,将电能转化成热能。实验采用的毛细管是长73 mm、内径6 mm 的聚乙烯管,两端通过电极连接到脉冲功率源,其中阳极端保持密封,阴极端开孔作为等离子体流出通道,并与观察室相连。脉冲功率源由电容储能的脉冲形成网络(PFN)组成,毛细管作为该放电回路的负载,如图2 所示。储能电容器组的容量为46.5 μF,电感器电感为35 μH,可以通过对电容器组的充电电压和放电回路参数来调整等离子体的输出强度。为保证放电回路的可靠放电,在放电开始时用细的金属电爆炸丝将阳极和阴极连接起来,电流首先使金属丝电爆炸形成等离子体,然后再烧蚀毛细管壁面材料。阴极喷嘴预先用金属膜片密封,防止液体倒流,并使毛细管内等离子射流达到一定压力才开始喷射。观察室为圆柱渐扩型,由透明有机玻璃制成,内部充满液体模拟工质,考虑到安全性,选用密度和粘度与液体药相近的水作为模拟工质。为防止等离子射流在液体工质中膨胀、扩展时压力过大而损坏观察室,观察室顶端开口与大气相通。
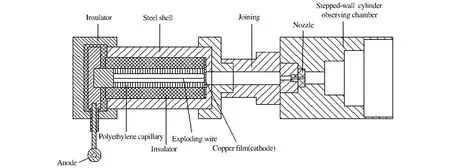
图1 实验装置示意图Fig.1 Experimental apparatus
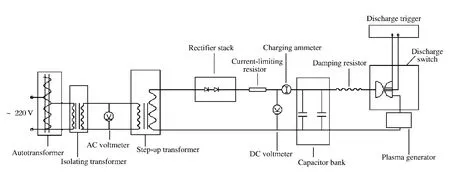
图2 脉冲形成网络电路图Fig.2 Pulse-forming network setup
为消除重力对射流结构的影响,实验装置垂直放置,等离子体竖直向上喷射。实验中采用FASTCAM-ultima APX 数字高速录像系统记录等离子射流与液体相互作用过程,同时毛细管内的压力采用CY-YD-205 型压电式压力传感器测量。
2 实验结果与讨论
实验中使用2 种圆柱渐扩型观察室,总长均为98 mm。第1 种观察室共4 级,第1 级直径D=18 mm,以后每级直径比前1 级增加12 mm,1 ~3 级长L 均为20 mm,第4 级长为38 mm;第2 种观察室共3 级,前3 级直径与第1 种的前3 级直径相同,但前2 级长L 变为30 mm。将等离子发生器固定在工作台上与脉冲形成网络连接,将圆柱渐扩型观察室与等离子发生器相连。准备完毕后对电容器组充电,达到需要的电压值后切断电源,再启动触发间隙放电开关进行放电。
针对4 级圆柱渐扩型观察室,在放电电压Uc=2 500 V,喷嘴直径d0=2.0 mm 工况下,由压电测压系统测出该毛细管内典型p-t 曲线,如图3 所示。由图3 可知,在放电阶段,毛细管内的压力迅速增大,膜片破裂后压力迅速下降。实验表明放电电压越高,毛细管内的最大压力越大,毛细管内的压力增长和衰减也越大。
2.1 等离子体射流在液体中扩展的典型过程
图4 是Uc=2 700 V,d0=2.0 mm 时,等离子体射流在渐扩结构因子ΔD/L=0.4 时的圆柱渐扩型观察室中扩展的序列过程。其中ΔD 为每级圆柱台阶直径增量,L 为对应台阶的长度。
从图4 中可以看出,渐扩边界对等离子体射流在液体工质中扩展时形成的Taylor 空腔有径向诱导作用,Taylor空腔将沿着渐扩边界逐级扩展,在渐扩处会发生回流卷吸现象。实验中观测到Taylor 空腔前端等离子体与液体间的传热效应较强,气液界面处由电爆炸丝及电极形成的金属等离子体以及毛细管等离子体被迅速冷却形成黑色物质,如图4 中t=4.5 ms 时所示。此外,Taylor 空腔扩展过程中,前端面受到液体的压缩作用,轴向位移增量逐渐变小。当喷嘴直径缩小到d0=1.5 mm 时,Taylor 空腔前端面甚至会出现“倒退”,典型过程如图5 所示(Uc=2 700 V,d0=1.5 mm,ΔD/L=0.4),相应的轴向位移x 与时间t 的关系如图6 所示。从波动力学和湍流力学理论来看,Taylor 空腔在渐扩边界的液体工质中扩展时将产生复杂的波系结构,经不同边界面反射形成“稀疏”或“压缩”作用,决定了前端面边界的发展状况及位移特征。此外,Taylor 空腔在扩展过程中,由于Taylor-Helmholtz 不稳定效应,Taylor空腔扩展到某一位置时,前端面及其不稳定。由于湍流耗散效应,此时Taylor 空腔前端的等离子射流动能几乎耗尽,而Taylor 空腔上游液体的压力较大,于是就出现了位移增量减小的现象。当喷嘴直径较小时,等离子射流动能也就较小,在液体静压的作用下某时刻Taylor 空腔前端面就出现了“倒退”。当放电电压较大时,等离子射流动能变大,在观察窗尺度范围内,Taylor 空腔前端面等离子射流动能未耗尽,就不会出现“倒退”现象。
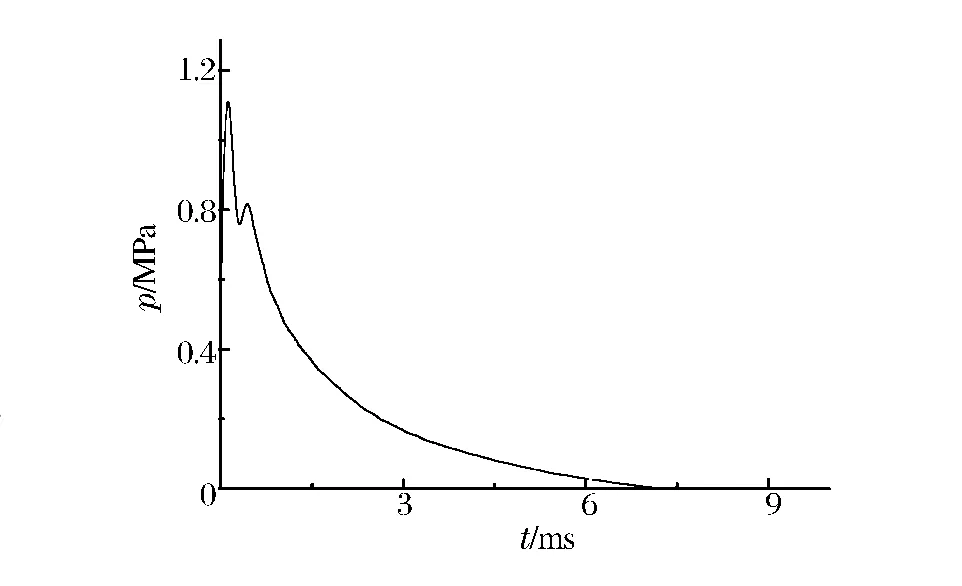
图3 毛细管内的p-t 曲线图Fig.3 p-t curve in capillary

图4 等离子体射流的典型扩展过程(ΔD/L=0.4)Fig.4 Plasma jet propagation in liquid medium(ΔD/L=0.4)

图5 Taylor 空腔扩展过程Fig.5 Propagation of Taylor cavity
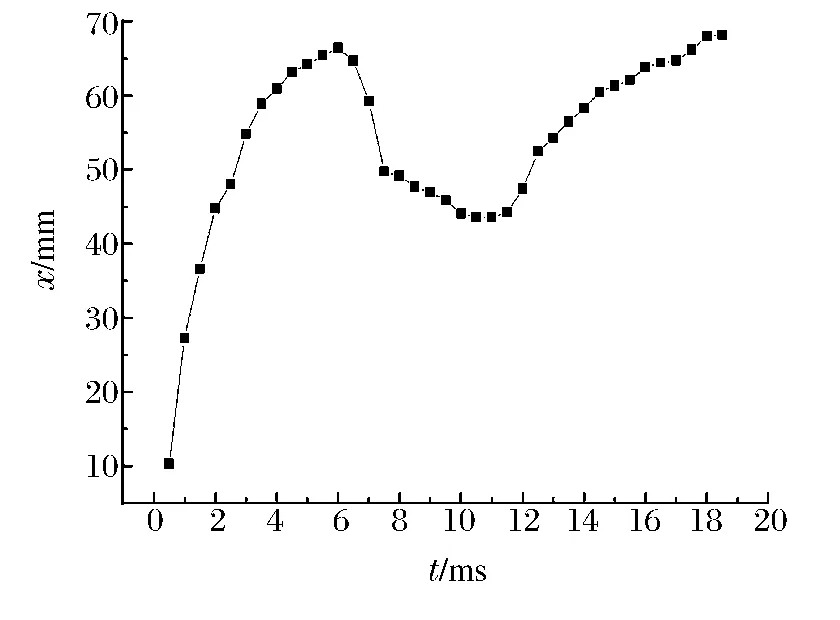
图6 等离子体射流前端面轴向扩展的x-t 曲线Fig.6 Axial x-t curve of plasma jet
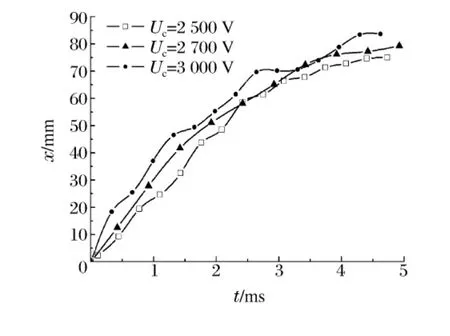
图7 不同放电电压下的x-t 曲线Fig.7 x-t curves at different discharge voltages
2.2 放电电压对等离子射流在液体工质中扩展特性的影响
Uc分别为2 500、2 700 和3 000 V 时,Taylor 空腔在圆柱渐扩型观察室中扩展的轴向位移与时间的关系如图7 所示,其中d0=2 mm,ΔD/L=0.4。
由图7 可知,在相同时刻,放电电压越大,Taylor 空腔的轴向扩展位移越大。Uc分别为2 500、2 700、3 000 V 时,Taylor 空腔扩展到第2 级台阶(x=30 mm)所用时间分别为1.3、0.99、0.76 ms;扩展到第3级台阶(x=60 mm)所用时间分别为2.57、2.50、2.16 ms。说明等离子射流动能越大,其轴向扩展能力越强,但由于Taylor-Helmholtz 不稳定效应,Taylor 空腔轴向扩展位移具有波动性。
2.3 喷嘴直径对等离子体射流在液体工质中扩展特性的影响
当放电电压不变,即Uc=2 700 V 时,仅改变喷嘴直径,分别为2.0 和1.5 mm,观察Taylor 空腔在观察室(ΔD/L=0.4)中扩展的轴向位移和速度变化特性,如图8 ~9 所示。
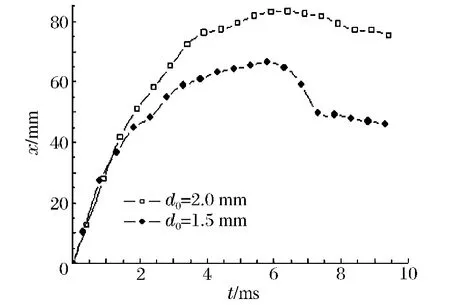
图8 不同喷嘴直径下的x-t 曲线Fig.8 x-t curves at different nozzle diameters
从图8 中可以看出,在Taylor 空腔扩展到34 mm之前,d0=1.5 mm 时的Taylor 空腔轴向扩展位移略大,这是由于喷嘴变小时,毛细管内的最高压力变大,使初始一段时间喷嘴较小的Taylor 空腔轴向扩展速度较大,Taylor 空腔与液体工质的接触面积与其自身的体积比将增大,Taylor 空腔中单位体积流体的弥散增强,Taylor 空腔沿轴向速度衰减增大,使得x=34 mm,d0=2.0 mm 时的Taylor 空腔的轴向位移逐渐大于d0=1.5 mm 时的位移。从图8中还可以看出喷嘴直径较大时,Taylor 空腔前端出现“倒退”现象的时间将后移。d0分别为2.0、1.5 mm时,Taylor 空腔扩展到第2 级台阶时所用的时间分别为1.03、0.97 ms;扩展到第3 级台阶时所用的时间分别为2.55、3.50 ms。从图9 中可看出,Taylor 空腔轴向扩展速度具有波动性。
2.4 渐扩结构因子ΔD/L 对等离子体射流在液体工质中扩展特性的影响
为了观察渐扩台阶长度和直径对等离子射流扩展过程的影响,采用2 种总长一样的观察室,一个为3 级,另一个为4 级,其目的是:(1)在渐扩直径相同的条件下,选取台阶长度不同,观测Taylor 空腔扩展形态的变化;(2)在第4 级,一个台阶直径增大,另一个不变,观测Taylor 空腔扩展形态的变化。综合两者,体现了ΔD/L 这一参数变化对Taylor 空腔扩展形态的影响。图10 显示ΔD/L 分别为0.4 和0.6时,Taylor 空腔的轴向扩展位移与时间的关系曲线,其中Uc=2 600 V,d0=2.0 mm。
由图10 可见,在距离喷口20 mm 范围内,两者扩展位移几乎一样,但超过20 mm 后,ΔD/L=0.6的扩展位移比ΔD/L=0.4 的小。这是由于x=20 mm处是观察室(ΔD/L=0.6)第2 级台阶的渐扩处,渐扩边界诱导Taylor 空腔径向脉动效应,使得Taylor 空腔的径向湍动能增大,从而削弱了Taylor 空腔轴向湍动能,因此Taylor 空腔轴向位移扩展变慢,此时针对ΔD/L=0.4 的观察室,其第1 级长度为30 mm,不存在渐扩效应。渐扩结构因子ΔD/L 为0.6、0.4 时,Taylor 空腔扩展到x=30 mm 时,所用时间分别为1.04、0.97 ms,相应的瞬时速度为25.2、29.6 m/s。当x=50 mm,扩展所用时间分别为2.58、1.92 ms,相应的瞬时速度为9.55、14.09 m/s。

图9 不同喷嘴直径下的v-t 曲线Fig.9 v-t curves at different nozzle diameters
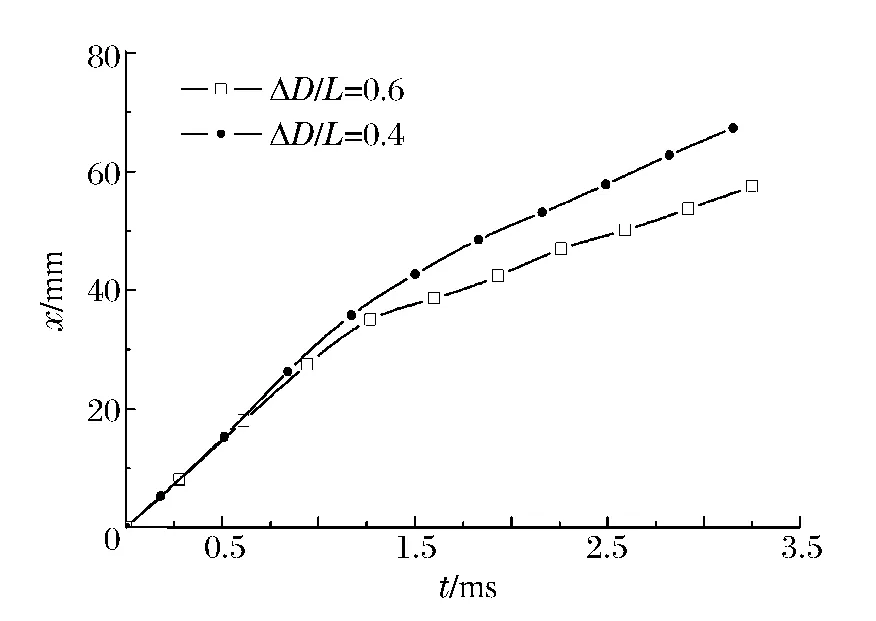
图10 不同ΔD/L 时的x-t 曲线Fig.10 v-t curves at different divergent ratios
3 结 论
在本文的实验工况下,可得出如下结论:
(1)等离子射流在圆柱渐扩边界的液体工质中扩展时,Taylor 空腔轴向速度具有波动性,总体上呈衰减趋势。由于受到台阶径向诱导作用,Taylor 空腔在渐扩处会出现回流卷吸现象。Taylor 空腔在扩展过程中,前端面可能会出现“倒退”现象。
(2)放电电压越大,Taylor 空腔的轴向扩展位移越大,轴向扩展速度也越大。
(3)喷嘴直径较大时,Taylor 空腔轴向扩展位移、扩展速度总体上相对较大。Taylor 空腔出现“倒退”的现象推迟。
(4)渐扩结构因子ΔD/L 越大,渐扩形边界对Taylor 空腔径向扰动的影响越大,Taylor 空腔轴向扩展位移的增量就越小。
[1] Kim J U,Suk H.Characterization of high-density plasma produced by electro-thermal capillary discharge[J].Applied Physics Letters,2002,80(3):368-370.
[2] Wilson D E,Kim K J,Raja R R.Theoretical analysis of an external pulsed plasma jet[J].IEEE Transaction on Magnetics,1999,35(1):228-233.
[3] Hsiao C C,Phillips G T,Su F Y.A numerical model for ETC gun interior ballistics applications[J].IEEE Transaction on Magnetics,1993,29(1):567-572.
[4] 刘东尧,周彦煌.液体发射药电热化学发射内弹道一维两相流模型及数值模拟[J].爆炸与冲击,2002,22(4):158-162.LIU Dong-yao,ZHUO Yan-huang.A 1-dimension two phase interior ballistics model of liquid propellant electrothermal chemical launching[J].Explosion and Shock Waves,2002,22(4):158-162.
[5] Kuo K K,Cheung F B,Hsieh W H.Experiments study of plasma/fluid interaction in a simulated CAP gun[C]∥Proceeding of the 27th JANNAF combustion subcommittee meeting.Maryland,USA,1990(1):365-375.
[6] Arensburg A,Wald S,Goldsmith S.X-ray diagnostics of a plasma-jet-liquid interaction in electrothermal guns[J].Journal of Applied Physics,1993,73(5):2145-2154.
[7] 周彦煌,刘东尧,余永刚.非稳态等离子体射流在液体中的膨胀特性[J].南京理工大学学报,2003,27(5):525-529.ZHUO Yan-huang,LIU Dong-yao,YU Yong-gang.Expansion characteristics of transient plasma jet in liquid[J].Journal of Nanjing University of Science and Technology,2003,27(5):525-529.
[8] Talley R L,Owczarczak J A.Investigation of bulk-loaded liquid propellant gun concepts[R].ADA279904,1994.
[9] YU Yong-gang,YAN Shan-heng,ZHAO Na,et al.Experimental study and numerical simulation on interaction of plasma jet and liquid media[C]∥Power and Energy Engineering Conference,2009:1-7.

