基于Volterra 级数的核爆地震参数化非线性特征提取方法*

韩绍卿，李夕海，伍海军，刘代志

(第二炮兵工程学院，陕西 西安710025)

地震波方法是监测核实验的重要方法［1］。分布于全球范围内的世界标准地震台网以及各个国家和地区的地震台网可以及时有效地监测到某一地区的地震事件。由地震仪获取的地震波形信号为一时间序列，该时间序列中包含了有关震源的丰富信息。地下核爆炸的自动监测问题是一个模式识别问题，解决该问题的关键在于如何对地震时间序列提取出有效的特征，将核爆炸事件同其他干扰事件(如天然地震、化学爆炸)区分开来。

在对时间序列信号的分析和特征提取中，目前常用的方法可分为两类［2-3］:一类是非参数信号表示技术，比如傅立叶变换，各种时频分析技术;另一类是参数化的信号建模技术。对于地震波时间序列的特征提取，采用的非参数化分析方法主要有:傅立叶变换［4］、短时傅立叶变换［5］、魏格纳分布［6］、小波变换［7］等;参数化信号建模则主要采用ARMA(autoregressive moving average)模型［8］。参数化核爆地震特征提取的基本思想是:首先对地震波时间序列建立ARMA 模型，然后提取模型的参数作为特征进行分类判别。对于线性时不变最小相位系统，ARMA 模型是在实际中获得广泛应用的时间序列信号模型。该模型是建立在观测信号为平稳、高斯时间序列的基础之上的。但是对于地震波信号的分析和处理来说，大地系统不是一个线性系统，时不变和最小相位特性通常是不满足的，地震波信号也并非是平稳的满足高斯分布的信号［9］。因此基于ARMA 模型的核爆地震特征的识别率不高。研究显示，地震波信号是一种非线性信号，且具有混沌特性［10-11］，所以采用非线性方法对地震波信号进行建模才更合理。Volterra 级数是一种泛函级数，大多数非线性动态系统都可以用Volterra 级数逼近到任意精确的程度［12］。

本文中，基于混沌时间序列分析中的相空间重构理论，采用Volterra 自适应预测模型对地震波时间序列进行建模，进而提取模型的参数作为地震波信号的特征进行分类识别，获得比ARMA 模型参数更好的分类效果。研究表明，地震波信号中的线性、非线性和高阶统计信息在核爆地震分类中发挥着重要作用。

1 基于模型的地震波非线性特征提取方法

提出的核爆地震非线性特征提取的核心思想是:基于地震波信号的混沌特性，对地震时间序列进行相空间重构，然后采用非线性级数Volterra 级数建立自适应预测模型，利用模型参数的信息凝聚性获得地震波信号的低维非线性特征。该方法的关键是地震波信号的相空间重构和重构相空间内Volterra 自适应预测模型的建立。

1.1 混沌时间序列的Volterra 自适应预测模型

混沌时间序列预测的基础是时间延迟相空间重构理论，假设观测到的混沌时间序列为x(n)，n=1，2，…，N，通过延迟坐标重构可获得如下的延迟坐标向量

式中:m 为嵌入维数，τ 为延迟时间。鉴于实际中大量的非线性系统都可用Volterra 级数得到很好的表征，采用Volterra 级数展开式来构造混沌时间序列的非线性预测模型［13］。设非线性离散动力系统的输入为X(n)，输出为y(n)=^x(n+1)，则该非线性系统函数的Volterra 级数展开式为

式中:hp(m1，m2，…，mp)为p 阶Volterra 核。

这种无穷级数展开式在实际应用中无法实现，必须采用有限截断和有限求和的形式。在二阶截断求和的情况下Volterra 级数展开式为

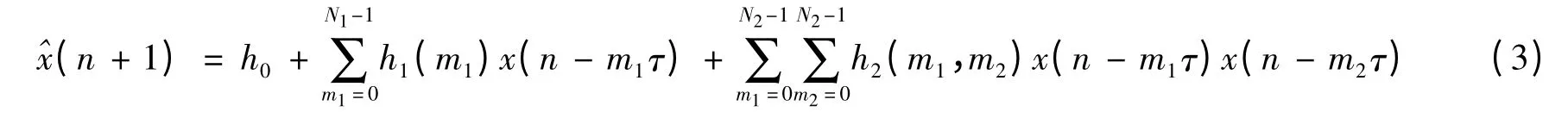
实际应用中，滤波器的长度N1、N2必须取有限长。根据Takens 嵌入定理，可将N1、N2均取为N1=N2=m。式(3)为一非线性模型，线性扩展后可用线性自适应FIR 滤波器实现。定义滤波器的输入信号矢量为

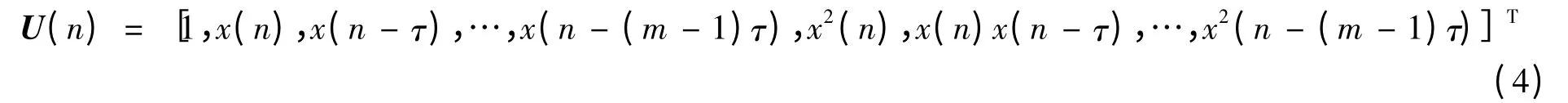
以及滤波系数矢量

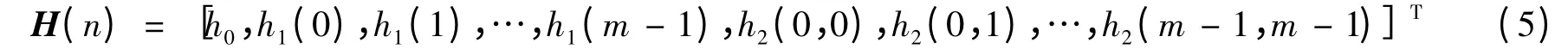
则式(3)可表示为

对于式(6)这种自适应滤波器，可采用最小均方误差自适应算法来求解。

以上简要阐述了二阶截断情况下的Volterra 自适应预测模型，同理可将其扩展到更高阶，在此不再赘述。

1.2 地震波非线性特征提取方法

核爆地震和天然地震信号是混沌信号，但其混沌参数(如分维数)不适合作模式识别的特征参数［11］。本文中则根据地震波的混沌特性，利用Volterra 级数建立地震波时间序列的自适应预测模型，在此基础上提出一种参数化的核爆地震非线性特征提取算法，该算法的流程如图1 所示。

图1 核爆地震非线性特征提取算法流程图Fig.1 Flow chart of nonlinear feature extraction algorithm of nuclear explosions and earthquakes

在特征提取过程中，非常关键的一个步骤是混沌系统参数——时间延迟和嵌入维的确定。在一般的混沌时间序列(特别是基于混沌动力学模型的时间序列)分析中，已经发展了多种估计时间延迟和嵌入维的方法。但是在核爆地震特征提取中，这些方法不太适用，原因如下:(1)不同的参数估计方法获得的参数往往不同，实践中到底该采用哪种方法尚无严格标准。(2)在进行参数估计时，大部分情况下数据量要求都比较大，而核爆炸是在瞬间完成的，一般情况下，天然地震的持续时间也不会很长，再加上地震仪器采样率的限制，实际中获得地震波信号长度都很有限。(3)实际中获得的地震波信号都会受到噪声的污染，但很多情况下对噪声的统计分布和强度情况了解较少，此外，即使获得了噪声的先验信息，但降噪会给原动力系统的信息造成损失。(4)核爆地震的分类必然涉及大量的样本，即使是同类样本之间的混沌参数也会有一定的差异。特征提取的目的在于找到同类样本的共性和不同类样本的差异，而没有必要一定要获得对于每个单个样本最佳的混沌参数。此外，样本的混沌参数不同会造成样本特征空间维数的不同，给后续样本的分类带来很大麻烦。这正是模式识别过程中特征提取与一般信号分析的不同点。为解决这一问题，采用如下的方法:首先采用自相关和去偏复自相关法确定每一个地震波样本的时间延迟，经过综合分析得出地震波样本的时间延迟的分布范围，采用Grassberger 和Procaccia 提出的G-P 法和Cao 氏法确定每一个地震波样本的嵌入维，经过综合分析得出地震波样本的嵌入维的分布范围，然后再将二者的取值范围适当增大，在增大的取值范围内对所有的核爆和地震样本都分别采用相同的时间延迟和相同的嵌入维进行自适应预测建模，最后进行特征提取和分类判别，根据识别率确定最佳的时间延迟和嵌入维。这样处理的依据和好处是:(1)Takens 定理表明，只要相空间嵌入维大于饱和嵌入维时，都可以得到原动力系统的重构。此外定理中嵌入维应当满足的条件只是一个充分条件，而不是必要条件，并不能排除在比这一要求更小的嵌入维时得到较好的重构。这说明满足重构的嵌入维是在一个范围内变化的。(2)延迟时间的确定以相关性为准则，希望相邻点间既不能不相关，又不能相关性太强。这种矛盾表明延迟时间也是在一定范围内满足要求。(3)现有计算方法获得的时间延迟和嵌入维相对于相空间重构来说是最佳的，但对于特征提取和分类而言不一定最佳。而本文中提出的在一定范围内经过比较后获得最佳时间延迟和嵌入维，其判别标准是识别率，这样能保证获得对于分类而言最佳的参数。

地震台站获得的地震波信号是震源(爆炸、地震)发出的地震波经过大地系统多次滤波后产生的时间序列。由于震源激发地震波的过程本身是一个非线性过程，且大地系统是一个非线性系统，因此地震波信号是非线性信号。有关震源的丰富信息蕴含在地震波时间序列中，当建立地震波时间序列的非线性模型之后，震源信息也同样蕴含在模型参数之中。参数模型的一个最大特点是信息的凝聚性，即大量数据所蕴含的信息凝聚成少数几个模型参数。而特征提取的目的之一也是为了实现信息的凝聚，从而能够使分类判决在维数较低的空间进行。这是本文中提出的参数化非线性特征提取方法的理论依据。

2 实验结果

实验所用的数据库为北京、兰州、恩施、昆明、琼中、上海、乌鲁木齐、海拉尔、牡丹江等9 个中周期地震台站所采集的核爆炸和天然地震所产生的地震波数据，各有54 个样本，样本的采样率为20 Hz。为了计算方便和便于对比，对每个样本从地震波初至点开始截取1 024 个数据点。图2 给出了一次典型的核爆炸样本和一次典型的天然地震样本的时域波形图。可以看出，对于典型的核爆炸和天然地震，二者时域波形有较为显著的差异。但是通过对数据库中样本的统计分析发现，并非所有的核爆炸样本和天然地震样本之间都具有这样的差异。因此必须通过特征提取，将核爆炸和天然地震之间的差异量化。此外，不同样本的幅度有很大差异。造成这种差异的主要原因是:不同的地震事件震级不同;不同的地震事件距离接收台站的距离不同。为了消除波形幅度对判据的影响，特征提取算法中首先需要对数据进行归一化处理。

图2 核爆炸和天然地震产生的地震波形Fig.2 Seismic waveforms from nuclear explosion and natural earthquakes

根据图1 中的特征提取算法流程图我们进行了核爆地震非线性特征提取实验。在验证特征的有效性时，采用k-近邻分类器进行分类实验，其中错误识别率采用留一法获得。在对地震波时间序列进行建模时，需要确定的参数为Volterra 级数的阶数p、相空间重构的时间延迟τ 以及滤波器长度(即嵌入维数m)。随着阶数p 的增加，Volterra 级数滤波器系数的个数迅速增加，导致计算量飞速增长。因此仅在Volterra 级数的阶数p=2，3 时展开研究。对于时间延迟τ，经过综合分析得到的取值范围为［2，8］，其中在τ 取6 时获得最佳的识别效果。对于嵌入维数m，经过综合分析得到的取值范围为［2，11］。为了考察滤波器长度对特征有效性的影响，同时也为了与已有的ARMA 模型参数特征进行比较，在τ=6、嵌入维m 取值范围为［2，11］的情况下进行特征提取和分类判别实验。从形式上看，本文中采用的Volterra 级数模型为自回归模型，因此将ARMA 模型中的自回归模型(AR 模型)参数特征作为比较的对象，其中AR 模型的阶数取值范围同样为［2，11］。

不同模型参数特征的分类结果如图3 所示。为了便于分析和对比，将AR 模型参数特征和Volterra自适应预测模型参数特征的分类识别结果画在同一张图中。图中纵坐标E 代表错误识别率。需要注意的是，对于AR 模型，图中的横坐标代表的是不同的阶数(用l 表示)，而对于Volterra 自适应预测模型，横坐标代表的是不同的嵌入维。从图中可以看出，AR 模型参数特征识别效果不太理想，在p=3 时达到最低错误识别率，在0.3 左右，并且并非阶数越高识别效果越好。对于本文提出的非线性模型参数特征，在p=2 时，除嵌入维m=2，5 的情况外，其错误识别率都低于AR 模型参数特征的最低错误识别率，在m=9 时达到最低错误识别率，为0.213。在p=3 时，非线性模型参数特征在所有嵌入维情况下的错误识别率都低于AR 模型参数特征的最低错误识别率，并且在m=7 时达到最低错误识别率，为0.194 4。总体来看，本文中提出的非线性模型参数特征优于线性模型的AR 模型参数特征。在非线性模型参数特征中，与阶数为2 情况下获得的特征相比，p=3 情况下获得的特征识别效果更好，且对于嵌入维数更加不敏感。

图3 不同特征提取方法的分类性能比较Fig.3 Classification performance comparison for different feature extraction methods

3 结果分析

由实验结果可以看出，本文中提出的非线性模型参数特征的分类效果好于现有的线性AR 模型参数特征的分类效果，根本原因在于Volterra 自适应预测模型很好地刻画了地震时间序列非线性本质特征以及所具有的混沌特性。具体原因可有如下几点:(1)地震时间序列本质上是非线性的，AR 模型只利用了地震波的线性因素，而Volterra 自适应预测模型综合利用了线性和非线性因素。(2)地震时间序列是非平稳的时间序列，用于刻画非平稳时间序列的模型参数应该是时变的。AR 模型参数是固定不变的，而Volterra 自适应预测模型能够根据地震波统计特性的改变而自适应地调整模型参数，因此后者对地震波的逼近精度更高。(3)AR 模型只利用了地震波的二阶统计信息，而Volterra 自适应预测模型充分利用了地震波的高阶统计信息。高阶统计信息在核爆地震分类中是有用的，三阶Volterra 自适应预测模型参数特征优于二阶Volterra 自适应预测模型参数特征也充分说明了这一点。

4 结 论

由于地震时间序列为非线性时间序列，因此需要采用非线性模型对其进行准确描述。利用地震时间序列的混沌特性，先进行相空间重构，然后在重构的相空间内建立地震波的Volterra 自适应预测模型，进而提取模型的参数作为核爆炸和天然地震的特征进行分类实验，获得了较好的分类效果。通过研究获得的主要结论为:基于Volterra 级数的非线性模型参数特征优于现有的线性AR 模型参数特征;在非线性模型参数特征中，三阶Volterra 级数自适应预测模型参数特征优于二阶Volterra 级数自适应预测模型参数特征。因此，在核爆地震特征提取中，充分考虑和应用地震时间序列的非线性和高阶统计信息将有助于获得更有效的特征。

［1］ Hafemeister D.Progress in CTBT monitoring since its 1999 senate defeat［J］.Science and Global Security，2007，15:151-183.

［2］ Sakkalis V，Cassar T，Zervakis M，et al.Parametric and nonparametric EEG analysis for the evaluation of EEG activity in young children with controlled epilepsy［J］.Computational Intelligence and Neuroscience，2008，doi:10.1155/2008/462593.

［3］ Carden E P，Brownjohn J M W.ARMA modelled time-series classification for structural health monitoring of civil infrastructure［J］.Mechanical Systems and Signal Processing，2008，22(2):295-314.

［4］ 李夕海，刘刚，刘代志，等.基于最近邻支撑向量特征线融合算法的核爆地震识别［J］.地球物理学报，2009，52(7):1816-1824.LI Xi-hai，LIU Gang，LIU Dai-zhi，et al.Discrimination of nuclear explosions and earthquakes using the nearest support vector feature line fusion classification algorithm［J］.Chinese Journal of Geophysics，2009，52(7):1816-1824.

［5］ Arrowsmith M D，Arrowsmith S J，Stump B W，et al.A suite of discriminants for ground-truth mining events in the western US and its implications for discrimination capability in Russia［C］∥Proceedings of 2008 Monitoring Research Review:Ground-Based Nuclear Explosion Monitoring Technologies.Portsmouth，Virginia，USA，2008:544-553.

［6］ Benbrahim M，Benjelloun K，Ibenbrahim A，et al.A new approaches for seismic signals discrimination［J］.Proceedings of World Academy of Science，Engineering and Technology，2007，21:183-186.

［7］ Piotr F，Hernando O.Consistent classification of non-stationary time series using stochastic wavelet representations［J］.Journal of the American Statistical Association，2009，104(485):299-312.

［8］ Cercone J A，Foster V S，Clark W M.Application of neural networks to seismic signal discrimination research findings［R］.PL-TR-94-2122，1994.

［9］ 邢贞贞，韩立国，王宇，等.高阶统计量方法在地震信号分析中的应用［J］.吉林大学学报(地球科学版)，2007，37 增刊:139-142.XING Zhen-zhen，HAN Li-guo，WANG Yu，et al.Application of higher-order statistics in seismic signal analysis［J］.Journal of Jilin University(Earth Science Edition)，2007，37 suppl:139-142.

［10］ Liu D，Red S，Wei Y，et al.Attractor analysis and its applications to seismic pattern recognition of nuclear explosion［C］∥3rd International Conference on Signal Processing.Beijing，China，1996:1324-1329.

［11］ 刘代志，邹红星，韦荫康，等.分形分析与核爆地震模式识别［J］.模式识别与人工智能，1997，10(2):153-158.LIU Dai-zhi，ZOU Hong-xing，WEI Yin-kang，et al.Fractal analysis with applications to seismic pattern recognition of nuclear explosion［J］.Pattern Recognition and Artificial Intelligence，1997，10(2):153-158.

［12］ Kalli R R.Nonlinear modeling of radio frequency circuits to estimate third-order nonlinear distortions［D］.Florida:Florida International University，2008.

［13］ 许小可.海杂波的非线性分析与建模［D］.大连:大连海事大学，2007.