分层递变梯度蜂窝材料的面内冲击性能*

刘 颖，何章权，吴鹤翔，张新春

(北京交通大学土木建筑工程学院力学系，北京100044)

多孔材料由于具有微结构弹塑性屈曲和脆性断裂为特征的平台变形特性，因而成为一种理想的吸能材料，近年来广泛应用于能量吸收器的设计中［1-2］。但是需要指出的是，在冲击载荷作用下，多孔材料的动力响应往往伴随着一个很大的初始应力峰值，这对多孔材料的能量吸收是不利的。因此，降低初始应力峰值，提高和控制平台区能量吸收能力在多孔材料能量的设计中十分重要。

作为一种简单的能量吸收结构，环状蜂窝材料被广泛应用于各种能量吸收结构中［3］。V.P.W.Shim 等［4］研究了正方形和六边形排布圆管的面内冲击性能，L.L.Hu 等［5］、D.Karagiozova 等［6-7］对圆环蜂窝材料的变形特征进行了大量研究，结果表明，圆环的几何尺寸(壁厚和半径)对其响应具有决定性的作用。对于相同的壁厚，小的圆环半径对应着更高的平台应力，但是初始应力峰值也大幅增加，而应力平台长度则减小。虽然增大圆环半径可以降低初始应力峰值并延长平台长度，但平台应力值也会降低。因此在使用均匀蜂窝材料时，很难实现多目标优化。目前，基于梯度材料的概念，在多孔材料静力学性能控制方面进行了一些尝试以提高其能量吸收率［8］、弹性模量和屈服强度［9］、断裂强度［10］等，但对于其动力学性能控制的研究还没有充分展开。

本文中，借鉴功能梯度材料的概念，建立分层递变梯度多孔圆环蜂窝模型(functionally layered circular honeycombs，FLCHs)。通过改变胞元半径，使承载能力变成一个可控的空间变量而不再是一个恒定值，为实现蜂窝材料的多目标优化设计提供可能。通过数值计算讨论在不同冲击速度下梯度系数和圆环排布方式对蜂窝材料冲击动力学响应特性的影响。计算结果表明，通过适当选取梯度系数和排布方式，可以有效控制能量吸收过程，并降低初始应力峰值。

1 计算模型

图1 给出了分层递变梯度蜂窝材料的结构示意图。蜂窝材料分为3 部分，每一部分被壁厚相同但半径不同的圆环按正方形(或六边形)排布填充。圆环之间通过接触点连接。不同层圆环半径由线性函数控制，即

式中:αi为梯度系数，yi0是不同分层中第1 层圆环中心(相对冲击端的位置)距冲击端第1 层圆环中心(y=0)的距离，L2是试件的初始长度，R0是靠近冲击端第1 层圆环的半径，R 为当前层圆环的半径。当α＜0 时，不同层圆环半径逐渐减小(见图1(a));而当α ＞0 时，不同层圆环半径逐渐增加(见图1(b))。梯度系数的绝对值越大，圆环半径变化越剧烈(图中RL、RM和RS分别表示不同部分圆环的半径)。当然，也可以通过改变圆环壁厚来控制蜂窝材料的面内性能。需要指出的是，材料分成几层，每层圆环数量多少都不是绝对的，可以根据实际使用要求进行设计。

为了讨论梯度系数的变化对响应特性的影响，针对某一特定排布结构，分别从不同端进行冲击(即调整梯度系数)。不同层圆环半径分别为RL=5 mm，RM=3.3 mm，RS=2.2 mm。因此对于正方形排布蜂窝材料，当α ＞0 时，从RS到RM，RM到RL的梯度系数分别为α1=1.4 和α2=1.79;当α ＜0 时，从RL到RM，RM到RS的梯度系数为α1=-1.12 和α2=-0.87。对于六边形排布蜂窝材料，当α ＞0 时，梯度系数分别为α1=1.48 和α2=1.79;而当α ＜0 时，梯度系数为α1=-1.11 和α2=-0.87。

图1 分层递变梯度多孔圆环蜂窝模型Fig.1 Functionally layered circular honeycombs

分层梯度圆环蜂窝材料的面内冲击计算模型如图2 所示。刚性板以恒定速度沿y 方向运动，底端刚性板固定。蜂窝材料左右两侧为自由端。另外，结构所有面外位移均被限制以保证平面应变状态。基体材料为金属铝，采用理想弹塑性模型，杨氏模量E=69 GPa，屈服应力σy=76 MPa，泊松比ν =0.3，密度ρ=2.7 t/m3。应用非线性有限元软件ABAQUS/EXPLICIT 进行蜂窝材料的冲击动力学特性计算，计算中选用S4R 单元(4 节点减缩积分的壳单元)。为了收敛和计算精度的需要，沿壳厚度方向定义5 个积分点。在压缩过程中所有可能接触的表面定义为自由接触表面。另外，刚性板与蜂窝试件的外表面均视为光滑，两者接触无摩擦。

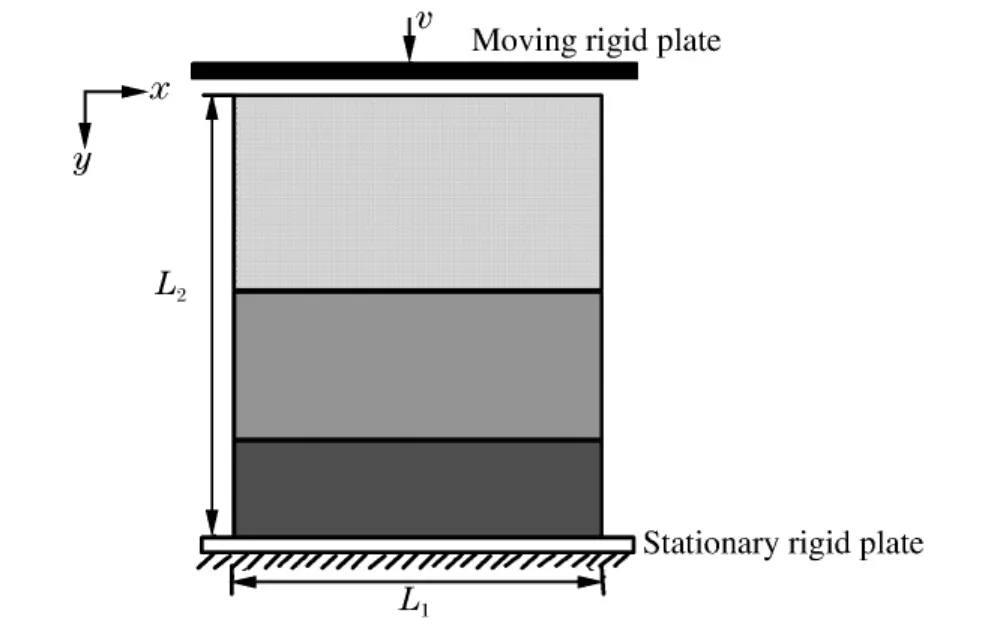
图2 分层梯度蜂窝材料的面内冲击加载示意图Fig.2 Calculating model for FLCHs

计算中不同层圆环的数目为:nx，L×ny，L=8×3，nx，M×ny，M=12×5，nx，S×ny，S=18×7。正方形和六边形排布圆环蜂窝材料的尺寸分别为和L1×L2计算中圆环厚度t=0.2 mm。分层蜂窝材料的相对密度为

式中:ρh是蜂窝材料的密度，ρs是基体材料的密度，N 是圆环的总数，Ri是第i 个圆环的半径。根据方程(2)，分层蜂窝材料的相对密度分别为

式中:S 表示胞元正方形排布，H 表示胞元六边形排布。

2 计算结果和讨论

2.1 正方形排布分层蜂窝材料的动力响应

图3(a)、(b)分别给出了梯度系数α ＜0 和α ＞0，相对压缩量为0.1、0.3 和0.5 时分层递变梯度蜂窝材料的变形模式。冲击速度的选取根据RL填充均匀蜂窝材料的临界速度确定(陷波波速vw=7.3 m/s;冲击波速vs=62.2 m/s)［11-12］。从图3(a)中可以看出，当α ＜0 时，蜂窝材料表现为从冲击端大圆(半径RL)到固定端小圆(半径RS)的逐层压缩模式。但当α ＞0 时，在低速冲击作用下(v=7 m/s＜vw)，局部变形带从试件底端大圆启动，随着相对压缩量的增加，表现为从RL到RM再到RS的逐层顺序压缩。随着冲击速度的增加(vw＜v=14 m/s ＜vs)，局部变形带在RS段启动，随着相对压缩量的增加，RM段和RL段开始变形且以RM段变形为主，最后表现为RS段的压缩。而随着冲击速度的进一步增加(v=70 m/s ＞vs)，惯性效应增强，则对应着从冲击端小圆(半径RS)到固定端大圆(半径RL)的逐层压溃变形模式。另外，当α ＜0 时，胞元排布方式的变化对其变形模式的影响较小。但当α ＞0 时，胞元的排布对变形带的启动有所影响。在中低速冲击作用下，六边形排布蜂窝材料局部变形带在不同层交界面处的启动更加明显。

图3 不同冲击速度下分层梯度蜂窝材料变形模式Fig.3 Deformation modes for FLCHs at different impact velocities

图4 给出了分层递变梯度蜂窝材料冲击端名义应力和应变曲线。其中名义应力定义为刚性板压缩反力和试件初始横截面的比值;名义应变为试件沿y 方向的变形量和结构初始长度之比。从图中可以看出，由于不同半径圆环对应的临界破坏力不同［12］，分层递变蜂窝材料各层的逐次变形使得材料响应表现出分段特性。半径越大，相应的分段平台应力值越低。分段平台的长度可根据不同层的厚度相对于结构沿y 方向的长度的比值与试件相对密度的乘积来确定。而不同平台段的应力值满足

图4 不同冲击速度下分层梯度蜂窝材料冲击端的名义应力应变曲线Fig.4 Nominal stress-strain curves for the impact end of FLCHs at different impact velocities

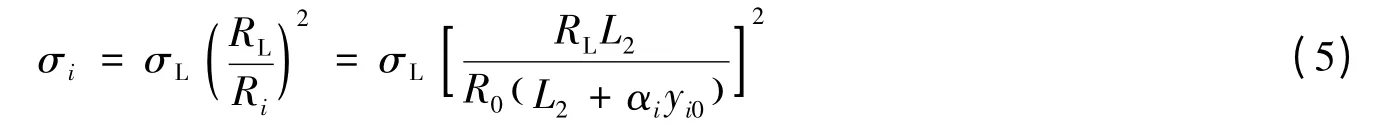
式中:σL为大圆RL填充均匀蜂窝材料的平台应力值，下标i 表示对应于不同层的分段平台应力值。

从图4 中可以看出，对于α ＞0 或α ＜0 的分层梯度蜂窝材料，其动态响应在低速冲击荷载作用(v=7 m/s)下基本相同，试件响应为逐渐增加的3 个平台阶段(见图4(a))。随着冲击速度的增加，与α＜0 的情况不同，当α ＞0 时，由于其局部变形带从小圆RS启动(图3(b)中v=70 m/s 时)，因此在初始压缩阶段对应着一个较高的平台段(见图4(b)、(c))。而对于α ＜0 的分层蜂窝材料，其初始应力峰值则被大大减小。另外，对于六边形排布蜂窝材料其动力响应的分段特性更加明显。

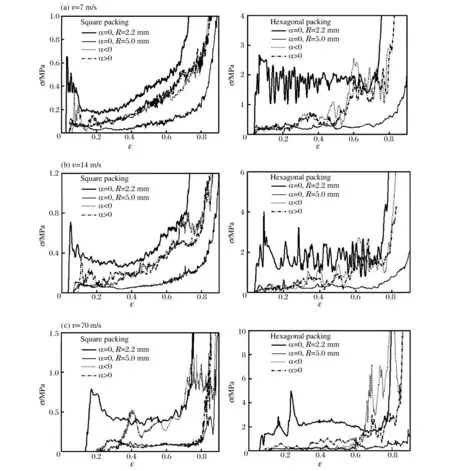
图5 不同冲击速度下分层梯度蜂窝材料固定端的应力应变曲线Fig.5 Nominal stress-strain curves for the distal end of FLCHs at different impact velocities

图5 给出了分层递变蜂窝材料固定端的动力响应。从图中可以看出，远端的响应较冲击端滞后，且冲击速度越高，滞后性越明显。随着冲击速度的提高，当α＞0 时，远端的应力水平大大降低，和大圆填充均匀蜂窝材料的响应趋于一致。而对于α ＜0 的情况，其初始应力峰值虽大大降低，但随着压缩量的增加，其响应和小圆填充均匀蜂窝材料趋于一致。可见，对于α ＞0 分层蜂窝材料可以大大降低传入被保护结构的应力值水平。而正方形排布蜂窝材料相对六边形排布蜂窝材料更加明显。

2.2 分层蜂窝材料的能量吸收特性

图6 给出了不同分层蜂窝材料单位质量的能量吸收和相对压缩量之间的关系。其中Em为材料单位质量吸收的能量［13］，即

从图6 中可以看出，六边形排布蜂窝材料单位质量的能量吸收率高于正方形排布蜂窝材料。对于正方形排布蜂窝材料，在中低速(v 在vw附近变化)冲击时，对于某一特定结构，冲击方向对其单位质量的能量吸收率影响不大。但对于六边形排布蜂窝材料，冲击端的变化，即梯度系数符号的变化，对其单位质量能量的吸收有一定影响。当α ＜0 时，单位质量吸收的能量增加。随着冲击速度的增加，α ＞0的分层蜂窝材料表现为前程吸能。如图6(c)所示，对于六边形蜂窝材料，当压缩应变为0.4 时，已经吸收了近60%的能量。但α ＜0 的分层蜂窝材料表现为后程吸能。这样，通过控制梯度系数的变化即可调控材料的能量吸收过程。

3 结 论

分层梯度蜂窝材料的动力响应表现出分段特性。通过控制胞元半径的变化范围，可以控制材料的平台应力变化范围。在冲击端排布较大的圆环可以有效降低初始应力峰值。通过调整梯度系数，可以控制胞元的能量吸收特性。当α ＞0 时，分层蜂窝材料以前程吸能为主;当α ＜0 时，以后程吸能为主。另外，α ＞0 的分层排布蜂窝材料可以有效降低传入被保护结构的应力值水平，而正方形排布效果更显著。因此通过适当选择胞元半径、胞元排布方式和梯度系数可以有效控制材料的能量吸收性能。

图6 不同排布分层梯度蜂窝材料能量吸收特性比较图Fig.6 Energy absorption per mass for FLCHs with different gradient coefficients

［1］ Evans A G，Hutchinson J W，Ashby M F.Multifunctionality of cellular metal systems［J］.Process in Materials Science，1998，43(3):171-221.

［2］ Gibson L J，Ashby M F.Cellular solids:Structure and properties［M］.Cambridge:Cambridge University Press，1997.

［3］ Carney ⅢJ F.Motorway impact attenuation devices:Past，present and future［C］∥Jones N，Wierzbicki T.Structural Crashworthiness and Failure.London＆New York，1993:423-466.

［4］ Shim V P W，Stronge W J.Lateral crushing in tightly packed arrays of thin-walled metal tubes［J］.International Journal of Mechanical Sciences，1986，28(10):709-728.

［5］ Hu L L，Yu T X，Gao Z Y，et al.The inhomogeneous deformation of polycarbonate circular honeycombs under in-plane compression［J］.International Journal of Mechanical Sciences，2008，50(7):1224-1236.

［6］ Karagiozova D，Yu T X.Post-collapse characteristics of ductile circular honeycombs under in-plane compression［J］.International Journal of Mechanical Sciences，2005，47(4/5):570-602.

［7］ Karagiozova D，Yu T X.Strain localization in circular honeycombs under in-plane biaxial quasi-static and low-velocity impact loading［J］.International Journal of Impact Engineering，2008，35(8):753-770.

［8］ Liang C，Kiernan S，Gilchrist M D.Designing the energy absorption capacity of functionally graded foam materials［J］.Materials Science and Engineering:A，2009，507(1/2):215-225.

［9］ Ajdari A，Canavan P，Nayeb-Hashemi H，et al.Mechanical properties of functionally graded 2-D cellular structures:A finite element simulation［J］.Materials Science and Engineering:A，2009，499(1/2):434-439.

［10］ Lee S J，Wang J Q，Sankar B V.A micromechanical model for predicting the fracture toughness of functionally graded foams［J］.International Journal of Solids and Structures，2007，44(11/12):4053-4067.

［11］ Tan P J，Reid S R，Harrigan J J，et al.Dynamic compressive strength properties of aluminium foams.Part II-Shock theory and comparison with experimental data and numerical models［J］.Journal of the Mechanics and Physics of Solids，2005，53(10):2206-2230.

［12］ Hönig A，Stronge W J.In-plane dynamic crushing of honeycomb.Part I:Crush band initiation and wave trapping［J］.International Journal of Mechanical Sciences，2002，44(8):1665-1696.

［13］ Kooistra G W，Deshpande V S，Wadley H N G.Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminum［J］.Acta Materialia，2004，52(14):4229-4237.