基于分数阶Fourier 变换的远程水声通信技术研究

陈韵，王逸林，蔡平，殷敬伟，梅继丹

(哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨150001)

0 引言

1 分数阶Fourier 变换理论

分数阶Fourier 变换可以认为是一种广义的Fourier 变换。如果将普通意义上的Fourier 变换看成是时间轴旋转π/2 到频率轴，那么，分数阶Fourier 就可以认为是由时间轴旋转任意角度到分数阶域(u 域)，建立时域与分数阶域的联系。分数阶Fourier 变换的定义式写为

其中，Kp(t，u)为分数阶Fourier 变换的核函数，定义:

式中:α=pπ/2，p 为分数阶Fourier 变换的阶数，Fp表示分数阶Fourier 变换算子，因此可进一步将(1)式表示为

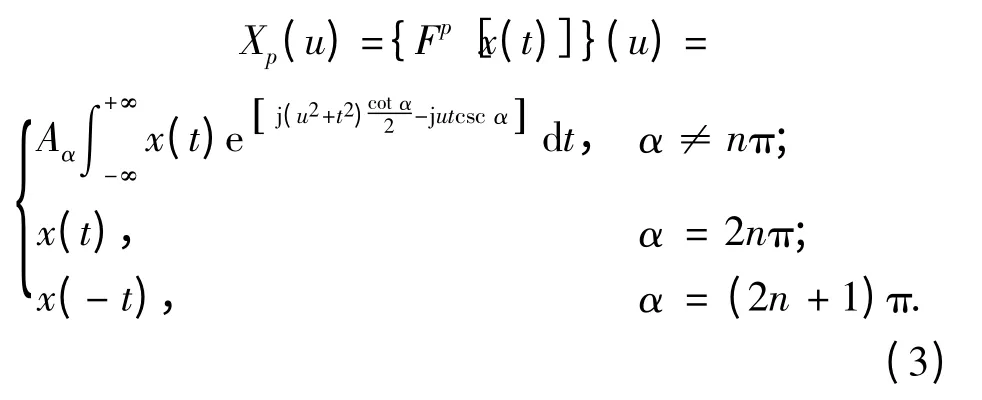
式中Aα=［(1-jcotα)/2π］0.5，从分数阶Fourier 变换的表达式可以看出，分数阶Fourier 变换的实质是角度为α 的时频面旋转。这个性质建立起分数阶Fourier 变换与时频分布的直接联系，是一种广义的Fourier 变换［3］。其旋转角度α 与线性调频信号的斜率k 满足关系

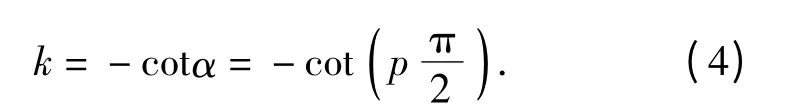
由分数阶Fourier 变换的旋转性不难推得p 阶分数阶Fourier 反变换就是做-p 阶的分数阶Fourier 变换，即

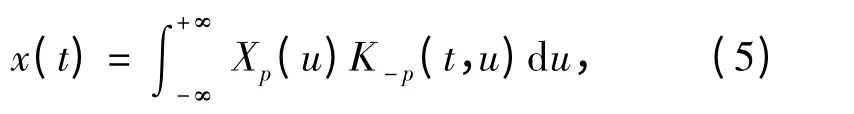
(5)式同时也反映了这样一个事实，分数阶Fourier变换也可以理解成为chirp 基分解，x(t)可以由一组正交的基函数K-p(t，u)乘以对应的权系数Xp(u)来表征，而这些基函数就是线性调频的复指数函数［5］。

伴有颈动脉斑块的急性缺血性卒中患者急性期血清学相关指标水平的研究 …………………………………………………………… 梁志刚，孙旭文，杨绍婉，等 425

文献［6-10］阐述了离散分数阶Fourier 变换(DFRFT)的具体实现方法，这些方法主要分为3 种类型:1)特征分解型;2)离散采样型;3)线性组合型。本文主要采用Ozaktas 在文献［8］中提出的对离散采样型改进的分解型算法，将分数阶Fourier 变换分解为两次chirp 信号乘法和一次chirp 信号卷积，这样就可以利用FFT 算法进行实现。

2 基于FRFT 的水声通信系统设计

前文述及，对于确定调频斜率k 的LFM 信号，其相应p 阶的分数阶Fourier 变换为u 域上的冲击函数，k 与p 满足(4)式的关系。若存在这样的时域信号集合xn(t)，使得

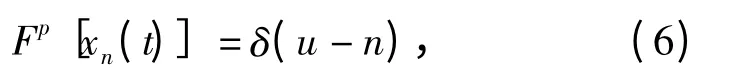
也即存在相同斜率的LFM 信号的FRFT 只是冲击函数在变换域的平移。那么便可以利用这样的信号集合作为码元集合，将要传输的信息调制到码元信号的变换域之中。文献［11］推导了这样的信号集合xn(t)，给出

式中:T 为码元宽度;α 为分数阶Fourier 变换的角度;(7)式中码元信号xn(t)具有LFM 信号的形式，只是有相位和幅值的调整。进一步说，具有相同的调频斜率和频带间隔的LFM 信号码元集合，其分数阶Fourier 变换是一系列具有固定间隔的δ 函数，间隔距离是sinα/T，这就为基于FRFT 的编解码方式打下基础。而采用相同调频斜率的LFM 信号的原因是解码时分数阶Fourier 变换的阶次保持固定不变，无需在时频面搜索峰值，从而节省大量的计算时间，使得实时通信成为可能。例如，相同调频斜率的LFM 信号x1(t)和x2(t)，中心频率分别为3 kHz 和6 kHz，其阶次p=1.010 6 的分数阶Fourier 变换如图1(a)所示。从时频分布的角度看，噪声是分布在整个时频面上，时频面旋转任何角度，即做任何阶次分数阶Fourier 变换，都不会出现能量的聚集出现峰值;但是LFM 信号在时频面有固定的分布，在相应的阶次就会出现能量聚集，这就使分数阶Fourier 变换具有良好的稳健性，抗噪声能力强，可以在信噪比很低的环境下工作。如前例中信号x1(t)在0 dB 信噪比下的分数阶Fourier 变换如图1(b)所示。

经典的脉冲位置调制(PPM)方式，并不是将要传输的信息调制在码元信号的波形中，而是将信息调制到码元出现在时间窗的位置信息中［12］。借用PPM 调制思想，基于FRFT 的水声通信编码就是将信息调制到码元变换域出现峰值的位置信息中，并且码元所能够携带信息bit 数由码元集合决定。若码元集合ST 中有码元数N，则集合ST 中N 码元可以对应分数阶Fourier 变换域携带bit 信息量n=log2N.例如，产生码元集合ST 中有16 个码元，则每个码元可携带信息的比特数为4 bit.由(7)式可以发现，对于一个码元集合中码元分割取决于码元宽度T 的选取，T 选取的越大，码元集合中码元越多，则每个码元携带信息比特数越多，但是降低通信的符号速率;反之则每个码元携带信息量少，但增加了通信的符号速率。可以用(8)式来描述通信速率

式中:N 与T 成反比关系，N=β/T.

整体通信体制如框图2所示，首先将整体通信频段作频带分割，划分为Ⅰ、Ⅱ两路子通信频带。每路子通信频带内按(7)式生成一个码元集合，作码元分割;根据输入的串行比特流串并转换、映射选择码元。在射频端将两路码元信号叠加发射，这样可以使通信速率相对于单通信信道加倍。接收端经过相应阶次的分数阶Fourier 变换之后，得到u 域中2个互不干扰的峰值位置，并且通过这2 个“脉位”可以得到发送端的码元信号，由码元反映射关系即可解出发送端所调制的比特信息。

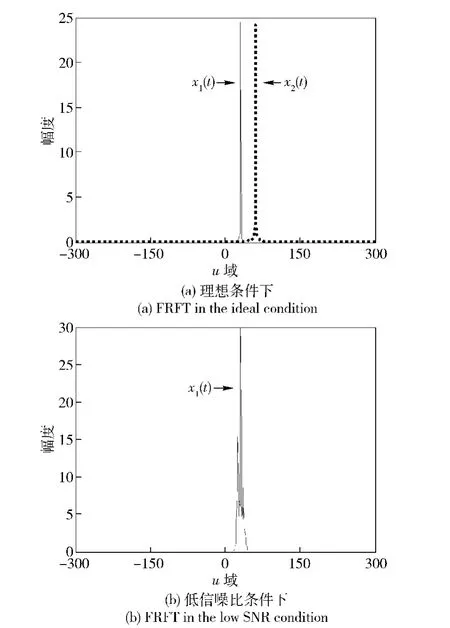
图1 相同斜率不同频带码元信号的分数阶Fourier 变换Fig.1 FRFT of the same slope code element signal with different frequency bands

3 基于Rake 接收机的多途干扰抑制

实验证明水声通信信道可被看作是缓慢时变的相干多途信道，在相干时间以内，可以近似用线性、时不变的滤波器描述［1］。冲击响应函数可表示为

式中:τi是第i 条路径信号到达的时延量;Ai是第i条路径的幅度。那么，发射信号s(t)经过水声信道在接收端的接收信号r(t)可以表示为

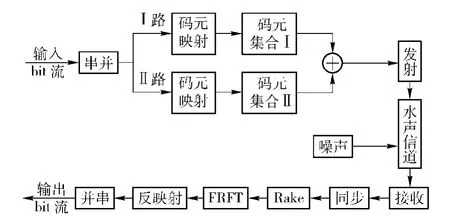
图2 FRFT-PPM 水声通信系统设计框图Fig.2 Block diagram of FRFT-PPM UWA communication system

根据分数阶Fourier 变换的线性特性及时移特性可得

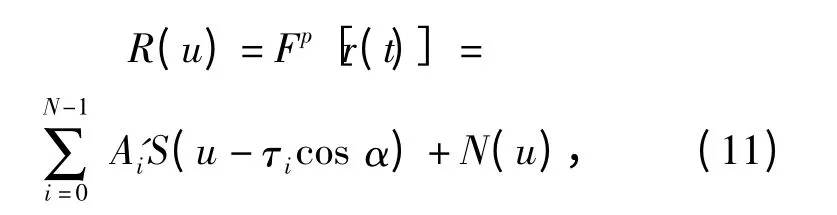
式中A'i=exp(jπτ2isinαcosα)exp(-j2πuτisinα)Ai，(11)式说明发射信号经过水声信道受多途效应影响的结果是多途分量在分数阶Fourier 变换域上峰值的移动，形成一系列“伪峰”;峰值移动的距离与多途时延分量有关，并且有幅值与相位的改变。这种多途信道对信号的影响成为码内干扰和码间干扰的最主要因素。

根据分数阶Fourier 变换的卷积性质［13］，也可以将经过多途信道的接收信号表示成

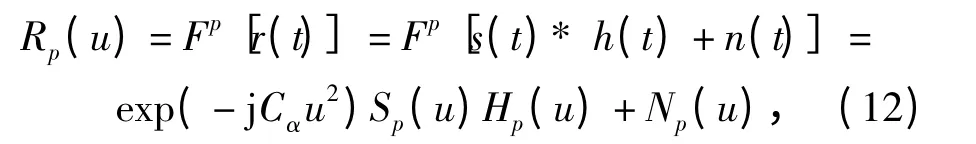
式中:Cα=(cotα)/2;Hp(u)为信道冲击响应函数h(t)的P 阶分数阶Fourier 变换:

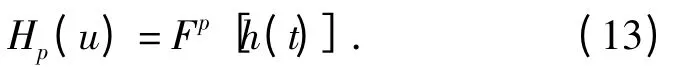
若信道冲击响应函数h(t)具有δ 函数的形式，即h(t)=δ(t)，则有

将(14)式代入到(12)式中可得

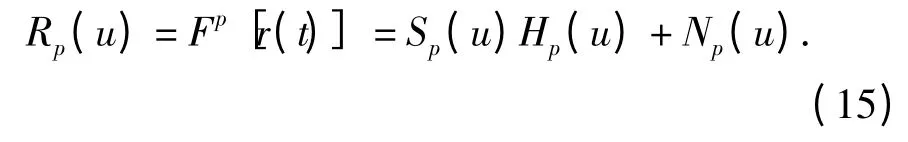
从(15)式中可以看出，如果信道冲击响应函数具有δ 函数的形式，就可以完全抑制由信道多途效应所引起的码内干扰和码间干扰，这也是目前多种信道均衡方法所追求的目标。然而，在实际应用中常常采用使信道冲击响应函数逼近δ 函数的形式去除多径信道的影响，下面将详细介绍通过Rake 接收机来抑制多途干扰的方法。

当通信信道出现深度衰落的时候，接收信号会出现很大的衰减，因而会造成误码;如果能够提供独立的衰落路径，就可以采用分集接收的技术来降低误码率［14］。一般的分集技术有频率分集、时间分集和空间分集。Rake 接收是一种特殊的分集，是当信道相干带宽远大于信号带宽时的一种分集方式。假设信号带宽为W，信道的最大延迟为τmax，则信道的可分辨独立衰落路径有L=τmax/(1/W)条。Rake 接收就是将这L 条独立信道的能量集中起来，以达到接收端有最大的信噪比，这种分集方式又被称为多径分集。实际上，Rake 接收就是将多径混叠信号根据独立多径的多径时延作时延相加，即通过修正每条多径所附加的相移来使得信号作同相相加，而噪声非同相相加，从而达到提高信噪比的目的。

从另一方面来看，对接收信号作延时相加，可以近似认为将接收信号与时反的信道冲击响应函数h(-t)作卷积，那么接收信号r(t)经过Rake 接收之后可写为

将(10)式代入(16)式中可得

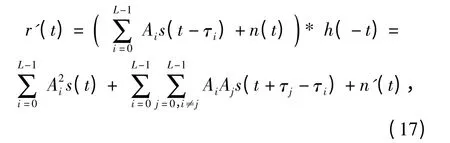
其中L 为可分辨独立衰落路径条数，将(17)式右边第1 项作为信号，第2 项和第3 项合并看作干扰，则可以认为Rake 接收机修正了多径信道给信号带来的附加相移，使得信号能够同相叠加;而多途干扰信号无法实现同相叠加，对于宽带码元信号来说有白化的趋势，因而增加了接收信号的信干比(SIR)，突出了主要路径的信号功率，从而达到抑制多径干扰的效果，使得信道冲击响应函数逼近于δ 函数。

4 仿真研究

为验证方法的有效性，对其进行了仿真实验。通信数据帧如图3所示，由同步码、间隔码和信息码构成。同步码采用脉宽50 ms，带宽为3～8 kHz 的LFM 信号，其频带覆盖发射换能器的工作频带。间隔码的作用使同步码与信息码之间留有一定的时隙间隔，一般应大于信道的最大多途时延扩展。整个系统工作频带选择5～8 kHz，采样率60 kHz;系统分为2 个通信子频带，每个子频带产生一个码元集合，分割为脉宽10 ms，带宽1 kHz，中心频率间隔100 Hz的16 个LFM 码元信号。每个码元可以携带4 bit 信息，而一个码元符号由2 个LFM 码元构成，这样通信速率最高可达800 bit/s.

图3 数据帧结构Fig.3 Structure of data frame

声波是水声通信中传递信息的载体，而水体是声波传输的介质，因而通信地区水体环境就可以被认为是水声通信信道。由于声波在水中的传播速度(1 500 m/s)远小于无线电波在空气中的传播速度，因而水声信道的一个突出特点就是信号的多途扩展时延非常严重(在某些深海水域多途时延甚至能达到秒的量级)，这对于水声通信来说是一个难点。另外，由于通信水域水文条件的变化和水底地形地貌的不同使得多途信号所受的畸变严重，在接收端呈现复杂的干涉叠加现象，因此想要精确的仿真出水声通信信道是比较困难的事情。然而，利用射线声学可以大致描述水声信道的一些特点，根据当地的水文环境参数可以计算出信道的冲击响应函数［1］，这已被实验所证实。因此，在本文中，利用某声纳预报软件，根据实测声速分布、水文数据和实验装置的布放(发射换能器布放深度20 m，接收换能器布放深度30 m，距离5 000 m)，计算出某海域的信道冲击响应函数，图4(a)中显示的是利用发射信号中同步信号的拷贝相关估计出的信道冲击响应函数。从图中可以看出信道多图扩展比较严重，发射信号经过多次海底海面反射在接收端叠加;接收信号幅度呈指数衰减，说明具有大时延量的路径传播距离长，传播损失造成的信号幅度衰减也大。图4(b)显示的是接收信号经过Rake 接收机处理之后估计出的信道冲击响应函数，可见Rake 接收机对信道多途效应进行补偿后突出信号中主要路径成分，提高直达声的信噪比，使得信道的冲击响应函数逼近δ 函数的形式，实现了抑制接收信号中多途效应的干扰。

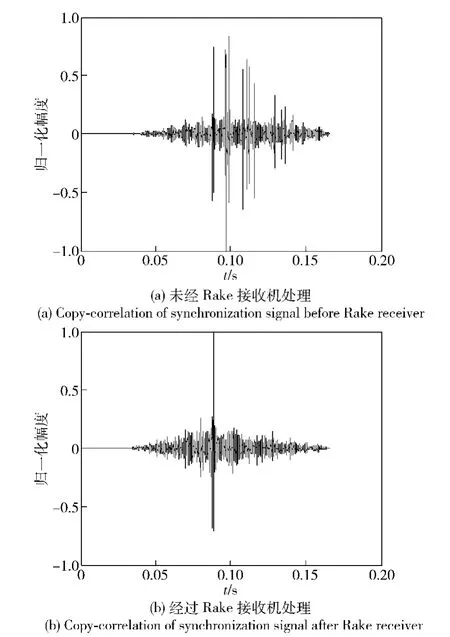
图4 同步信号拷贝相关估计的信道冲击响应Fig.4 CIR estimation with copy-correlation of synchronous signal before and after Rake receiver

图5显示的是相同条件下文中所提FRFT-PPM调制方法与MFSK 调制方式的误码率性能比较。在不加信道编码、误码率为10-3时，FRFT-PPM 较MFSK 有9 dB 信噪比的增益，这意味着FRFT-PPM 可以在较远的通信距离上取得良好的通信效果，究其原因是因为以宽带信号为载波的信号处理增益要远大于窄带信号，这就使得FRFT-PPM 具有良好的稳健性。

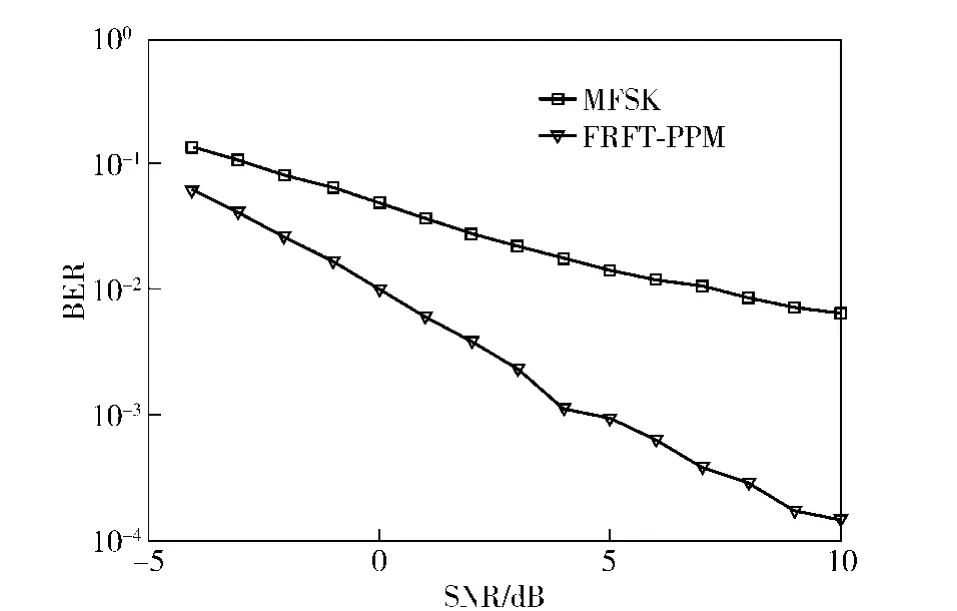
图5 两种调制方法的误码性能对比Fig.5 BER comparison between FRFT-PPM and MFSK

本文针对不同的海洋信道做了大量的仿真研究，验证该通信体制的鲁棒性。表1简单例举了3～10 km 几种典型海洋信道，针对每种信道采用100次蒙特卡洛仿真，每次传输3 200 bit 信息，统计相应各信道误码率如表1所示。

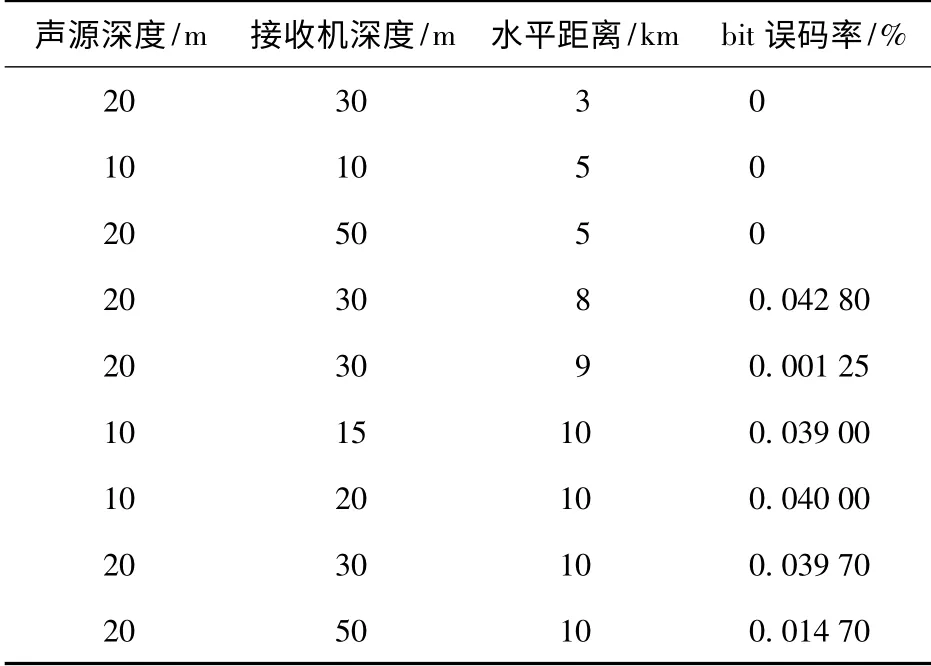
表1 不同海洋信道的仿真结果Tab.1 Simulation results for different ocean channels

5 结论

文中给出了一种基于分数阶Fourier 变换的水声通信方案，并对其进行详细的理论公式推导和仿真验证，在保证通信的有效性和稳健性的前提下较好的提高了远程水声通信的通信速率。由于采用LFM 信号作为信息调制的载波信号，采用分数阶Fourier 变换作为信息解调手段，因而有着很强的抗干扰能力和很好的鲁棒性，非常适合于低信噪比的工作环境和远程水声通信。另一方面，基于Rake 接收机的多径分集接收技术能够有效的抑制水声信道的多途干扰，这对于信道条件复杂的水声通信环境来说具有极大的优势，因此本方案可应用于复杂的水下工作环境，拥有非常广阔的应用前景。

References)

［1］ 惠俊英.水下声信道［M］.北京:国防工业出版社，1992.HUI Jun-ying.Underwater acoustic channel［M］.Beijing:National Defense Industry Press，1992.(in Chinese)

［2］ 田坦，刘国枝，孙大军.声呐技术［M］.哈尔滨:哈尔滨工程大学出版社，2000.TIAN Tan，LIU Guo-zhi，SUN Da-jun.Techniques of sonar［M］.Harbin:Harbin Engineering University Press，2000.(in Chinese)

［3］ 陶然，邓兵，王越.分数阶Fourier 变换在信号处理领域的研究进展［J］.中国科学(E 辑)，2006，36(2):113-136.TAO Ran，DENG Bing，WANG Yue.Research advance in fractional Fourier transforms in the signal processing region［J］.Science in China Ser E Information Science，2006，36(2):113-136.(in Chinese)

［4］ 殷敬伟，惠俊英，蔡平，等.分数阶Fourier 变换在深海远程水声通信中的应用［J］.电子学报，2007，35(8):1499-1504.YIN Jing-wei，HUI Jun-ying，CAI Ping，et al.Application of fractional Fourier transform in long range deep-water acoustic communication［J］.Acta Eletronica Sinica，2007，35(8):1499-1504.(in Chinese)

［5］ Almeida L B.The fractional Fourier transform and time-frequency representation［J］.IEEE Transaction Signal Processing，1994，42(11):3084-3091.

［6］ Pei S C，Yeh M H，Tseng C C.Discrete fractional Fourier transform based on orthogonal projections［J］.IEEE Transaction Signal Processing，1999，47(5):1335-1348.

［7］ Candan C，Kutay M A，Ozaktas H M.The discrete fractional Fourier transform［J］.IEEE Transaction Signal Processing，2000，48(5):1335-1348.

［8］ Ozaktas H M，Arikan O，Kutay A A，et al.Digital computation of the Fourier transform［J］.IEEE Transaction Signal Processing，1996，44(9):2141-2150.

［9］ Pei S C，Ding J J.Closed-form discrete fractional and affine Fourier transform［J］.IEEE Transaction Signal Processing，2000，48(5):1338-1353.

［10］ Santhanam B，McClellan J H.The discreet rotational Fourier transform［J］.IEEE Transaction Signal Processing，1996，44(4):994-998.

［11］ Massimiliano M M.A multicarrier system based on the fractional fourier transform for time-frequency-selective channels ［J］.IEEE Transaction on Communications，2001，49(6):994-998.

［12］ Tang Q L，Yang L Q，Qin T F，et al.Energy-saving PPM schemes for WSNs［J］.Science in China Series F:Information Science，2008，51(5):571-585.

［13］ Zayed A I.A convolution and product theorem for he fractional Fourier transform［J］.IEEE Signal Processing Letters，1998，5(4):101-103.

［14］ 仇佩亮，陈恵芳，谢磊.数字通信基础［M］.北京:电子工业出版社，2007.QIU Pei-liang，CHEN Hui-fang，XIE Lei.Foundational digital communication［M］.Beijing:Publishing House of Electronics Industry，2007.(in Chinese)