Hilbert空间Cd中框架的若干性质

杨 莹, 曹怀信*, 李 静， 雷娟霞

(1.陕西师范大学数学与信息科学学院, 陕西 西安 710062; 2.陕西铁路工程职业技术学院, 陕西 渭南 714000)

0 引 言

框架的概念最早由Duffen和Schaeffer在1952年研究非调和Fourier时提出[1]. 1989年, Heil和Walunt将框架理论与Gabor变换相结合[2], 使得框架理论有了初步的发展. 此后, 大批学者对此进行了深入的研究. 20世纪90年代, Grochenig、Aldroubi[4]、 Sun和Tang[4]开始研究Banach空间中的框架理论. 孙文昌[5,6]教授引入Hilbert空间中g-框架的概念, 这一定义包含了以往研究过的所有框架, 例如：伪框架、外框架、斜框架、有界伪框架以及子空间框架等. 曹怀信教授[7]提出并研究了Banach空间的(p,Y)-算子框架与p阶框架. 近年来, 框架理论已经成为一个应用广泛、生机勃勃的热点研究领域, 同时也成为信号处理、图像处理及数据压缩等各种技术的重要工具之一. 框架的快速发展广泛汲取了各个领域的知识, 而将框架与物理概念特别是量子力学相结合也为框架的发展提供新的契机. 本文将讨论d维Hilbert空间Cd中框架的一系列重要性质，用Fd(A,B)表示Cd中所有以A,B为框架下、上界的框架之集，用Md(A,B)表示期望下界为A, 上界为B的d阶正定矩阵之集，研究框架集Fd(A,B)与矩阵集Md(A,B)的一系列重要性质，并揭示它们之间的关系.

1 预备知识

为了证明本文的主要结果, 先给出以下定义和相关结论.

定义2.1∀C∈Md,∀φ∈S(Cd), 定义矩阵C关于φ的期望为Eφ(C)=〈φ|C|φ〉.显然有如下性质：(1)Eφ(·)是线性的；(2)Eφ(·)是连续的.

定义2.2用Md(A，B)表示期望下界为A, 上界为B的d阶正定矩阵之集, 即

用Fd(A,B)表示Hilbert空间Cd的以A为框架下界、B为框架上界的全体框架之集.

2 主要结果

证明(1)因为∀φ∈S(Cd), 有

任取单位向量e∈Cd, 令

所以,A≤Eφ(C)≤B,∀φ∈S(Cd)， 因此,C∈Md(A,B)， 显然π(C)=f. 证毕.

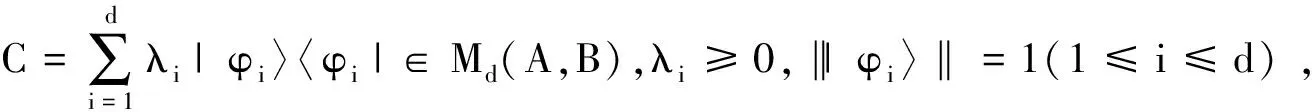
其中λmax=max{λ1,…,λd},λmin=min{λ1,…,λd}.

证明∀φ∈S(Cd) , 有

故TCT+∈Md(λminA,λmaxB). 证毕.

定理2.5若C∈Md(A,B),T为下有界的压缩算子, 则T+CT∈Md(AM2,B).

证明因为T为下有界的压缩算子, 所以存在常数M>0,使得

因为C∈Md(A,B), 所以A≤‖C‖≤B,B-1≤‖C-1‖≤A-1. 一方面有

另一方面,

于是,T+CT∈Md(AM2,B) . 证毕.

定理2.6若C∈Md(A,B),T为有界可逆算子, 则T+CT∈Md(‖T-1‖-2A,‖T‖2B).

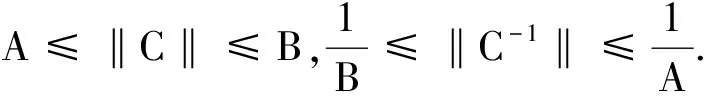
另一方面,Eφ(T+CT)=‖C1/2T|φ〉‖2≥‖C-1/2‖-2‖T|φ〉‖2≥‖C-1‖-1‖T-1‖-2≥‖T-1‖-2A. 于是T+CT∈Md(‖T-1‖-2A,‖T‖2B). 证毕.

定理3.7(1)Md(A,B)是Md中的闭凸集, 且AId与BId是Md(A,B)的端点；

(2)Id∈Md(A,B)⟺A≤1≤B；

(3)Dd⊂Md(d-1,1).

证明(1)设C1,C2∈Md(A,B) ,且λ1,λ2≥0,λ1+λ2=1, 则

A≤Eφ(λ1C1+λ2C2)=λ1Eφ(C1)+λ2Eφ(C2) ≤B,∀φ∈S(Cd)

可见λ1C1+λ2C2∈Md(A,B). 故Md(A,B)是凸集.

设Cn∈Md(A,B)(n=1,2,…),Cn→C(n→∞), 则

A≤Eφ(Cn) ≤B,∀n≥1,∀φ∈S(Cd)

因而A≤Eφ(C)≤B,∀φ∈S(Cd),故Md(A,B)是闭的.

设C,D∈Md(A,B),AI=tC+(1-t)D,0

A=Eφ0(AI)=tEφ0(C)+(1-t)Eφ0(D)>tEφ0(C)+(1-t)Eφ0(C)=Eφ0(C)

这与A≤Eφ0(C)矛盾, 所以∀φ∈S(Cd), 有Eφ(C)=Eφ(D)=A, 因此C=AI,D=AI. 于是AI∈Ext(Md(A,B)). 同理BI∈Ext(Md(A,B)).

(2)(⟹)：Id∈Md(A,B), 则有A≤Eφ(Id)≤B,∀φ∈S(Cd), 即A≤1≤B.(⟸)：设A≤1≤B. 因为

Eφ(Id)=〈φ|Id|φ〉=〈φ|φ〉=1,∀φ∈S(Cd)

于是A≤Eφ(Id)≤B,∀φ∈S(Cd), 从而Id∈Md(A,B).

(1)若C∈Md(A1,B1),D∈Md(A2,B2), 则C+D∈Md(A1+A2,B1+B2)；

(2)若C∈Md(A,B), 则λC∈Md(λA,λB)；

(3)若C∈Md1(A1,B1),D∈Md2(A2,B2), 则

A1+A2≤Eφ1⊕φ2(C⊕D)≤B1+B2,∀φ1∈S(Cd1),φ2∈S(Cd2)

(4)若C∈Md1(A1,B1),D∈Md2(A2,B2), 则

A1A2≤Eφ1⊗φ2(C⊗D)≤B1B2,∀φ1∈S(Cd1),φ2∈S(Cd2)

(5)若C∈Md(A1,B1),D∈Md(A2,B2),且B2

C-D∈Md(A1-B2,B1-A2)

证明(1)若C∈Md(A1,B1),D∈Md(A2,B2) 由定义知

A1≤Eφ(C)≤B1,A2≤Eφ(D)≤B2,∀φ∈S(Cd)

于是A1+A2≤Eφ(C+D)≤B1+B2,∀φ∈S(Cd), 故C+D∈Md(A1+A2,B1+B2).

(2)若C∈Md(A,B), 由定义知A≤Eφ(C)≤B,∀φ∈S(Cd), 于是

λA≤Eφ(λC)≤λB,∀λ∈R+,∀φ∈S(Cd)

故λC∈Md(λA,λB).

(3)因为C∈Md1(A1,B1),D∈Md2(A2,B2), 所以由定义知

A1≤Eφ(C)≤B1,∀φ∈S(Cd1),A2≤Eφ(D)≤B2,∀φ∈S(Cd2)

于是∀φ1∈S(Cd1),φ2∈S(Cd2) , 有

A1+A2≤Eφ1⊕φ2(C⊕D)=Eφ1(C)+Eφ2(D)≤B1+B2

(4)因为C∈Md1(A1,B1),D∈Md2(A2,B2), 所以由定义知

A1≤Eφ(C)≤B1,∀φ∈S(Cd1),A2≤Eφ(D)≤B2,∀φ∈S(Cd2)

于是,∀φ1∈S(Cd1),φ2∈S(Cd2), 有

A1A2≤Eφ1⊗φ2(C⊗D)=Eφ1(C)·Eφ2(D)≤B1B2

(5)因为C∈Md(A1,B1),D∈Md(A2,B2), 所以由定义知

A1≤Eφ(C)≤B1,A2≤Eφ(D)≤B2,∀φ∈S(Cd)

于是, -B2≤-Eφ(D)≤-A2,∀φ∈S(Cd), 从而

0

因此C-D∈Md(A1-B2,B1-A2). 证毕.

参考文献

[1] Duffin R J, Schaeffer A C. A class of non harmonic Fourier series[J].Transactions of the American Mathematical Society, 1952, 72(2): 341-366.

[2] Heil C, Walnutw D. Continuous and discrete wavelet transforms[J]. SIAM Review, 1989, 31(4): 628-666.

[3] Grochenig K. Describing functions:atomic decompositions versus frames[J]. Monatshefte für Mathematik, 1991, 112(1): 1-41.

[4] Aldroubl A, SUN Q Y, TANG W S. P-frames and shift invariant subspaces ofLp[J]. The Journal of Fourier Analysis and Applications, 2001, 7(1): 1-22.

[5] SUN W C. G-frames and g-Riesz bases[J]. Journal of Mathematical Analysis and Applications, 2006, 322(1): 437-452.

[6] SUN W C. Stability of g-frames[J]. Journal of Mathematical Analysis and Applications, 2007, 326(2): 858-868.

[7] CAO H X, LI L, CHEN Q J,etal. (p,Y)-Operator frames for a Banach space[J]. Journal of Mathematical Analysis and Applications, 2008, 347(2): 583-591.

[8] Christensen O. An Introduction to Frames and Riesz Bases[M], 2002: 344-355.

[9] 朱红鲜. Hilbert空间中框架与Riesz基的扰动及其正交分解[D]. 西安:陕西师范大学硕士学位论文, 2003: 1-39.

[10] 邹玉梅. Hilbert空间中的框架及广义框架的相关性质[D].西安:陕西师范大学硕士学位论文, 2002: 1-34.

[11] LI S, OGAWA H. Pseudo frames for subspaces with applications[J]. The Journal of Fourier Analysis and Applications, 2004, 10(1): 409-431.

[12] Christensen O, Eldar Y. Dual frames and shift-invariant spaces[J]. Applied and Computational Harmonic Analysis, 2004, 17(4): 48-68.

[13] Fornasier M. Quasi-orthogonal decompositions of structured frames[J]. Journal of Mathematical Analysis and Applications, 2004, 289(1): 180-199.

[14] Khosravi A, Kamran M. Fusion frames and g-frames[J]. Journal of Mathematical Analysis and Applications, 2008, 342(1): 1 068-1 083.

[15] Cao H X. Bessel sequences in a Hilbert space[J]. J. Eng. Math., 2000, 17(2): 92-98.

[16] 李春艳, 曹怀信. Banach空间中的框架与Riesz基[J]. 数学学报, 2006, 49(6): 1 361-1 366.

[17] 李春艳, 曹怀信. Banach空间中框架的独立性[J]. 河北师范大学学报, 2007, 31(2): 159-162.

[18] 陈峥立,曹怀信,陆 玲. Hilbert空间中几种基的关系[J]. 西北大学学报, 2008, 30(3): 345-353.

[19] 郅伟萍, 曹怀信. 框架的冗余性及其对小波重构的影响[J]. 宝鸡文理学院学报, 2007, 27(1): 1-4.