多电平变换器拓扑关系及新型拓扑
王琛琛 李永东
(1.北京交通大学电气工程学院 北京 100044 2.清华大学电力系统国家重点实验室 北京 100084)
1 引言
多电平变换器从产生至今已经有近三十年的发展历史,其间产生了大量的拓扑结构。研究多电平拓扑的目的是为了实现多电平输出,使变换器能够应用于更高电压等级的场合,提高输出电压的谐波性能。研究各种拓扑的特点,分析并明晰各种拓扑之间的联系和区别,对于进一步研究拓扑具有重要意义。本文首先对多电平变换器拓扑的发展做了一个回顾和讨论,整理了多电平变换器发展演变的思路,分析了多电平拓扑之间的联系,提出了通用多电平拓扑简化为其他拓扑的规律,在此基础上提出两种新的多电平拓扑结构,并对其工作原理和控制策略进行了仿真研究。
2 基本拓扑
2.1 三极单元变换器
实现多电平的最简单直接的方法就是构造一个多级直流电压源串联,且每级都有可控的独立输出通路,如图1a 所示。这样的思想早在文献[1]中就已经被提出来。但是受当时开关器件发展水平的限制,文章中采用反并联的晶闸管来实现这个开关的功能,晶闸管不能关断的缺点造成了不同等级电压通路之间的换流过程极其复杂,大大增加了控制的难度。
类似这种思想,文献[2]给出了一个最初的三电平结构,如图1b 所示,由二极管和三极管组成的两

图1 多级电压源串联思想构成多电平变换器结构 Fig.1 Schematic of multilevel converter structure
个单向回路构成了0 电平的输出通路,实现了三电平的电压输出。随着电力电子器件的发展,考虑到各开关管承受压降的统一性,最终得到比较实用的拓扑如图2a 所示,被称为层叠换流单元(stacked commutation cells)或者三极单元(three-pole cells)。其可以采用如图2b 所示的导通策略,使得最外侧支路的两个管子中一个管子在半个周期中处于频繁开关状态,另一个管子每个基波周期只开关一次,可以大大减小损耗,同时也可以避免串联器件同时开通和关断带来的均压问题。
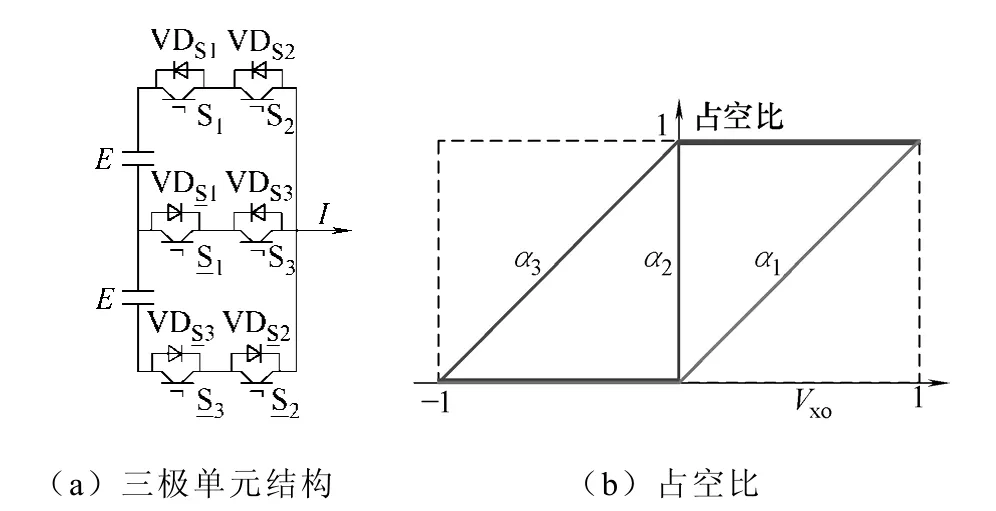
图2 三极单元变换器结构及导通规律 Fig.2 Schematic of three-pole cell structure
2.2 二极管钳位型多电平变换器
与此同时,另外一种结构中点钳位型(Neutral- Point-Clamped,NPC)也被提出来[2-3],这也是现在使用最为广泛的一种三电平结构。NPC 可以看成是三极单元的一种特殊的实现方式[4],三极单元中实现双向电流通路功能的支路被如图3a 所示的两个内部开关管和两个钳位二极管(VDN1,VDN2)构成的两个电流单向支路所代替,节省了开关器件,简化了结构。
NPC 的多电平形式就是二极管钳位型多电平变换器(diode clamped multilevel converter)。图3b、图3c 给出了五电平情况下的两种拓扑形式。
二极管钳位型多电平结构有固有的缺点[5-6]:
(1)为了保证钳位二极管承受相同的反向电压E,钳位二极管的数目将按照电平数的二次方快速增加。
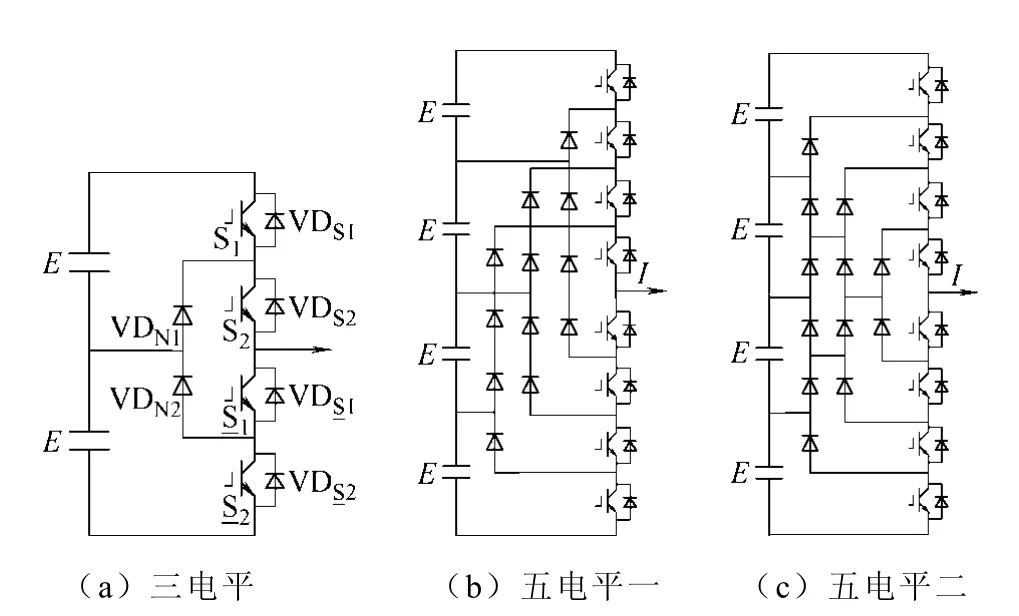
图3 二极管钳位型多电平变换器结构 Fig.3 Diode-clamped multilevel converter structure
(2)如果采用单一直流电源供电,母线上各个电容的电压很难控制平衡。
(3)内外管的开关应力(switching stress)或者说损耗存在不平衡。
(4)钳位二极管只能保证最外面的开关管被 可靠钳位,而内部的开关管并没有被直接钳位[5]。
2.3 电容钳位型多电平变换器
文献[7]利用增加的钳位电容构成了混合钳位拓扑(见图4a),有利于解决NPC 拓扑中内管不能可靠钳位以及直流母线电容平衡的问题。利用电容作为钳位器件给多电平拓扑提供了一个新的思路。单纯采用电容钳位的思想最早出现在文献[8]中(见图 4b)。在此基础上,Meynard[4,9-10]将其拓展到多电平领域,称为电容钳位型多电平变换器(flying capacitor multilevel converter),也称为Multicell 或者Imbricated cells。
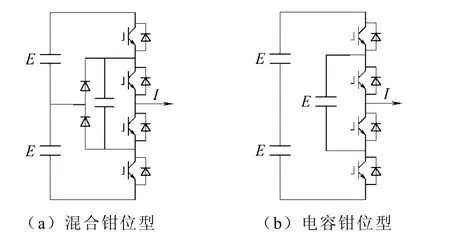
图4 混合钳位型和电容钳位型变换器 Fig.4 Diode-capacitor and capacitor clamped structure
电容钳位型多电平的钳位电容除了具有钳位作用以外,其本身所具有的电压输出能力也增加了变换器输出某一电平的开关状态。电容钳位型变换器不存在母线电容电压不平衡、开关管之间开关应力不同以及耐压不平衡的问题。但是随着电平数增加,钳位电容的数量大大增加,增加了系统的成本和体积。另外在应用中,电容的故障率要远远高于半导体器件的故障率,钳位电容的引入影响了整个系统的寿命和可靠性。
2.4 有源中点钳位型变换器
为了进一步解决NPC 中非直接钳位和开关应力不同的问题,文献[11-12]提出了有源中点钳位型变换器(Active NPC,ANPC),如图5a 所示。ANPC结构采用带反并联二极管的开关管来代替钳位二极管,多用了两个开关管。而在实际采用IGBT 的NPC系统中,出于器件特性一致的考虑,一般用IGBT中寄生的反并联二极管来做钳位二极管。ANPC 结构利用了原先闲置的IGBT 开关管和反并联二极管一起保证可靠的钳位。另外,ANPC 增加的两个开关管可以增加零电平时刻的电流通路,选择合适的电流通路可以把原来内管上的损耗一定程度分散到钳位开关管上。文献[11-12]经过分析得到,采用ANPC 的结构可以比传统的NPC 提高20%的系统容量或者85%的开关频率,这对于实际应用很有价值。文献[13]结合了NPC 和三极单元,也给出了一种新的三电平结构,称为Stacked NPC,如图5b 所示。它通过增加电流通路,也能够有效地平衡各管之间的损耗。
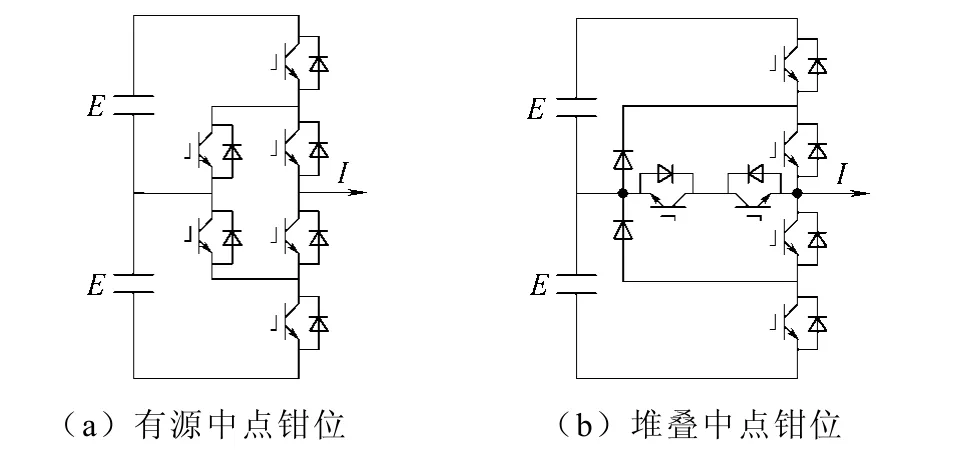
图5 有源中点钳位和堆叠中点钳位三电平变换器 Fig.5 Active NPC and stacked NPC converter
3 衍生拓扑
上面给出的四种基本拓扑,除了根据自身的特点往更高电平拓展之外,还可以通过适当的组合和变形,构成新的拓扑。
3.1 层叠式多单元变换器
层叠式多单元变换器( Stacked Multicell Converter,SMC)可以认为是Multicell 和P-pole cell两种多电平拓扑思想结合的产物[4]。图 6 是一个SMC 的结构图[14]。在输出相同电平数的情况下,SMC 能在不损失Multicell 动静态性能的同时大大减少钳位电容的数量。
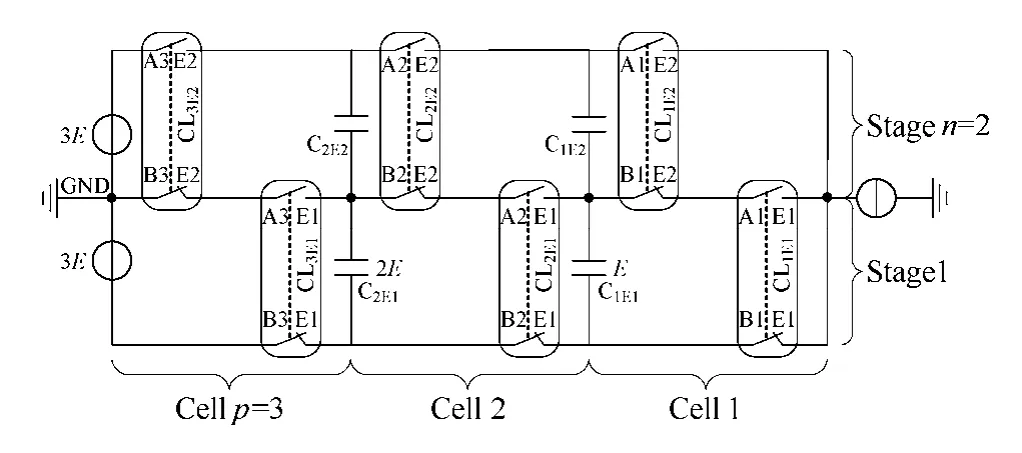
图6 3×2 层叠式变换器拓扑 Fig.6 3×2 stacked multicell converter
对于这样一个n×p 的层叠式多单元变换器(n代表单元数,p 代表堆叠数),可以看成是p 个n 单元的Multicell 层叠而成,也可以看成n 个p-pole cell 连接得到。图7a 所示是一个SMC 结构的扩展,可以看成是多个三极单元通过电容串联而成。另外NPC 作为三极单元的一种特殊方式,也可以作为最后一级接到SMC 拓扑当中,如图7b 所示。
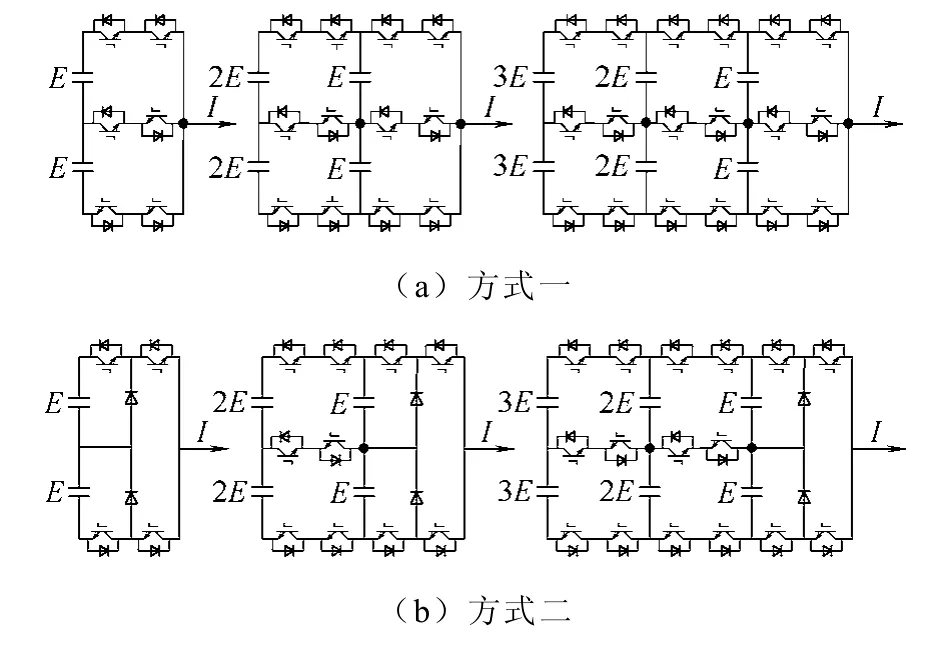
图7 层叠式变换器拓扑的扩展 Fig.7 Extension of the SMC
3.2 有源中点钳位型多电平变换器
和NPC 类似,ANPC 结构也很容易直接推广到多电平。不过如果把ANPC 和Multicell 结合就可以得到新的拓扑结构—有源中点钳位型多电平变换器(ANPC multilevel converter)[15]。图8a 所示就是这样一个 ANPC 的五电平结构,其中三个单元(图中点划线框所示)都可以看成是电容钳位的三电平结构,然后按照ANPC 的结构组合起来构成一个五电平的新拓扑。进一步省去电容还可以得到如图8b 和图8c 的两种结构[15-16]。图8a 中断开处可以按照电容钳位型的方式继续扩展到更高电平。需要注意的是,ANPC 和SMC 都只能实现奇数电平的输出。

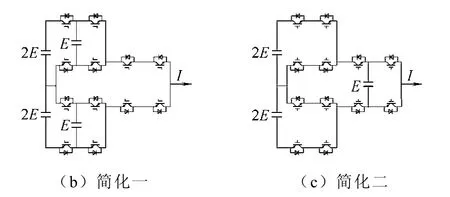
图8 有源中点钳位型多电平变换器 Fig.8 ANPC multilevel converter
3.3 通用多电平拓扑结构
从之前给出的拓扑图注意到,不同的拓扑结构为了实现一定数目的电平输出,其在外侧的主开关管的分布是一致的,主要的区别在于钳位器件的不同。二极管、可控开关管以及电容都可以单独或者组合之后被选择作为辅助器件。
文献[17]提出了一种通用多电平拓扑结构。在这个拓扑中,二极管、可控开关管和电容这三种钳位器件同时被使用,可以认为是最复杂同时也是最全面的一种结构。如图9 是一个五电平的通用拓扑结构。通用多电平拓扑采用了大量的钳位开关管、二极管和电容,通过特定开关模式可以实现电容电压的自平衡。
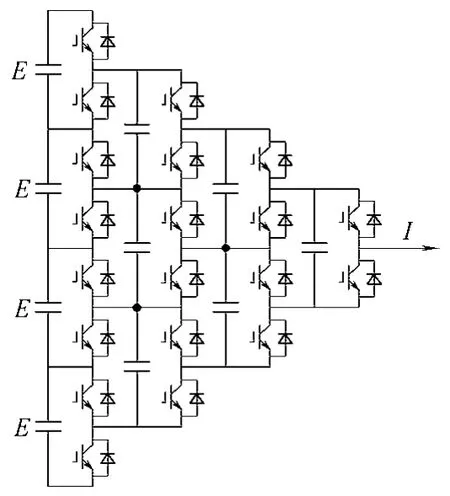
图9 五电平通用多电平拓扑 Fig.9 5-level generalized multilevel converter
4 通用拓扑和其他拓扑之间的关系
通用拓扑同时使用了三种钳位器件,可以认为是其他拓扑的一种高度概括。前面所述的基本拓扑及衍生拓扑都可以通过一定的简化从通用拓扑中得到。以图9 所示的五电平通用拓扑为例,如果保留钳位二极管和电容,省去所有的钳位开关管,通用拓扑就简化成混合钳位型拓扑;在此基础上如果省掉所有的钳位电容或者二极管,则退化成二极管钳位型或者电容钳位型拓扑,如图10 所示。

图10 通用拓扑简化为混合、二极管和 电容钳位型拓扑 Fig.10 Diode-clamped and flying capacitor-clamped topologies deduced from the generalized topology
除此之外还发现,通过适当的简化,通用拓扑还可以退化为SMC 和ANPC 等结构。如图11a 所示,五电平的通用拓扑经过简化可以退化为一个2×2 的SMC 结构,只是在最后一级采用的是NPC结构。考虑到NPC 是三极单元的一种变形,因此并不影响理解通用拓扑和SMC 之间的联系。同样的,如图 11b 所示,通用拓扑经过简化也可以退化成ANPC 的结构。
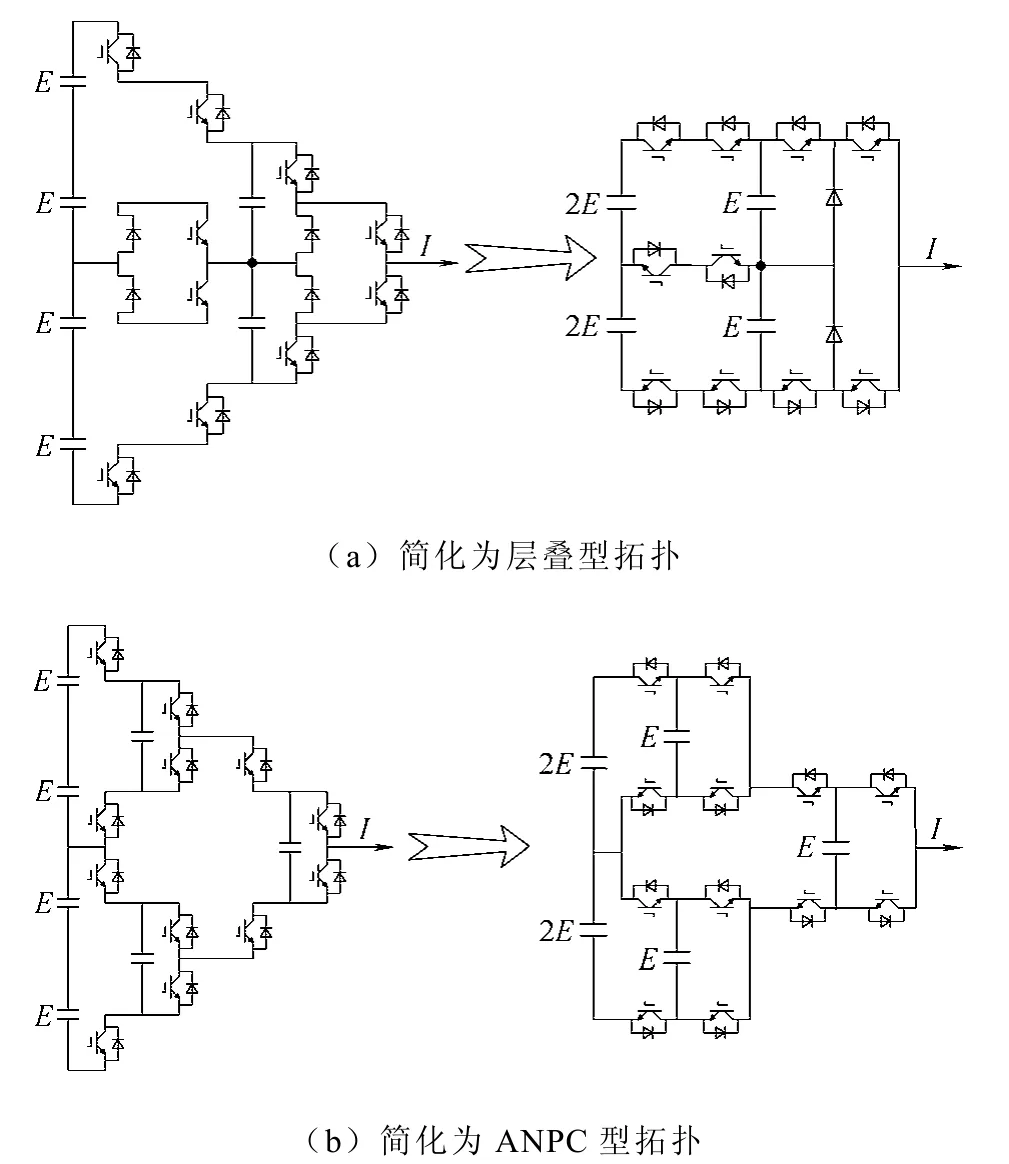
图11 通用拓扑简化为层叠型和ANPC 型拓扑 Fig.11 SMC and ANPC topologies deduced from the generalized topology
现只给出了五电平的例子,其他电平的情况可以类似得到。可以看出,现有的多电平拓扑和通用拓扑之间存在着紧密的联系,通用拓扑通过适当的简化可以退化成这些常用的拓扑结构。图12 以图表的形式对这些关系做了一个总结。
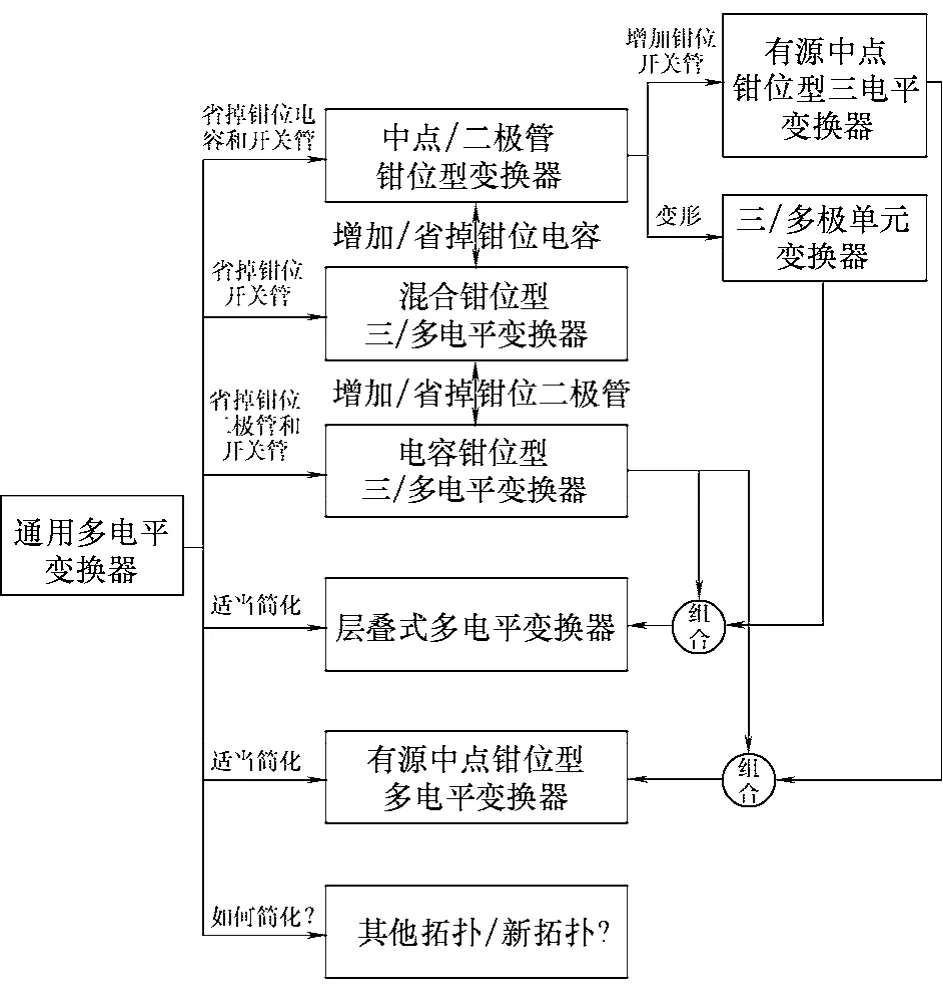
图12 通用拓扑和已有拓扑之间的关系 Fig.12 Relationship between the existing topologies
那么在通用拓扑的简化过程中,有哪些需要遵守的规律呢?总结出以下几点:
(1)两侧主开关管必须全部保留。
(2)钳位开关管、二极管和电容要对称地从两侧成对省略。简化后拓扑具有很好的对称性,且可扩展。
(3)如果要使简化后拓扑具有完整输出所有 电平的能力,通用拓扑中对应每个电平的多个电流双向通路至少有一个被保留。
(4)出于实际应用的考虑,钳位电容要越少越好,尤其是尽可能地去掉靠近直流母线侧的钳位电容。
(5)为了保证能够有效地控制每个钳位电容 电压稳定,在输出特定电平、特定电流情况下,存在对钳位电容电压没有影响或者影响相反的开关状态。
不难得到,前文所述的从通用拓扑退化到各种已有拓扑的过程都遵循了这些规律。这不但对理解拓扑之间的关系有重要作用,对于通过简化通用拓扑、提出新的拓扑结构也有很重要的指导意义。
进一步的,通用多电平拓扑结构经过简化可以得到如图13 的结构,这就是所熟知的H 桥级联型拓扑。这个结构早在20 世纪70 年代中就已经被提出[18],后来结合了PWM 的控制策略得到了广泛使用。可以看到,图13 右边所示的两个H 桥级联一样能够输出五电平。不同的是,级联结构是每级独立供电,而不像前面所叙述的众多拓扑结构是通过母线统一供电的。虽然级联型拓扑和前面所述的众多拓扑的构造思想有很大差别,但是对于H 桥级联型拓扑以及其他的级联型拓扑,例如三电平级联,或者是混合级联结构都可以从通用拓扑中找到其痕迹。

图13 通用拓扑和H 桥拓扑之间的关系 Fig.13 Relationship between H-bridge and generalized topology
5 新型多电平变换器拓扑
本文遵循前面归纳出来的通用拓扑简化过程中的规律,提出了如图14 所示的两种新的多电平拓扑结构。可以看到这两种新拓扑都能够实现五电平的输出,而且结构相似,运行原理也基本相同。相比较而言,图14b 所示的拓扑结构更加清晰简单,因此后续具体的分析和讨论将会围绕该拓扑展开,图14a 所示拓扑的相关分析可以类比得到。另外,图14b 所示拓扑在图15a 所示的断点处继续扩展可以得到更高电平,例如图15b 就给出了一个七电平的例子。
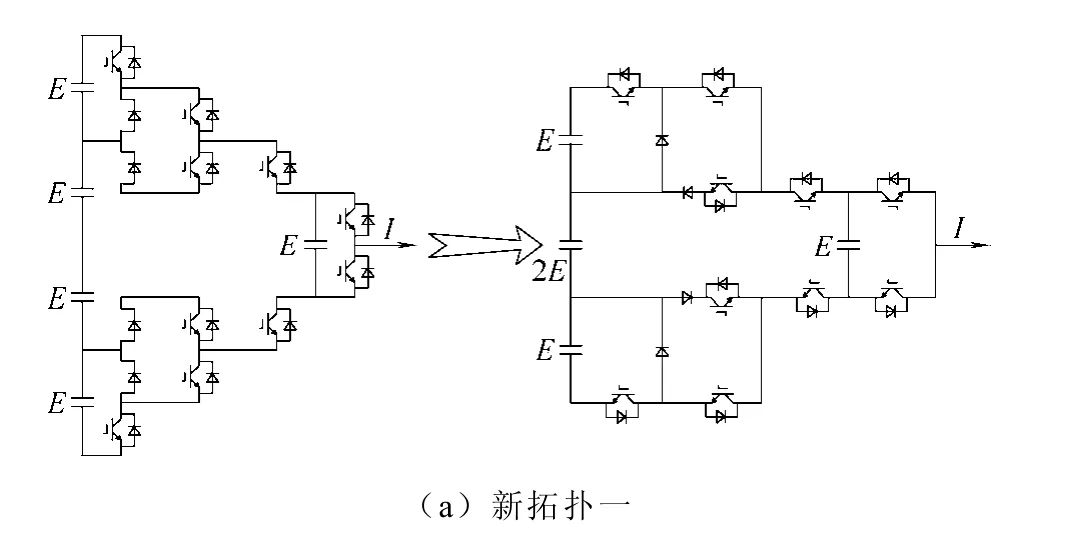
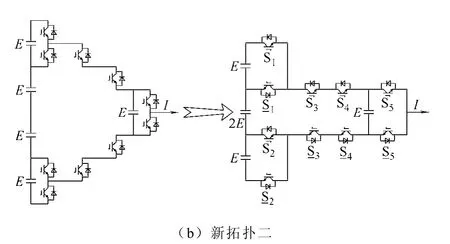
图14 两种新拓扑结构 Fig.14 Two novel multilevel topologies
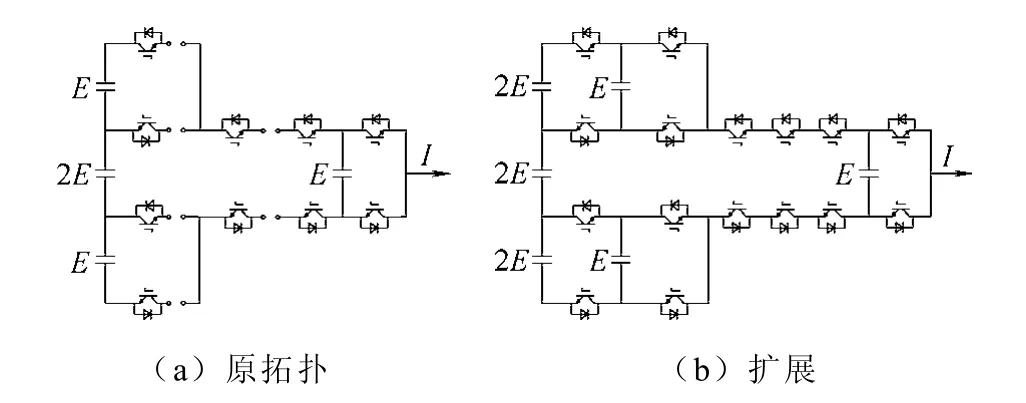
图15 新拓扑结构的扩展 Fig.15 Extension of the novel topology
为了和现有的拓扑结构比较,表1 以五电平为例,对各种拓扑结构所用的器件数目进行了统计。从这个表中可以比较各种拓扑所需的开关管、二极管以及钳位电容的数目。可以看到,本文所提出的新拓扑和简化后的ANPC 从使用器件数目上来看具有很大的优势,其中图14b 拓扑的所需器件最少。以图14b 所示的新拓扑结构为例,对新拓扑的工作原理进行分析。所有可能的开关状态见表2,对应了0~4E 共五个输出电平。
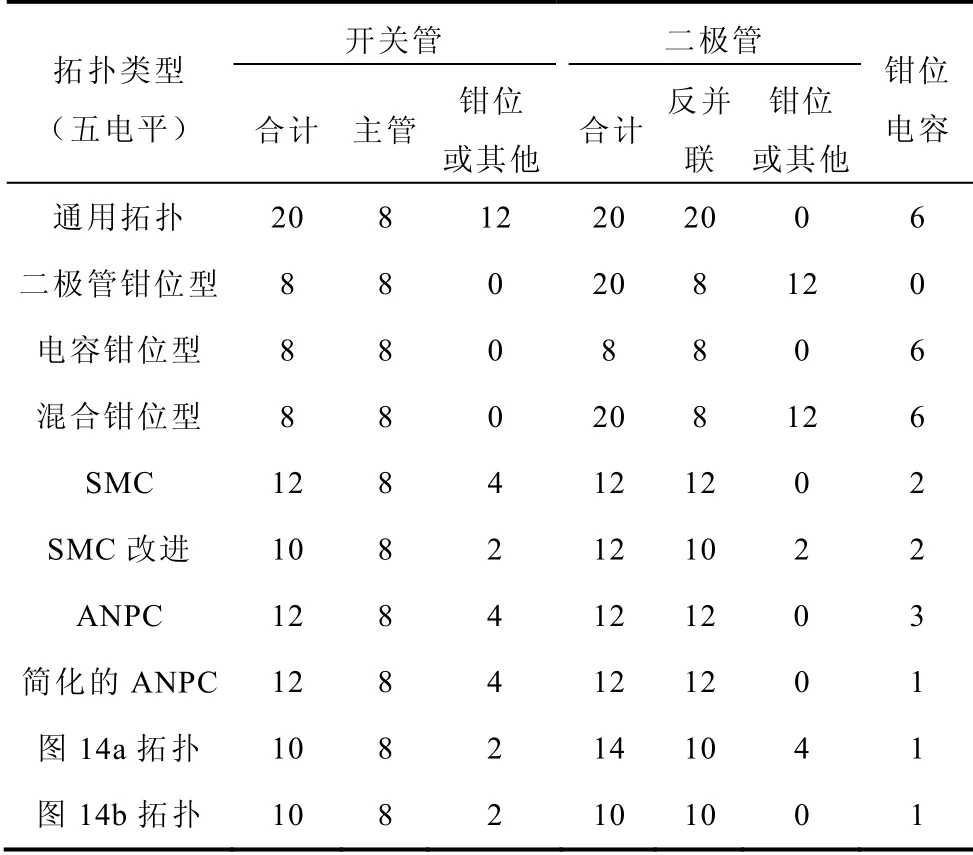
表1 多电平拓扑所用器件数目比较 Tab.1 Devices required in different topologies
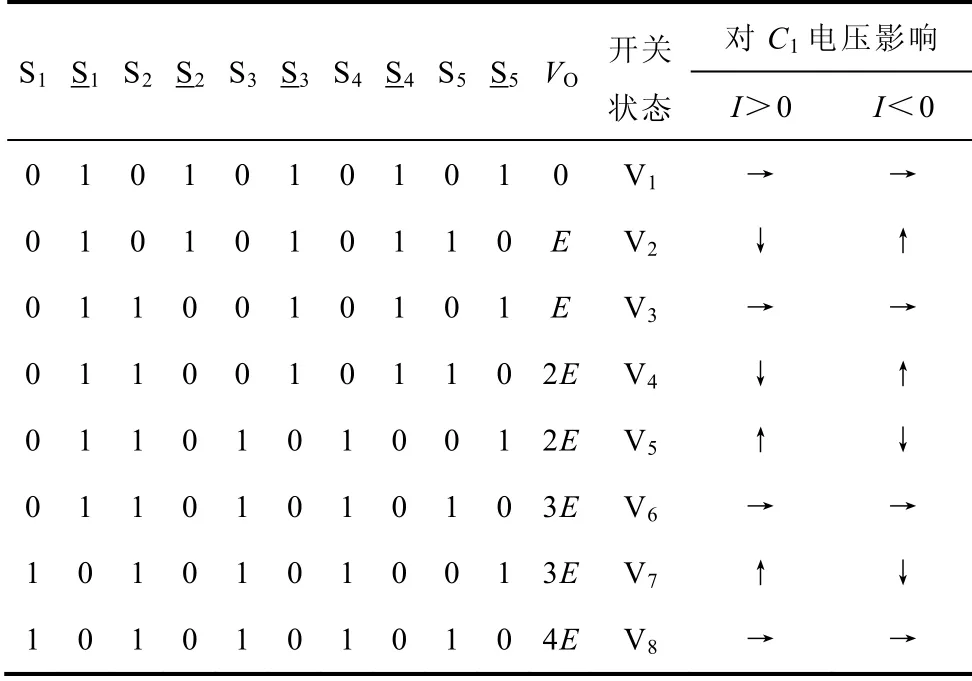
表2 新拓扑结构的开关状态 Tab.2 Switching states of the novel topology
该拓扑能够正常工作的一个核心问题是钳位电容C1电压的控制。表2 总结了在不同电流情况下,各开关状态对电容C1电压的影响。例如当电流为正的时 候,V5和V7对C1充 电,V2和V4使C1放电,其他开关状态不影响C1的电压。根据这样的关系,按照C1的电压偏移情况和相电流的正负,可以选择合适的开关状态维持C1电压的稳定。开关状态的选择方法见表3,其中ΔU=UC−E。当ΔU 为正时,选择对C1放电的开关状态,反之选择对C1充电的开关状态,如果不存在这样的状态,则选择对C1的电压没有影响的开关状态。开关状态被分为G1和G2两组以供选择。根据这样简单的方法,就可以维持钳位电容电压的稳定。

表3 开关状态的选择 Tab.3 Selection of the switching states
对于三相对称系统,新拓扑可以采用内环辅助钳位的方法来稳定母线电容电压。该方法的提出和具体的分析在文献[19]中有详细的叙述,其母线供电结构如图16 所示。因为新拓扑中母线的中点不再有电流输出,所以相比文献[19]中的二极管钳位型五电平结构,不需要去控制内环的中点电位,控制更加简单。以母线电容电压为控制目标,构造最优函数来选择合适的开关状态,可以控制母线电容电压的稳定。同时还需要考虑控制每相钳位电容的电压,选择最优的开关状态。
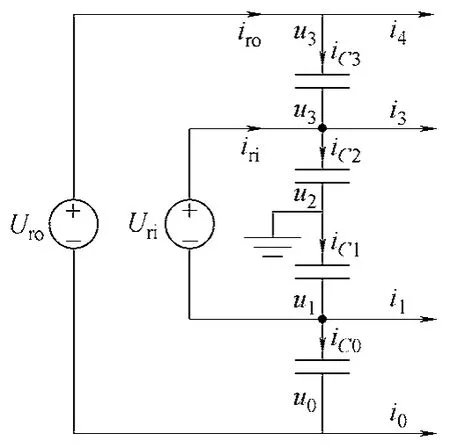
图16 内环辅助钳位结构示意图 Fig.16 Inner-loop auxiliary clamped structure
6 新拓扑的仿真研究
在新拓扑的仿真中,采用的每级电容的大小为4700μF,每级电压为500V,负载电流为10A(rms),调制系数0.8。图17 给出了开关频率为1kHz,功率因数为0.9 时刻的输出电压和电流。图18 为开关频率为1kHz,功率因数分别为0.9 和0.1 时单相结构钳位电容电压的仿真结果。可以看到通过前面所述的控制方法,钳位电容的电压能够得到很好的控制。三相系统各级母线电压和各相钳位电容电压的仿真结果如图19 所示,开关频率为1kHz,功率因数分别为0.9 和0.1。
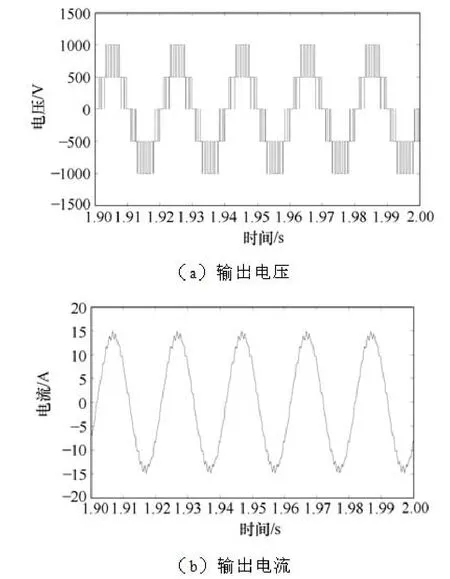
图17 开关频率1kHz,功率因数0.9 时 单相运行仿真结果 Fig.17 Simulation results of single phase leg (f=1kHz,PF=0.9)
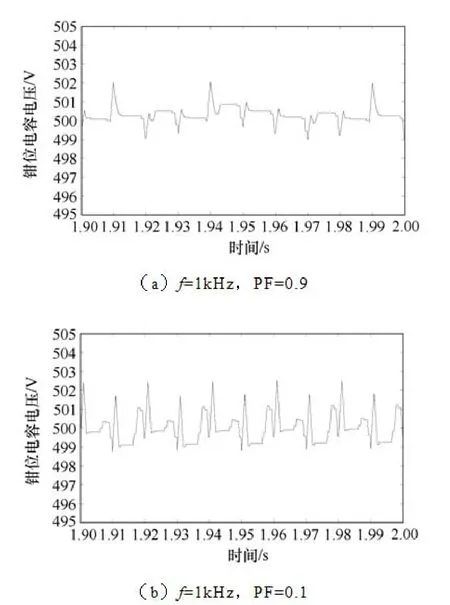
图18 单相变换器钳位电容电压仿真结果 Fig.18 Simulation results of single phase leg (voltage of the clamping capacitor)
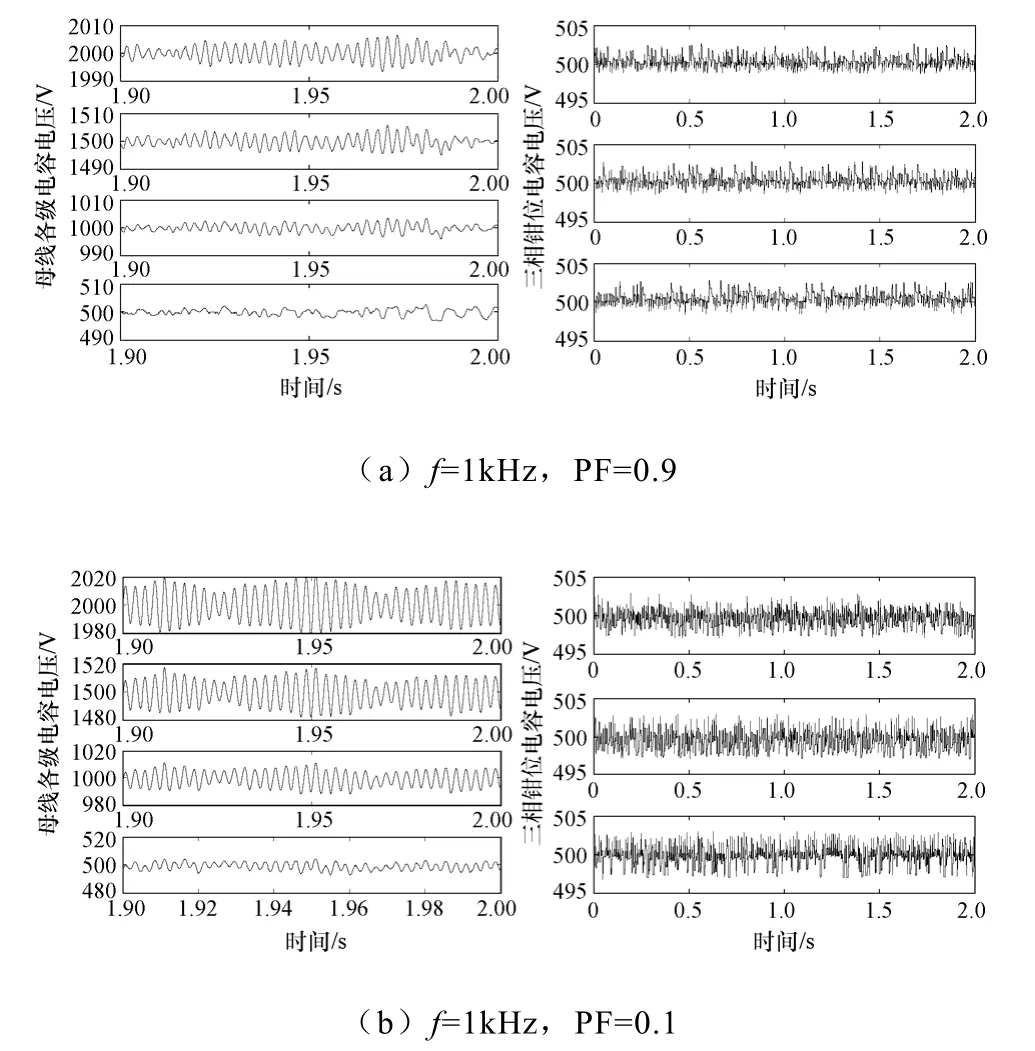
图19 三相变换器母线电压和钳位 电容电压仿真结果 Fig.19 Simulation results of three phase converter
从仿真波形可以看到,采用内环辅助钳位的方法,新拓扑结构在保持钳位电容电压稳定的同时,也能很好地控制母线各级电容的电压。
7 结论
本文从多电平基本拓扑入手,探讨了多电平拓扑结构从产生以来的发展过程,并重点分析了通用拓扑结构和其他多电平拓扑结构之间的关系,最终得到所有的多电平拓扑结构都可以从通用拓扑简化(退化)组合而来的结论,并且提出了通用多电平拓扑简化的规律。根据通用拓扑简化规律,本文提出了两种新的多电平拓扑结构,在输出相同电平数下,所用的开关器件数量最少。本文还对新拓扑的工作原理和控制方法进行了研究。通过对新拓扑的开关状态和电流通路的研究,给出了控制单相变换器的钳位电容电压稳定和三相变换器的母线各级电压稳定的方法。仿真结果也验证了所提出的多电平拓扑结构及其控制方法的正确性和可行性。
[1] Bhagwat P,Stefanovic V R.Generalized structure of a multilevel PWM inverter[J].IEEE Transactions on Industrial Applications,1983,19(6):761-766.
[2] Nabae A,Takahashi I,Akagi H.A new neutral- point-clamped PWM inverter[J].IEEE Transactions on Industrial Applications,1981,17(5):518-523.
[3] Baker R H.Bridge converter circuit:United States,4270163[P].1979.
[4] Meynard T A,Foch H,Forest F,et al.Multicell converters:derived topologies[J].IEEE Transactions on Industrial Electronics,2002,49(5):978-987.
[5] Y Xiaoming,Barbi I.Fundamentals of a new diode clamping multilevel inverter[J].IEEE Transactions on Power Electronics,2000,15(4):711-718.
[6] L Jih Sheng,P Fangzheng.Multilevel converters-a new breed of power converters[J].IEEE Transactions on Industrial Applications,1996,32(3):509-517.
[7] K Young Seok,S Beom Seok,H Dong Seok.A novel structure of multi-level high voltage source inverter[C].EPE '93,1993:132-137.
[8] Takafumi Maruyama,Kumano M.Method of controlling an inverter:United States,5155675[P].1990.
[9] Meynard T A,Foch H.Multi-level conversion:high voltage choppers and voltage-source inverters[C].PESC '92,1992:397-403.
[10] Meynard T A,Foch H,Thomas P,et al.Multicell converters:basic concepts and industry appli- cations[J].IEEE Transactions on Industrial Electronics,2002,49(5):955-964.
[11] Bruckner T,Bemet S.Loss balancing in three-level voltage source inverters applying active NPC switches[C].PESC'01,2001:1135-1140.
[12] Bruckner T,Bemet S,Guldner H.The active NPC converter and its loss-balancing control[J].IEEE Transactions on Industrial Electronics,2005,52(3):855-868.
[13] Floricau D,Gateau G,Dumitrescu M,et al.A new stacked NPC converter:3L-topology and control[C].EPE'07,2007.
[14] Gateau G,Meynard T A,Foch H.Stacked multicell converter (SMC):properties and design[C].PESC '01,2001:1583-1588.
[15] Barbosa P,Steimer P,Meysenc L,et al.Active neutral-point-clamped multilevel converters[C].PESC '05,2005:2296-2301.
[16] Haederli C,Ladoux P,Meynard T,et al.Neutral point control in multilevel converters applying novel modulation schemes[C].PESC '06,2006:1-8.
[17] Peng Fangzheng.A generalized multilevel inverter topology with self voltage balancing[J].IEEE Transactions on Industrial Applications,2001,37(2):611-618.
[18] Baker R H,Bannister L H.Electric power converter:United States,3867643[P].1974.
[19] 高跃.二极管钳位型多电平逆变器电压平衡控制的稳定域研究[D].北京:清华大学,2007.

